linalg.c File Reference

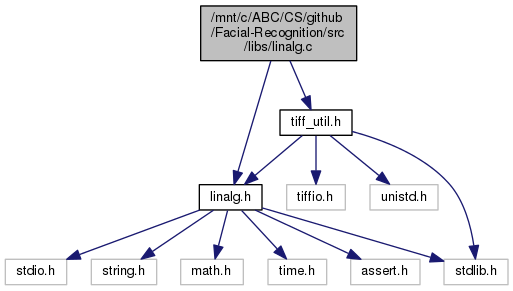
File containing common linear algebra functions. More...

#include "linalg.h"
#include "tiff_util.h"

Include dependency graph for linalg.c:

Functions
vector *	vector_create (size_t size)
	Creates a vector this function will malloc the exact space for the required dimensions. More...
matrix *	matrix_create (size_t row, size_t col)
	Creates a matrix this function will malloc the exact space for the required dimensions. More...
matrix *	vec_to_mat (vector *vec, int orientation)
	Converts vector into matrix this function will "cast" the vector into a matrix by using the fact that they both have the same size. when calling this function, calling free() on the matrix will free the vector and vice versa. More...
vector *	mat_to_vec (matrix *mat)
	Converts matrix into vector this function will "cast" the matrix into a vector by using the fact that they both have the same size. when calling this function, calling free() on the vector will free the matrix and vice versa. the input matrix can only be a matrix with dimensions 1 X N (a row matrix) More...
void	matrix_reshape (matrix *mat, size_t row, size_t col)
	Reshapes the matrix this function will reshape the matrix in constant time. More...
double	dot_product (const double *left, const double *right, int length)
	Performs dot product on two double* this function will malloc for the user a double arrays must be of same size. More...
vector *	vecscalar_multiply (const vector *vec, const double scalar)
	Performs scalar multiplication of a vector this function will malloc for the user a vector*. More...
vector *	vecscalar_divide (const vector *vec, const double scalar)
	Performs scalar division of a vector this function will malloc for the user a vector*. More...
vector *	vecmat_multiply (const vector *vec, const matrix *mat)
	Performs vector matrix multiplication this function will malloc for the user a vector* if the vector is of size M and the matrix size M by N, the resulting column vector will be of size N. More...
vector *	matvec_multiply (const matrix *mat, const vector *vec)
	Performs matrix vector multiplication this function will malloc for the user a vector* if the matrix is of size M by N and the vector N, the resulting row vector will be of size M. More...
void	mat_print (const matrix *mat)
	prints the matrix this function will not modify the matrix and print to stdout More...
void	vec_print (const vector *vec)
	prints the vector this function will not modify the vector and print to stdout More...
matrix *	matmat_multiply (const matrix *left, const matrix *right)
	Performs standard matrix multiplication this function will malloc for the user a matrix*. More...
matrix *	matmat_addition (const matrix *left, const matrix *right)
	Performs standard matrix addition this function will malloc for the user a matrix*. More...
matrix *	matmat_subtraction (const matrix *left, const matrix *right)
	Performs standard matrix subtration this function will malloc for the user a matrix*. More...
matrix *	matscalar_multiply (const matrix *mat, const double scalar)
	Performs scalar multiplication of a matrix this function will malloc for the user a matrix*. More...
matrix *	matscalar_divide (const matrix *mat, const double scalar)
	Performs scalar division of a matrix this function will malloc for the user a matrix*. More...
matrix *	mat_transpose (const matrix *mat)
	Performs matrix transpose this function will malloc for the user a matrix*. More...
void	vec_append (vector **vec_a, vector *vec_b)
	Appends vector b to vector a this function will realloc for the user vector a and free vector b. More...
void	eigen (int n, double a[], int it_max, double v[], double d[], int *it_num, int *rot_num)
	Performs Jacobi eigenvalue iteration this function will required the user to pass in non-null it_num and rot_num it does not malloc but rather requires the caller to malloc space for it. More...
void	mat_identity (int n, double a[])
	modifies a matrix to be the identity matrix of size n More...
void	diag_vector (int n, double a[], double v[])
	gets the diagonal entries More...
double	frobenius_norm (int n, int k, double a[], double x[], double lambda[])
	computes the Frobenius norm in a right eigensystem More...
matrix *	covmat (matrix *mat)
	computes the variance covariance matrix More...
vector *	compute_average (matrix *images, int num_images)
	computes the average matrix of all the *vector images More...

Detailed Description

File containing common linear algebra functions.

Minhyuk Park

Date

7 Nov 2017

Function Documentation

vector* compute_average	(	matrix *	images,
		int	num_images
	)

computes the average matrix of all the *vector images

Returns

vector* the average image

Parameters

images	matrix* a matrix where each column represents an image
num_images	int number of images in the vector

References MAT, _matrix::row, _vector::size, VEC, and vector_create().

                                                        {
    /*
    matrix* ones_row = matrix_create(1, num_images);
    for(int i =0; i <num_images; i++) {
        MAT(ones_row, 0,i) = 1;
    }
    matrix* row_images = mat_transpose(images);
    matrix* row_sum = matmat_multiply(ones_row, row_images);
    vector* vector_row_sum = mat_to_vec(row_sum);
    vector* img_avg = vecscalar_divide(vector_row_sum, num_images);
    free(vector_row_sum);
    free(row_images);
    free(ones_row);
    */
    vector* img_avg = vector_create(images->row);

    for(size_t i = 0; i < img_avg->size; i ++) {
        uint32 avg_pixel = 0;

        uint32 r = 0;
        uint32 g = 0;
        uint32 b = 0;
        uint32 a = 0;
        for(int j = 0; j < num_images; j ++) {
            uint32 current_pixel = MAT(images, i, j);

            r += ((current_pixel & 0xff) * (current_pixel & 0xff));
            g += (((current_pixel >> 8) & 0xff) * ((current_pixel >> 8) & 0xff));
            b += (((current_pixel >> 16) & 0xff) * ((current_pixel >> 16) & 0xff));
            a += (((current_pixel >> 24) & 0xff) * ((current_pixel >> 24) & 0xff));
        }

        r /= num_images;
        g /= num_images;
        b /= num_images;
        a /= num_images;

        r = sqrt(r);
        g = sqrt(g);
        b = sqrt(b);
        a = sqrt(a);
        /*
        for(int j = 0; j < num_images; j ++) {
            uint32 current_pixel = MAT(images, i, j);

            r += ((current_pixel & 0xff));
            g += (((current_pixel >> 8) & 0xff));
            b += (((current_pixel >> 16) & 0xff));
            a += (((current_pixel >> 24) & 0xff));
        }

        r /= num_images;
        g /= num_images;
        b /= num_images;
        a /= num_images;
        */


        avg_pixel |= r;
        avg_pixel |= (g << 8);
        avg_pixel |= (b << 16);
        avg_pixel |= (a << 24);

        VEC(img_avg, i) = avg_pixel;
    }


    

    return img_avg;
}

matrix* covmat

(

matrix *

mat

)

computes the variance covariance matrix

Returns

matrix* the output variance-covariance matrix this function will malloc a new matrix

Parameters

mat	a matrix* representing the input matrix of deviation scores of size n by k

References mat_transpose(), matmat_multiply(), matscalar_divide(), and _matrix::row.

                            {
    size_t n = mat->row;
    matrix* mat_T = mat_transpose(mat);
    matrix* x_T_x = matmat_multiply(mat_T, mat);
    matrix* retmat = matscalar_divide(x_T_x, n);
    free(x_T_x);
    free(mat_T);
    return retmat;
}

void diag_vector	(	int	n,
		double	a[],
		double	v[]
	)

gets the diagonal entries

Parameters

n	int the dimension
a[]	double[] input the matrix, N by N
v[]	double[] output the diagonal entries, N

Referenced by eigen().

                                                {
    for(int i = 0; i < n; i ++) {
        v[i] = a[i + i * n];
    }
    return;
}

double dot_product	(	const double *	left,
		const double *	right,
		int	length
	)

Performs dot product on two double* this function will malloc for the user a double arrays must be of same size.

Returns

a double representing the inner product

Parameters

left	const double* the first vector
right	const double* the second vector
length	int the size of the vectors

Referenced by matvec_multiply().

                                                                        {
    double retval = 0.0;
    for(int i = 0; i < length; i ++) {
        retval += (left[i] * right[i]);
    }
    return retval;
}

void eigen	(	int	N,
		double	a[],
		int	it_max,
		double	v[],
		double	d[],
		int *	it_num,
		int *	rot_num
	)

Performs Jacobi eigenvalue iteration this function will required the user to pass in non-null it_num and rot_num it does not malloc but rather requires the caller to malloc space for it.

Parameters

N	int the dimiension of the input matrix a, which is a N by N matrix
a[]	double[] the input matrix which has to be square, real, and symmetric
it_max	int maximum number of iterations to stop at
v[]	double[]output matrix of eigenvectors, which is a N by N matrix
d[]	double[] output matrix of eigenvalues, in descending order
it_num	int* output total number of iterations
rot_num	int* output total number of rotations

References diag_vector(), and mat_identity().

                                                                                             {
    mat_identity(n, v); // create the identity matrix using what the caller allocated for us
    diag_vector(n, a, d); // get the diagonal values of a and store it in caller allocated vector d

    double* bw = (double*) malloc(n * sizeof(double));
    double* zw = (double*) malloc(n * sizeof(double));

    for(int i = 0; i < n; i ++) {
        bw[i] = d[i];
        zw[i] = 0.0;
    }
    *it_num = 0;
    *rot_num = 0;

    double thresh = 0.0;
    double gapq = 0.0;
    while(*it_num < it_max) {
        *it_num += 1;
        thresh = 0.0;
        // set up the convergence threshold
        // based on the size of strict upper triangle
        for(int i = 0; i < n; i ++) {
            for(int j = 0; j < i; j ++) {
                thresh += (a[j + i * n] * a[j + i * n]);
            }
        }
        // PASS 1
        thresh = sqrt(thresh) / (double)(4 * n);
        if(thresh == 0.0) {
            break;
        }
        // PASS 2
        for(int p = 0; p < n; p ++) {
            for(int q = p + 1; q < n; q ++) {
                gapq = 10.0 * fabs(a[p + q * n]);
                double termp = gapq + fabs(d[p]);
                double termq = gapq + fabs(d[q]);
                if(4 < *it_num && termp == fabs(d[p]) && termq == fabs(d[q])) {
                    a[p + q * n] = 0.0;
                // apply rotation otherwise
                // PASS 3
                } else if(thresh <= fabs(a[p + q * n])) {
                    double h = d[q] - d[p];
                    double term = fabs(h) + gapq;
                    double t = 0.0;
                    if(term == fabs(h)) {
                        t = a[p + q * n] / h;
                    } else {
                        double theta = 0.5 * h / a[p + q * n];
                        t = 1.0 / (fabs(theta) + sqrt(1.0 + theta * theta));
                        if(theta < 0.0) {
                            t = -t;
                        }
                    }
                    // PASS 4
                    double c = 1.0 / sqrt(1.0 + t * t);
                    double s = t * c;
                    double tau = s / (1.0 + c);
                    h = t * a[p + q * n];

                    zw[p] -= h;
                    zw[q] += h;
                    d[p] -= h;
                    d[q] += h;
                    a[p + q * n] = 0.0;
                    // PASS 5
                    // rotate
                    double g = 0.0;
                    for(int j = 0; j < p; j ++) {
                        g = a[j + p * n];
                        h = a[j + q * n];
                        a[j + p * n] = g - s * (h + g * tau);
                        a[j + q * n] = h + s * (g - h * tau);
                    }
                    for(int j = p + 1; j < q; j ++) {
                        g = a[p + j * n];
                        h = a[j + q * n];
                        a[p + j * n] = g - s * (h + g * tau);
                        a[j + q * n] = h + s * (g - h * tau);
                    }
                    for(int j = q + 1; j < n; j ++) {
                        g = a[p + j * n];
                        h = a[q + j * n];
                        a[p + j * n] = g - s * (h + g * tau);
                        a[q + j * n] = h + s * (g - h * tau);
                    }
                    // PASS 6
                    // store to eigenvector matrix v
                    for(int j = 0; j < n; j ++) {
                        g = v[j + p * n];
                        h = v[j + q * n];
                        v[j + p * n] = g - s * (h + g * tau);
                        v[j + q * n] = h + s * (g - h * tau);
                    }
                    *rot_num += 1;
                }
            }
        }
        for(int i = 0; i < n; i ++) {
            bw[i] += zw[i];
            d[i] = bw[i];
            zw[i] = 0.0;
        }
    }
    // PASS 7
    // restore upper triangle
    for(int i = 0; i < n; i ++) {
        for(int j = 0; j < i; j ++) {
            a[j + i * n] = a [i + j * n];
        }
    }
    for(int k = 0; k < n - 1; k ++) {
        int m = k;
        for(int l = k + 1; l < n; l ++) {
            if(d[l] < d[m]) {
                m = l;
            }
        }
        if(m != k) {
            double t = d[m];
            d[m] = d[k];
            d[k] = t;
            for(int i = 0; i < n; i ++) {
                double w = v[i + m * n];
                v[i + m * n] = v[i + k * n];
                v[i + k * n] = w;
            }
        }
    }
    free(bw);
    free(zw);
    return;
}

double frobenius_norm	(	int	n,
		int	k,
		double	a[],
		double	x[],
		double	lambda[]
	)

computes the Frobenius norm in a right eigensystem

Returns

double the frobenius norm of A * X - X * lambda

Parameters

n	int the dimension of the matrix
k	int the number of eigen vectors
a[]	double[] input matrix of size n by n
x[]	double[] input vector of eigenvectors of size k
lamdba[]	double[] input vector of eigen values

                                                                             {
    double* c = (double*) malloc(n * k * sizeof(double));
    for(int i = 0; i < k; i ++) {
        for(int j = 0; j < n; j ++) {
            c[j + i * n] = 0.0;
            for(int l = 0; l < n; l ++) {
                c[j + i * n] = c[j + i * n] + a[j + l * n] * x[l + i * n];
            }
        }
    }
    for(int i = 0; i < k; i ++) {
        for(int j = 0; j < n; j ++) {
            c[j + i * n] = c[j + i * n] - lambda[i] * x[j + i * n];
        }
    }
    double retval = 0.0;
    for(int i = 0; i < k; i ++) {
        for(int j = 0; j < n; j ++) {
            retval += pow(c[j + i * n], 2);
        }
    }
    retval = sqrt(retval);
    free(c);
    return retval;
}

void mat_identity	(	int	n,
		double	a[]
	)

modifies a matrix to be the identity matrix of size n

Parameters

n	int the dimension
a[]	double output identity matrix

Referenced by eigen().

                                     {
    int k = 0;
    for (int j = 0; j < n; j ++ ) {
        for (int i = 0; i < n; i ++ ) {
            if ( i == j ) {
                a[k] = 1.0;
            } else {
                a[k] = 0.0;
            }
            k += 1;
        }
    }
    return;
}

void mat_print

(

const matrix *

mat

)

prints the matrix this function will not modify the matrix and print to stdout

Parameters

mat	const matrix* the matrix to be printed

References _matrix::col, MAT, and _matrix::row.

                                  {
    for(size_t i = 0; i < mat->row; i ++) {
        for(size_t j = 0; j < mat->col; j ++) {
            if(j == mat->col - 1) {
                printf("%f ", MAT(mat, i, j));                
            } else {
                printf("%f, ", MAT(mat, i, j));
            }
        }
        printf("\n");
    }
}

vector* mat_to_vec

(

matrix *

mat

)

Converts matrix into vector this function will "cast" the matrix into a vector by using the fact that they both have the same size. when calling this function, calling free() on the vector will free the matrix and vice versa. the input matrix can only be a matrix with dimensions 1 X N (a row matrix)

Returns

vector* the new pointer for input matrix*

Parameters

mat	matrix* to be converted in terms of the newly formed vector

References _matrix::col, and _matrix::row.

                                {
    assert(mat->row = 1);
    mat->row = mat->col;
    mat->col = 1;
    return (vector*)mat;
}

matrix* mat_transpose

(

const matrix *

mat

)

Performs matrix transpose this function will malloc for the user a matrix*.

Returns

matrix* the newly transposed and malloced matrix

Parameters

mat	const matrix* the matrix to be transposed

References _matrix::col, MAT, matrix_create(), and _matrix::row.

Referenced by covmat().

                                         {
    matrix* retval = matrix_create(mat->col, mat->row);
    for (size_t i = 0; i < mat->row; i ++) {
        for (size_t j = 0; j < mat->col; j ++) {
            MAT(retval, j, i) = MAT(mat, i, j);
        }
    }
    return retval;
}

matrix* matmat_addition	(	const matrix *	left,
		const matrix *	right
	)

Performs standard matrix addition this function will malloc for the user a matrix*.

Returns

matrix* newly malloced result of left plus right

Parameters

left	const matrix* the matrix to be added to
right	const matrix* the matrix to be added

References _matrix::col, MAT, matrix_create(), and _matrix::row.

                                                                 {
    matrix* retval = matrix_create(left->row, right->col);
    for (size_t i = 0; i < left->row; i ++) {
       for (size_t j = 0; j < right->col; j ++) {
            MAT(retval, i, j) = MAT(left, i, j) + MAT(right, i, j);
        }
    }
    return retval;
}

matrix* matmat_multiply	(	const matrix *	left,
		const matrix *	right
	)

Performs standard matrix multiplication this function will malloc for the user a matrix*.

Returns

matrix* newly malloced result of left times right

Parameters

left	const matrix* the matrix to be multiplied to
right	const matrix* the matrix to be multiplied

References _matrix::col, MAT, matrix_create(), and _matrix::row.

Referenced by covmat().

                                                                 {
    matrix* retval = matrix_create(left->row, right->col);
    for(size_t i = 0; i < left->row; i ++) {
        for(size_t j = 0; j < right->col; j ++) {
            MAT(retval,i,j) = 0;
            for(size_t k = 0; k < left->col; k ++) {
                MAT(retval, i, j) += MAT(left, i, k) * MAT(right, k, j);
            }
        }
    }   
    return retval;
}

matrix* matmat_subtraction	(	const matrix *	left,
		const matrix *	right
	)

Performs standard matrix subtration this function will malloc for the user a matrix*.

Returns

matrix* newly malloced result of left minus right

Parameters

left	const matrix* the matrix to be subtracted from
right	const matrix* the matrix to be subtrated

References _matrix::col, MAT, matrix_create(), and _matrix::row.

                                                                    {
    matrix* retval = matrix_create(left->row, right->col);
    for (size_t i = 0; i < left->row; i ++) {
        for (size_t j = 0; j < right->col; j ++) {
            MAT(retval, i, j) = MAT(left, i, j) - MAT(right, i, j);
        }
    }
    return retval;
}

matrix* matrix_create	(	size_t	row,
		size_t	col
	)

Creates a matrix this function will malloc the exact space for the required dimensions.

Returns

matrix* the newly malloced matrix

Parameters

row	size_t the desired number of rows in the matrix
col	size_t the desired number of columns in the matrix

References _matrix::col, and _matrix::row.

Referenced by mat_transpose(), matmat_addition(), matmat_multiply(), matmat_subtraction(), and matscalar_multiply().

                                              {
    if(row <= 0 || col <= 0) {
        return NULL;
    }
    matrix* retval =  malloc((row * col * sizeof(double)) + (2 * sizeof(size_t)));
    retval->row = row;
    retval->col = col;
    return retval;
}

void matrix_reshape	(	matrix *	mat,
		size_t	row,
		size_t	col
	)

Reshapes the matrix this function will reshape the matrix in constant time.

Parameters

mat	matrix* to be reshaped
row	size_t the new row
col	size_t the new column

References _matrix::col, and _matrix::row.

                                                         {
    mat->row = row;
    mat->col = col;
}

matrix* matscalar_divide	(	const matrix *	mat,
		const double	scalar
	)

Performs scalar division of a matrix this function will malloc for the user a matrix*.

Returns

matrix* that is the result of element wise division of the matrix by the scalar

Parameters

mat	const matrix* the input matrix
scalar	const double the input scalar

References matscalar_multiply().

Referenced by covmat().

                                                                 {
    return matscalar_multiply(mat, 1/scalar);
}

matrix* matscalar_multiply	(	const matrix *	mat,
		const double	scalar
	)

Performs scalar multiplication of a matrix this function will malloc for the user a matrix*.

Returns

matrix* that is the result of element wise multiplication of the matrix by the scalar

Parameters

mat	const matrix* the input matrix
scalar	const double the input scalar

References _matrix::col, MAT, matrix_create(), and _matrix::row.

Referenced by matscalar_divide().

                                                                   {
    matrix* retval = matrix_create(mat->row, mat->col);
    for (size_t i = 0; i < mat->row; i++) {
        for (size_t j = 0; j < mat->col; j++) {
            MAT(retval,i,j) = MAT(mat,i,j) * scalar;
        }
    }
    return retval;
}

vector* matvec_multiply	(	const matrix *	mat,
		const vector *	vec
	)

Performs matrix vector multiplication this function will malloc for the user a vector* if the matrix is of size M by N and the vector N, the resulting row vector will be of size M.

Returns

vector* newly malloced result of matrix vector multiplication

Parameters

mat	const matrix* the input matrix
vec	const vector* the input vector

References _matrix::col, _vector::data, _matrix::data, dot_product(), _vector::size, VEC, and vector_create().

                                                              {
    if(vec == NULL  || mat == NULL) {
        return NULL;
    }
    vector* retval = vector_create(vec->size);
    for(size_t i = 0; i < retval->size; i++) { 
        VEC(retval,i) = dot_product(((double*)(mat->data) + (mat->col * i)), (double*)vec->data, vec->size);
    }
    return retval;
}

void vec_append	(	vector **	vec_a,
		vector *	vec_b
	)

Appends vector b to vector a this function will realloc for the user vector a and free vector b.

Parameters

vec_a	vector** the vector to be realloced
vec_b	vector* the vector to be appended and freed thereafter

References _vector::data, _vector::size, and vector_create().

Referenced by tiff_stream_to_vec().

{
    void* saved_vec_a = *vec_a;
    vector* buffer = vector_create(vec_b->size);
    memcpy(buffer, vec_b, sizeof(double) * vec_b->size + (2 * sizeof(size_t)));
    size_t newSize = (*vec_a)->size + buffer->size;
    void* dest = *vec_a;
    void* arrv = NULL;
    arrv = realloc(dest, sizeof(double) * newSize + (2 * sizeof(size_t)));
    *vec_a = arrv;    
    memcpy((*vec_a)->data + (*vec_a)->size, buffer->data, buffer->size *sizeof(double));
    (*vec_a)->size = newSize;
    free(buffer);
    if(saved_vec_a != vec_b)
    {
        free(vec_b);
    }
}

void vec_print

(

const vector *

vec

)

prints the vector this function will not modify the vector and print to stdout

Parameters

vec	const vector* the vector to be printed

References _vector::data, and _vector::size.

                                  {
    for(size_t i = 0; i < vec->size; i ++) {
        printf("%f ", vec->data[i]);
    }
    printf("\n");
}

matrix* vec_to_mat	(	vector *	vec,
		int	orientation
	)

Converts vector into matrix this function will "cast" the vector into a matrix by using the fact that they both have the same size. when calling this function, calling free() on the matrix will free the vector and vice versa.

Returns

matrix* the new pointer for input vector*

Parameters

vec	vector* to be converted
orientation	int 1 is Row-wise and 0 is Column-wise in terms of the newly formed matrix

References _vector::padding, and _vector::size.

                                                 {
    if(orientation == 1) {
        vec->padding = vec->size;
        vec->size = 1;
    } else {
        vec->padding = 1;
    }
    return (matrix*)vec;
}

vector* vecmat_multiply	(	const vector *	vec,
		const matrix *	mat
	)

Performs vector matrix multiplication this function will malloc for the user a vector* if the vector is of size M and the matrix size M by N, the resulting column vector will be of size N.

Returns

vector* newly malloced result of vector matrix multiplication

Parameters

vec	const vector* the input vector
mat	const matrix* the input matrix

References _matrix::col, _vector::data, MAT, _matrix::row, _vector::size, VEC, and vector_create().

                                                               {
    if(vec == NULL  || mat == NULL) {
        return NULL;
    }
    vector* retval = vector_create(vec->size);
    memset(retval->data, 0, sizeof(double) * vec->size);
    for(size_t j = 0; j < mat->col; j ++) {
        for(size_t i = 0; i < mat->row; i ++) {
            VEC(retval, j) += (VEC(vec, i) * MAT(mat, i, j));
        }
    }
    return retval;
}

vector* vecscalar_divide	(	const vector *	vec,
		const double	scalar
	)

Performs scalar division of a vector this function will malloc for the user a vector*.

Returns

vector* that is the result of element wise division of the vector by the scalar

Parameters

vec	const vector* the input vector
scalar	const double the input scalar

References vecscalar_multiply().

                                                                 {
    return vecscalar_multiply(vec, 1 / scalar);
}

vector* vecscalar_multiply	(	const vector *	vec,
		const double	scalar
	)

Performs scalar multiplication of a vector this function will malloc for the user a vector*.

Returns

vector* that is the result of element wise multiplication of the vector by the scalar

Parameters

vec	const vector* the input vector
scalar	const double the input scalar

References _vector::size, VEC, and vector_create().

Referenced by vecscalar_divide().

                                                                   {
    vector* retval = vector_create(vec->size);
    for (size_t i = 0; i < retval->size; i ++) {
        VEC(retval, i) = VEC(vec, i) * scalar;
    }
    return retval; 
}

vector* vector_create

(

size_t

size

)

Creates a vector this function will malloc the exact space for the required dimensions.

Returns

vector* the newly malloced vector

Parameters

size	size_t the desired number of elements in the vecrtor

References _vector::padding, and _vector::size.

Referenced by compute_average(), matvec_multiply(), tiff_to_vec(), vec_append(), vecmat_multiply(), and vecscalar_multiply().

                                   {
    if(size <= 0) {
        return NULL;
    }
    vector* retval = malloc((size * sizeof(double)) + (2 * sizeof(size_t)));
    retval->size = size;
    retval->padding  = 0;
    return retval;
}