Die Idee der Fehlerkorrektur

				In dem Beispiel auf der letzten Seite haben wir gesehen, daß dvdisaster die Daten aus den noch lesbaren Teilen des defekten Datenträgers und den Fehlerkorrektur-Daten wiederherstellt. Ein grundlegendes Verständnis der Fehlerkorrektur ist auf jeden Fall hilfreich, um dvdisaster nutzbringend einzusetzen. Bei der Gelegenheit können wir mit der ab und zu gemachten Vermutung aufräumen, daß die Fehlerkorrektur-Daten nur eine Kopie der letzten 20% des Datenträgers seien. So einfach geht es nun auch wieder nicht ;-)
80%		20%

Beispiel: Annas Schreibtisch-PIN

Anna besitzt einen Schreibtisch, dessen Schubladen nur aufgehen, wenn man die Zahlenkombination "8 6 2 3" eingibt. Da die Schubladen keinen wertvollen Inhalt enthalten, beschließt Anna die Zahlenkombination auf dem Schreibtisch zu notieren:

Allerdings befürchtet sie, daß eine der Zahlen durch einen Tintenfleck unlesbar werden könnte. Daher schreibt sie zusätzlich noch die Summe der vier Zahlen dazu ("+" und "=" - Zeichen sind nur zur Verdeutlichung dazugeschrieben):

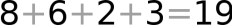
Nach einer Weile wird tatsächlich eine Zahl durch einen Tintenfleck verdeckt:

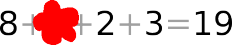
Das ist aber kein Problem, da Anna sich die fehlende Zahl x durch Umstellen der Gleichung wieder ausrechnen kann:

8 + x + 2 + 3 = 19, also

x = 19 - 8 - 2 - 3, demnach ist x = 6.

Man kann sich leicht davon überzeugen, daß auf diese Weise jede Zahl aus den anderen vier Zahlen wieder berechnet werden kann. Das Rechenbeispiel verdeutlicht außerdem die grundlegenden Eigenschaften der Fehlerkorrektur:

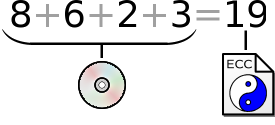Zu einer gegebenen Menge von Daten (hier die Zahlenfolge "8 6 2 3") kann man zusätzliche Fehlerkorrektur-Daten berechnen (hier die Summe "19"), mit denen sich verlorengegangene Daten wieder errechnen lassen. Bei dvdisaster ist es ganz ähnlich; hier ist die zu schützende Zahlenfolge nichts anderes als das ISO-Abbild einer CD, DVD oder BD.

Der Begriff der Redundanz läßt sich damit wie folgt erklären:

• Zu 4 Eingabezahlen wird eine weitere "Fehlerkorrektur-Zahl" berechnet. 1 von 4 (oder 1/4) entspricht einer Redundanz von 25%.
• Aus der Fehlerkorrektur-Zahl kann eine andere Zahl wieder berechnet werden, also höchstens 25% der Daten. Die Kapazität der Fehlerkorrektur entspricht der Redundanz.
• Der zusätzliche Speicherverbrauch durch die Fehlerkorrektur-Daten entspricht ebenfalls der gewählten Redundanz, also 25%

• keine Daten wiederhergestellt werden können, wenn der Datenverlust größer als die Redundanz ist (für zwei oder mehr fehlende Zahlen kann die Gleichung nicht eindeutig gelöst werden).
• die Fehlerkorrektur-Daten berechnet werden müssen, wenn noch alle Daten vorhanden sind.

Das hier gezeigte Summenbeispiel läßt sich allerdings nicht zur einer Fehlerkorrektur verallgemeinern, die mehr als einen fehlenden Datenwert korrigieren kann. Dazu braucht man ein mächtigeres Gleichungssystem, das sich auch für mehrere fehlende Werte (= Variablen) eindeutig lösen läßt. Der in dvdisaster verwendete Reed-Solomon-Kode hat diese Eigenschaften; er ist jedoch mit der üblichen Schulmathematik nicht anschaulich zu erklären. Daher mögen an weiterführenden Informationen interessierte Leser die entsprechende Literatur aus der Kodierungstheorie hinzuziehen.