MASH v FLASH detailed simulation study
Last updated: 2018-07-22
workflowr checks: (Click a bullet for more information)-
✔ R Markdown file: up-to-date
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
-
✔ Environment: empty
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
-
✔ Seed:
set.seed(20180609)The command
set.seed(20180609)was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible. -
✔ Session information: recorded
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
-
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.✔ Repository version: 3abd505
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can usewflow_publishorwflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.Ignored files: Ignored: .DS_Store Ignored: .Rhistory Ignored: .Rproj.user/ Ignored: docs/.DS_Store Ignored: docs/images/.DS_Store Ignored: output/.DS_Store Unstaged changes: Modified: code/gtex2.R Modified: code/sims2.R Modified: output/README.md Modified: output/gtex2flfit.rds Modified: output/gtex2lfsr.rds Modified: output/gtex2mfit.rds Modified: output/gtex2mrandfit.rds Modified: output/gtexrandomfit.rds Modified: output/gtexstrongfit.rds
Expand here to see past versions:
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | 3abd505 | Jason Willwerscheid | 2018-07-22 | wflow_publish(c(“analysis/MASHvFLASHsims.Rmd”, |
| html | 0a83e6c | Jason Willwerscheid | 2018-07-22 | Build site. |
| Rmd | 044fb97 | Jason Willwerscheid | 2018-07-22 | wflow_publish(“analysis/MASHvFLASHsims2.Rmd”) |
| html | 8720e9c | Jason Willwerscheid | 2018-07-01 | Build site. |
| Rmd | 1874a0d | Jason Willwerscheid | 2018-07-01 | wflow_publish(c(“analysis/MASHvFLASHgtex2.Rmd”, |
| html | 00ac712 | Jason Willwerscheid | 2018-06-26 | Build site. |
| Rmd | 81adb8c | Jason Willwerscheid | 2018-06-26 | wflow_publish(“analysis/MASHvFLASHsims2.Rmd”) |
| html | ce6e790 | Jason Willwerscheid | 2018-06-26 | Build site. |
| Rmd | 5d62591 | Jason Willwerscheid | 2018-06-26 | wflow_publish(“analysis/MASHvFLASHsims2.Rmd”) |
| html | e875bf9 | Jason Willwerscheid | 2018-06-24 | Build site. |
| Rmd | 7e4bbe0 | Jason Willwerscheid | 2018-06-24 | wflow_publish(c(“analysis/MASHvFLASHsims2.Rmd”)) |
| html | 97fa87c | Jason Willwerscheid | 2018-06-24 | Build site. |
| Rmd | 42cd89c | Jason Willwerscheid | 2018-06-24 | wflow_publish(c(“analysis/MASHvFLASHsims2.Rmd”, |
| html | 17ae3f3 | Jason Willwerscheid | 2018-06-24 | Build site. |
| Rmd | 411c3b4 | Jason Willwerscheid | 2018-06-24 | wflow_publish(“analysis/MASHvFLASHsims2.Rmd”) |
Introduction
Here I study in detail simulations from a MASH model that extends the “model with independent, unique, and shared effects” from my larger simulation study. I run 10 simulations, each of which simulates data for 20 conditions and 1200 tests. I use 17 different covariance structures, each of which are used to simulate 25 tests. The other 775 tests are null across all conditions. For the code used in this analysis, see below.
Independent effects
Effects were nonnull for all conditions and generated independently from a \(N(0, \sigma^2)\) distribution. I simulated \((1)\) small independent effects (\(\sigma^2 = 2^2\)), \((2)\) large independent effects (\(\sigma^2 = 5^2\)), and \((3)\) independent effects of varying sizes (with \(\sigma^2\) ranging from \(1^2\) to \(5^2\)).
Notice that cases 1 and 2 are covered by “canonical” covariance matrices in MASH, but 3 is not.
Identical effects
Effects were nonnull for all conditions, with an effect size that was identical across conditions. The unique effect size was generated from a \(N(0, \sigma^2)\) distribution. Similar to the above, I simulated \((4)\) small identical effects (\(\sigma^2 = 2^2\)) and \((5)\) large identical effects (\(\sigma^2 = 5^2\)).
Both of these cases are covered by canonical covariance matrices in MASH.
Rank-one effects
These are similar to “identical effects” in that the covariance matrix has rank one (so that conditions 2-20 are always fixed multiples of condition 1), but here, the effect sizes vary.
\((6)\) The effect size for condition 1 was generated from a \(N(0, 1)\) distribution, and conditions 1-20 were multiples evenly spaced between 1 and 5.
Unlike identical effects, rank-one effects are not directly modeled by canonical covariance matrices.
Unique effects
Effects were nonnull in one condition only, with the nonnull effect simulated from a \(N(0, \sigma^2)\) distribution. I simulated \((7)\) small effects (\(\sigma^2 = 3^2\)) unique to condition 1 and \((8)\) large effects (\(\sigma^2 = 8^2\)) unique to condition 2.
These effects are directly modeled by canonical covariance matrices.
Random covariance
I included three random covariance structures in which effects were nonnull across all conditions. In each case the random covariance matrix \(A^T A\) was generated by sampling the entries of \(A\) independently from a \(N(0, 2^2)\) distribution. I included \((12)\) a rank-5 random covariance matrix (with \(A \in \mathbb{R}^{5 \times 44}\)), \((13)\) a rank-10 random covariance matrix \((A \in \mathbb{R}^{10 \times 44})\), and \((14)\) a full-rank random covariance matrix \((A \in \mathbb{R}^{44 \times 44})\).
Combinations of independent, identical, and unique effects
Finally, I included several combinations of the above types of effects. In particular, I simulated \((15)\) small identical effects (covariance type 4) plus large independent effects (type 2), \((16)\) small independent effects (type 1) plus a large unique effect (type 8), and \((17)\) small identical effects (type 4) plus a large unique effect (type 8).
Fitting methods
For each simulation, I fitted a MASH model and two FLASH models using the “one-hots last” method described in my larger simulation study. One FLASH model used the point-normal approach to solve the ebnm problem (ebnm_fn = ebnm_pn); the other used ashr (ebnm_fn = ebnm_ash).
First I load results.
all.rrmses <- sqrt(readRDS("./output/sims2mse.rds"))
pr.pn <- readRDS("./output/sims2prpn.rds")
pr.ash <- readRDS("./output/sims2prash.rds")
pr.m <- readRDS("./output/sims2prm.rds")
# Nulls
nullidx <- c(7, 9, 11, 13, 15, 23)
null.names <- c("UnSm(7)", "UnLg(8)", "Sh3(9)", "Sh10(10)", "Sh5(11)", "Null")
# Effects that are independent or identical across conditions
indididx <- 1:6
indid.names <- c("IndSm(1)", "IndLg(2)", "IndDif(3)", "IdSm(4)", "IdLg(5)", "Rnk1(6)")
# Effects that are unique to one or several conditions
unshidx <- c(8, 10, 12, 14, 16)
unsh.names <- c("UnSm(7)", "UnLg(8)", "Sh3(9)", "Sh10(10)", "Sh5(11)")
# Other
otheridx <- c(17:22)
other.names <- c("Rn5(12)", "Rn10(13)", "Rnd(14)", "IdIn(15)", "InUn(16)", "IdUn(17)")Results: RRMSE
Here I give a detailed breakdown of the relative root mean-squared errors (that is, the RMSE for each fit object, divided by the RMSE that would be obtained by simply using the observed data \(Y\) to estimate the “true effects” \(X\)). In addition to calculating the RRMSE separately for each covariance type, I also separately consider null effects and nonnull effects.
MASH does much better in shrinking null effects towards zero, particularly for tests that are null across all conditions or that are unique to a single condition (covariance types 7-8). MASH also does consistently better in estimating nonnull effects when effects are independent across conditions (types 1-3). (In such cases, FLASH does worse than the naive estimate \(\hat{X} = Y\).)
Results for other covariance types are more varied: MASH appears to do better on identical effects (types 4-5, whose covariance structures are included as “canonical”), but slightly worse on rank-one effects (type 6, which is not accounted for by canonical covariance matrices). FLASH seems to outperform MASH on shared effects (types 9-11), but (somewhat surprisingly) MASH does better on random covariance matrices and on combinations involving independent effects (types 12-16), with an RRMSE near 1 (whereas FLASH is again outperformed by the naive estimate \(\hat{X} = Y\)). Finally, FLASH does much better on a combination of identical and unique effects (type 17).
In general, the ash fits perform very similarly to the point-normal fits.
RRMSE for null effects is as follows (where “null” below refers to tests that are null across all conditions):
par(mar = c(5,4,4,6))
legend.names <- c("FL-pn", "FL-ash", "MASH")
legend.args <- list(x="right", bty="n", inset=c(-0.25,0), xpd=T)
barplot(all.rrmses[,nullidx], names.arg = null.names, beside=T,
ylim=c(0, 1), ylab="RRMSE", main="RRMSE for null effects",
legend.text=legend.names, args.legend=legend.args)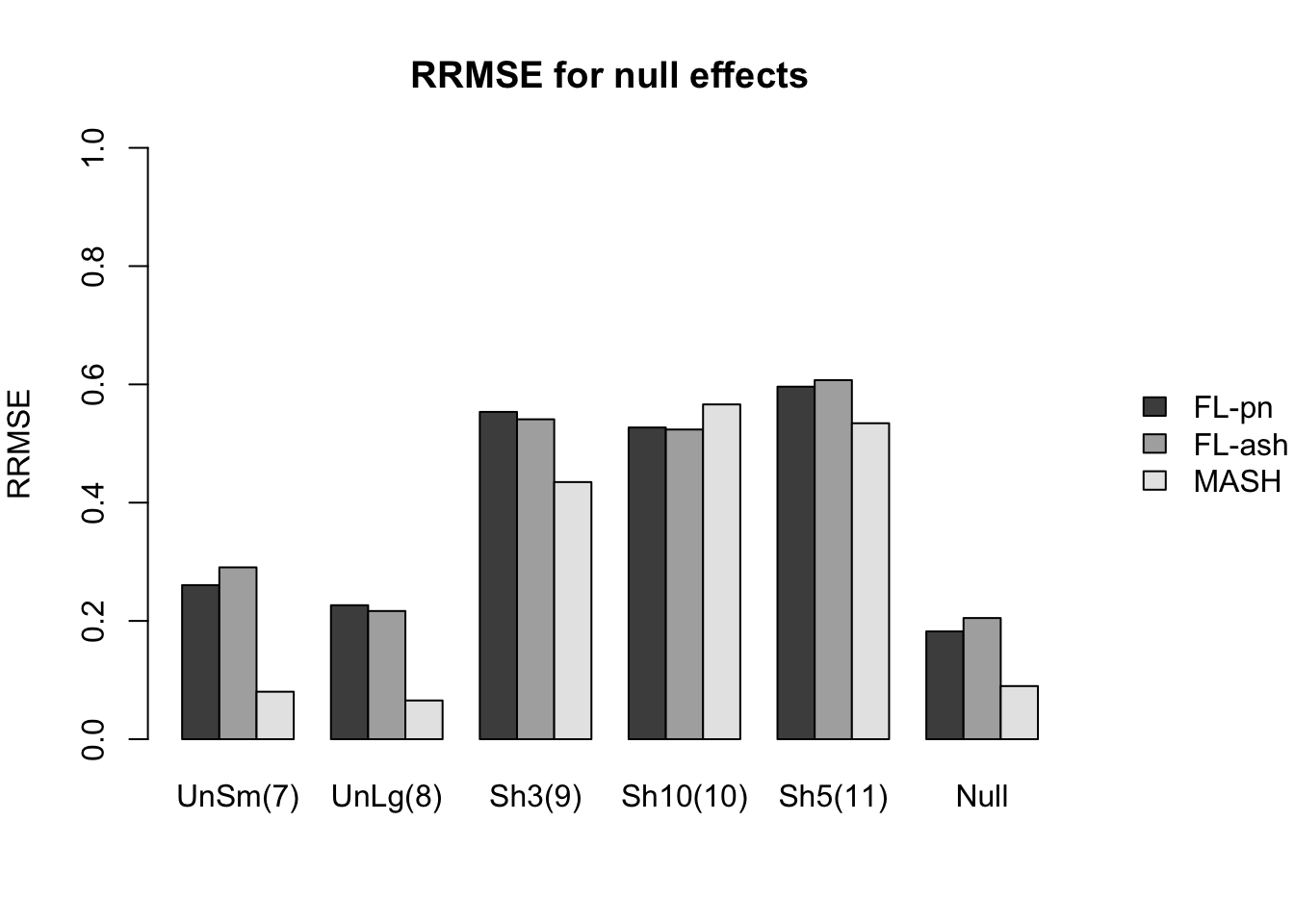
Expand here to see past versions of mse_null-1.png:
| Version | Author | Date |
|---|---|---|
| 0a83e6c | Jason Willwerscheid | 2018-07-22 |
| ce6e790 | Jason Willwerscheid | 2018-06-26 |
| 17ae3f3 | Jason Willwerscheid | 2018-06-24 |
And RRMSE for nonnull effects is as follows.
par(mar = c(5,4,4,6))
barplot(all.rrmses[,indididx], names.arg = indid.names, beside=T,
ylim=c(0, 2), ylab="RRMSE", main="RRMSE for nonnull effects",
legend.text=legend.names, args.legend=legend.args)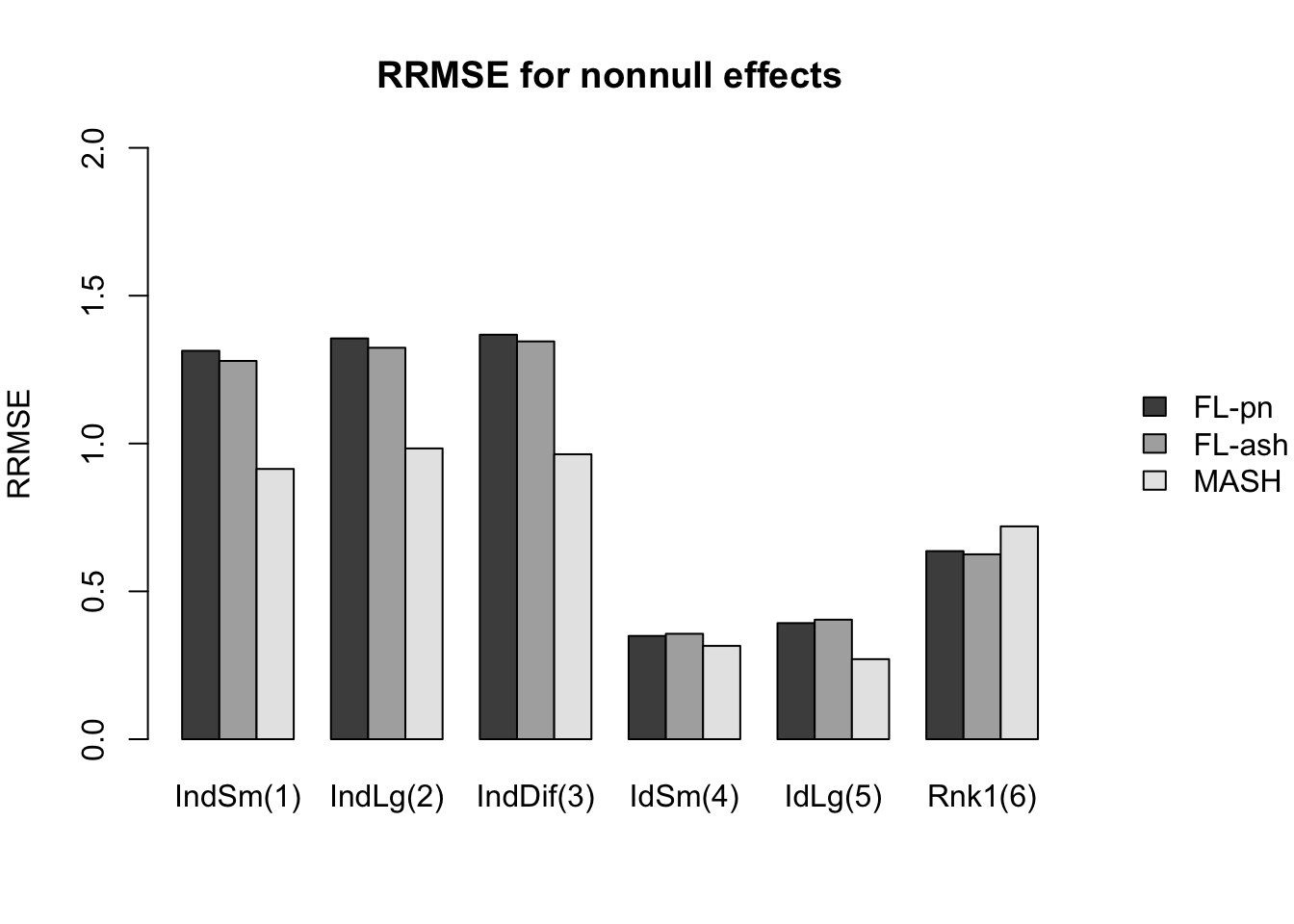
Expand here to see past versions of mse_nonnull-1.png:
| Version | Author | Date |
|---|---|---|
| 0a83e6c | Jason Willwerscheid | 2018-07-22 |
| ce6e790 | Jason Willwerscheid | 2018-06-26 |
| 17ae3f3 | Jason Willwerscheid | 2018-06-24 |
barplot(all.rrmses[,unshidx], names.arg = unsh.names, beside=T,
ylim=c(0, 2), ylab="RRMSE", main="",
legend.text=legend.names, args.legend=legend.args)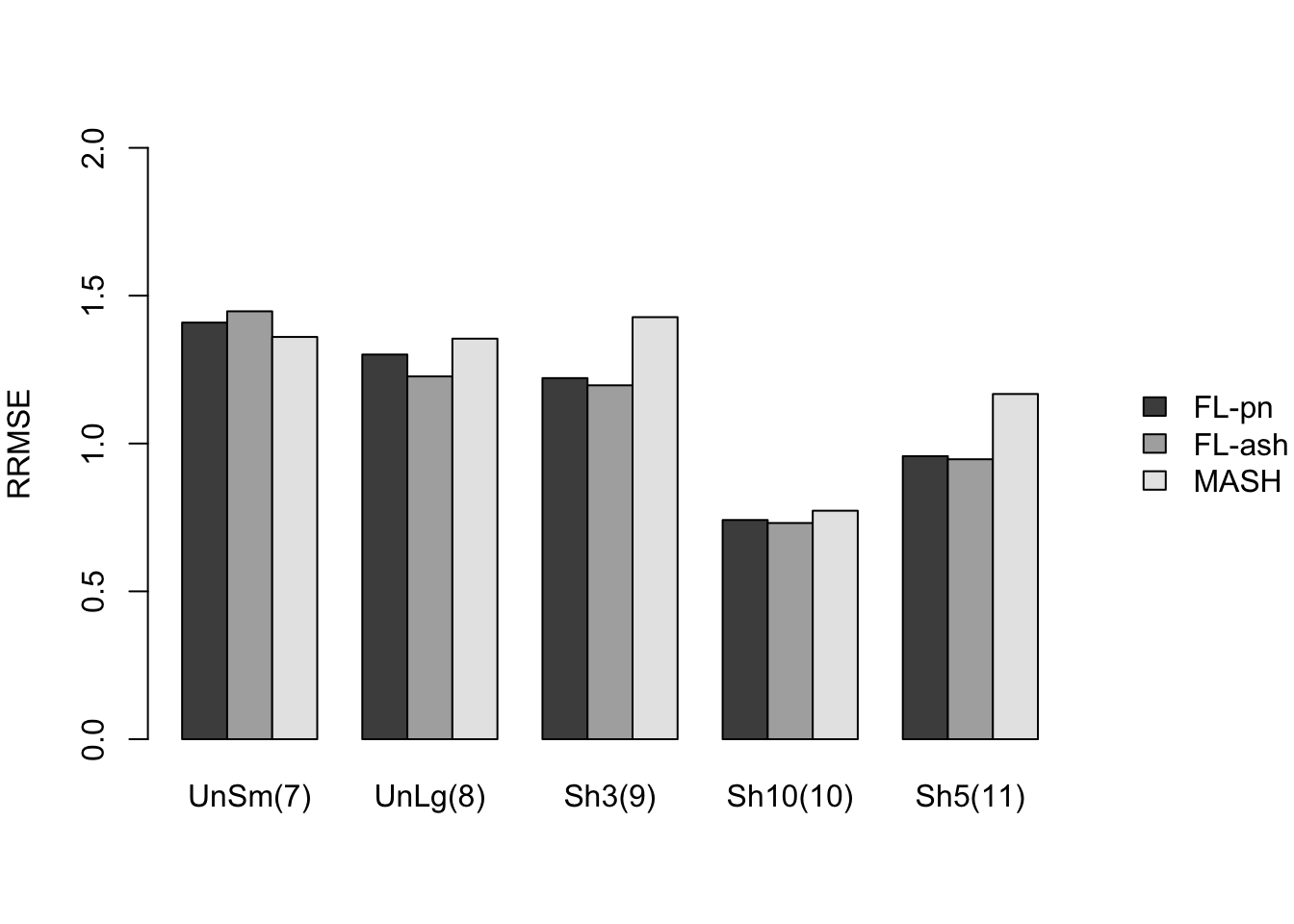
Expand here to see past versions of mse_nonnull-2.png:
| Version | Author | Date |
|---|---|---|
| 0a83e6c | Jason Willwerscheid | 2018-07-22 |
| ce6e790 | Jason Willwerscheid | 2018-06-26 |
| 17ae3f3 | Jason Willwerscheid | 2018-06-24 |
barplot(all.rrmses[,otheridx], names.arg = other.names, beside=T,
ylim=c(0, 2), ylab="RRMSE", main="",
legend.text=legend.names, args.legend=legend.args)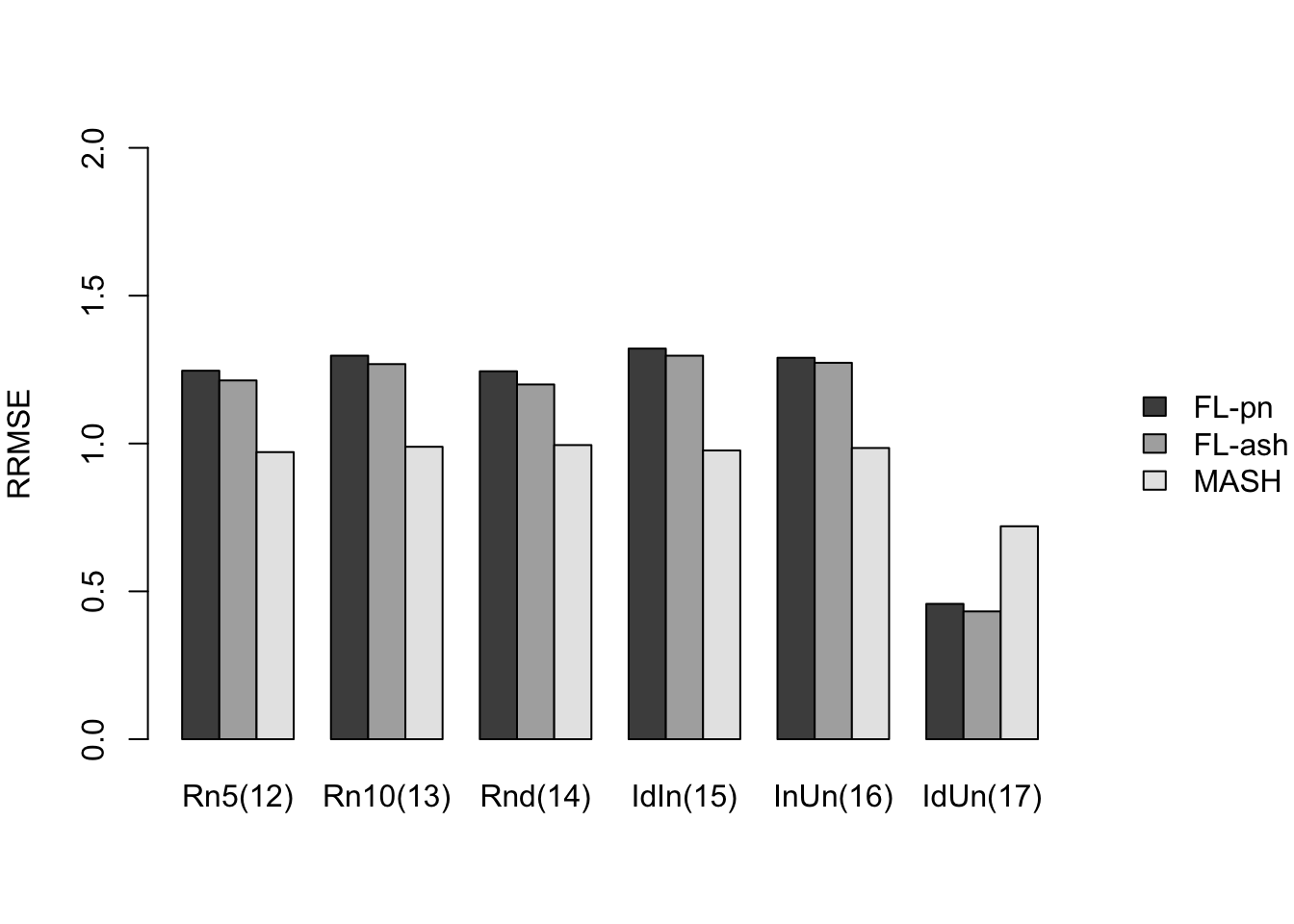
Results: FPR/TPR
As in the larger simulation study, I evaluate true and false positive rates using the built-in function get_lfsr() for MASH and by simulating from the posterior for FLASH. For each covariance structure, I plot the true positive rate for a given covariance structure against the overall false positive rate.
An examination of the ROC curves leads to somewhat different conclusions to the above. As above, MASH does much better with respect to independent effects (types 1-3), random covariance matrices (types 12-14), and a combination of identical and independent effects (type 15), while FLASH outperforms MASH on a combination of identical and unique effects (type 17). Interestingly, point-normal priors outperform ash priors in all of these cases.
MASH does slightly better with respect to both identical effects (types 4-5) and rank-one effects (type 6), even though FLASH did better on the latter in terms of RRMSE. All methods perform similarly for both unique and shared effects (types 7-11), with ash priors doing somewhat better than point-normal priors for unique effects. Both MASH and FLASH-pn do well on a combination of independent and unique effects, while FLASH-ash performs poorly.
In general, it appears that one can safely opt for the faster point-normal priors over the slower but more flexible ash priors.
get_fpr <- function(pr) {
nullidx <- c(7, 9, 11, 13, 15)
fp <- 25 * rowSums(pr[, nullidx]) + 775 * (pr[, 23])
fp / (25 * length(nullidx) + 775)
}
plot_fprvtpr <- function(idx, typename) {
plot(get_fpr(pr.pn), pr.pn[, idx], type='l', col="red1", lty=2,
xlab="FPR", ylab="TPR", ylim=c(0, 1), main=typename)
lines(get_fpr(pr.ash), pr.ash[, idx], col="red4", lty=2)
lines(get_fpr(pr.m), pr.m[, idx], col="blue")
legend("bottomright", legend=c("Fl-pn", "Fl-ash", "MASH"),
col=c("red1", "red4", "blue"), lty=c(2, 2, 1))
}
par(mfrow=c(1, 3))
plot_fprvtpr(1, "Small independent (1)")
plot_fprvtpr(2, "Large independent (2)")
plot_fprvtpr(3, "Independent of varying size (3)")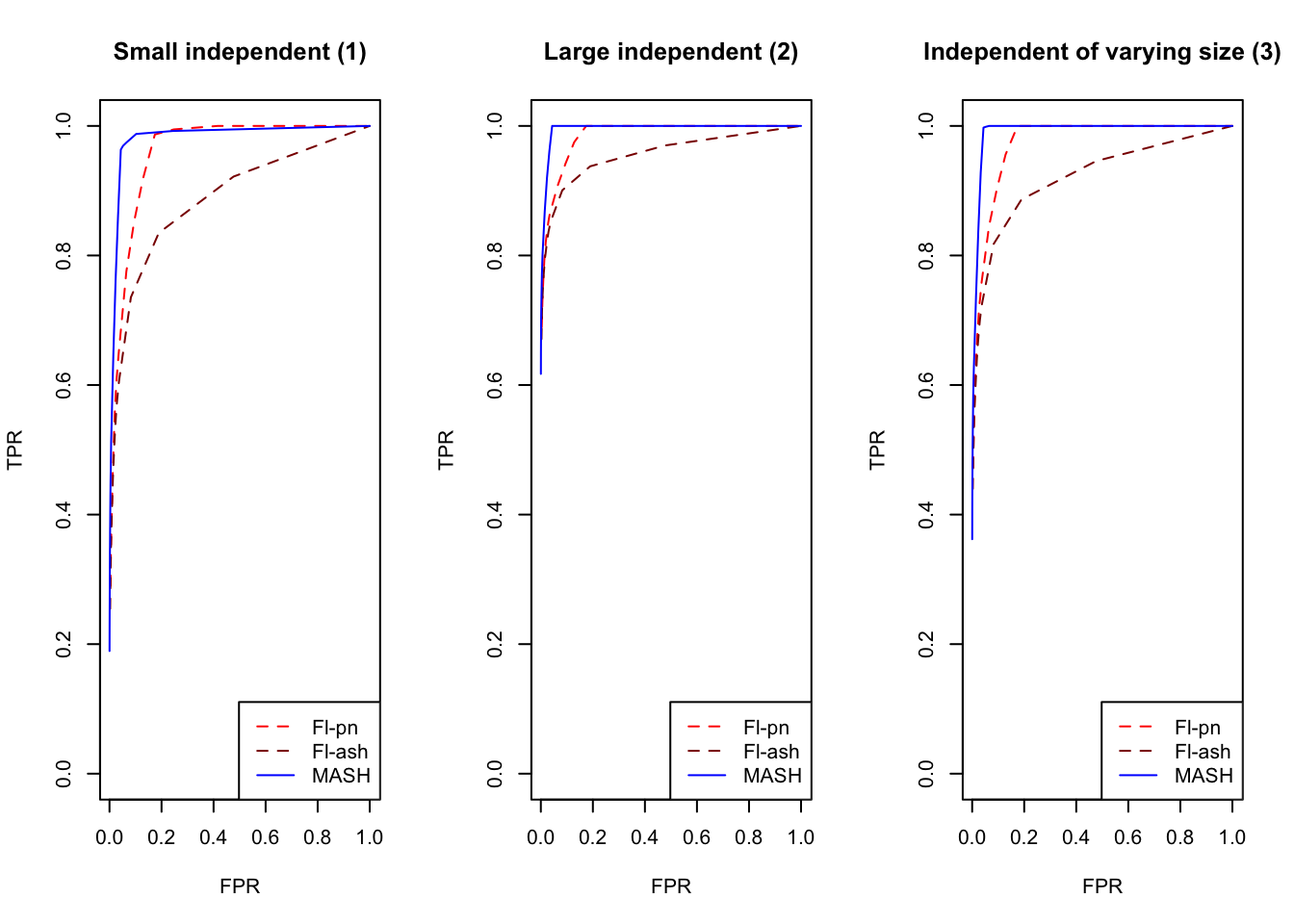
Expand here to see past versions of tpr-1.png:
| Version | Author | Date |
|---|---|---|
| 0a83e6c | Jason Willwerscheid | 2018-07-22 |
| ce6e790 | Jason Willwerscheid | 2018-06-26 |
| 17ae3f3 | Jason Willwerscheid | 2018-06-24 |
plot_fprvtpr(4, "Small identical (4)")
plot_fprvtpr(5, "Large identical (5)")
plot_fprvtpr(6, "Rank-one (6)")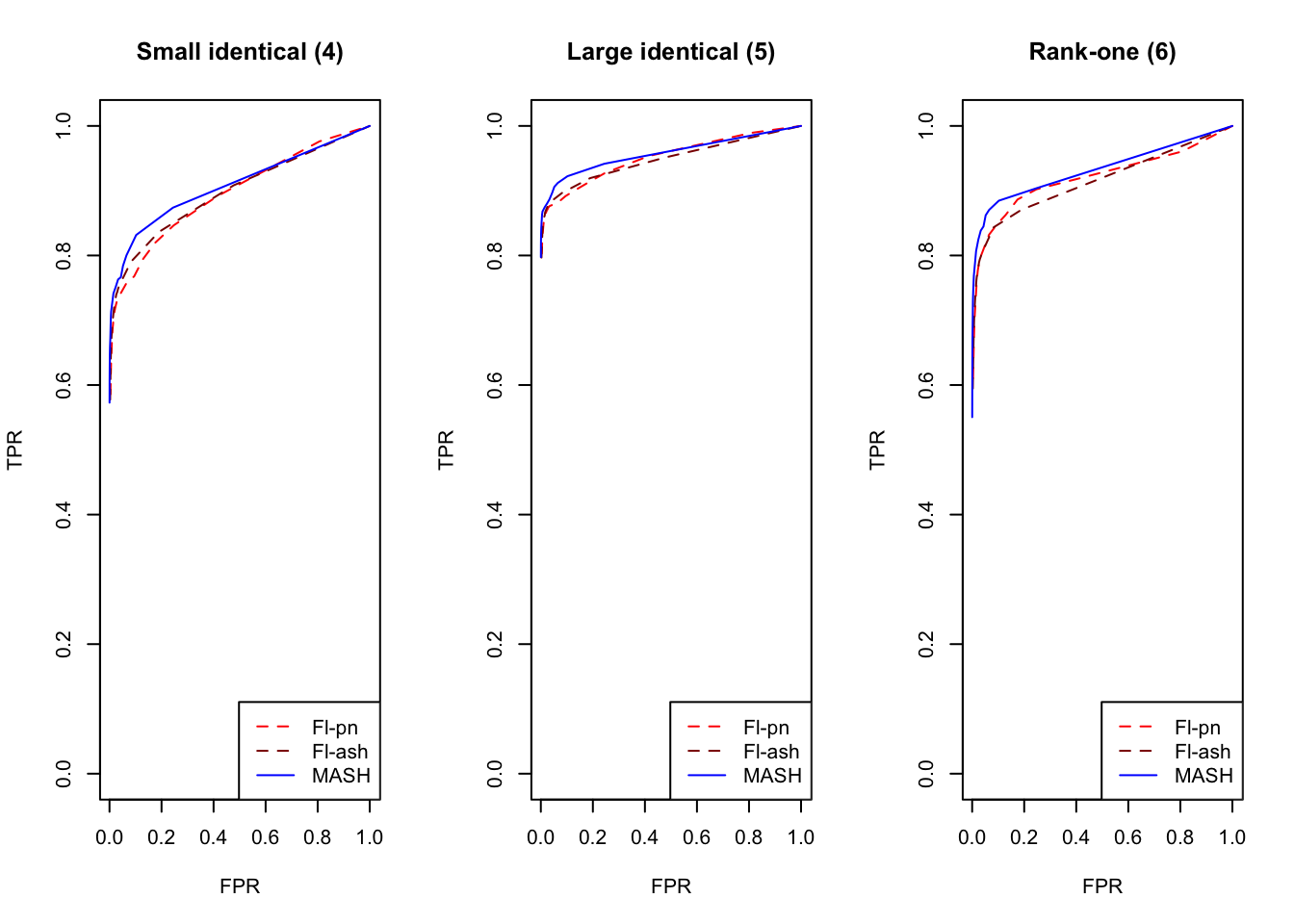
Expand here to see past versions of tpr-2.png:
| Version | Author | Date |
|---|---|---|
| 0a83e6c | Jason Willwerscheid | 2018-07-22 |
| ce6e790 | Jason Willwerscheid | 2018-06-26 |
| 17ae3f3 | Jason Willwerscheid | 2018-06-24 |
par(mfrow=c(1, 2))
plot_fprvtpr(8, "Small unique (7)")
plot_fprvtpr(10, "Large unique (8)")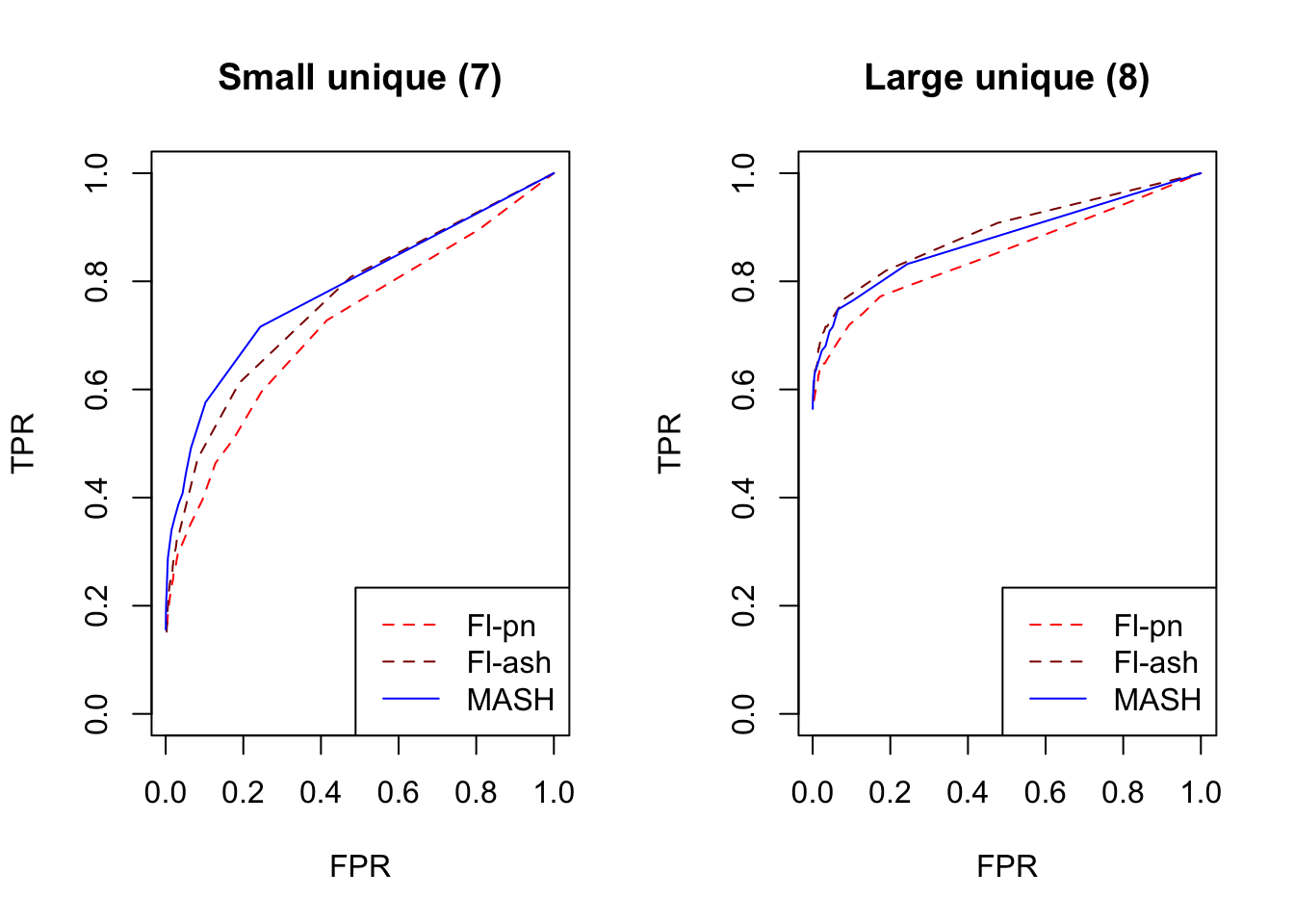
Expand here to see past versions of tpr-3.png:
| Version | Author | Date |
|---|---|---|
| 0a83e6c | Jason Willwerscheid | 2018-07-22 |
| ce6e790 | Jason Willwerscheid | 2018-06-26 |
| 17ae3f3 | Jason Willwerscheid | 2018-06-24 |
par(mfrow=c(1, 3))
plot_fprvtpr(12, "Shared (3 conditions) (9)")
plot_fprvtpr(14, "Shared (10 conditions) (10)")
plot_fprvtpr(16, "Shared (varying sizes) (11)")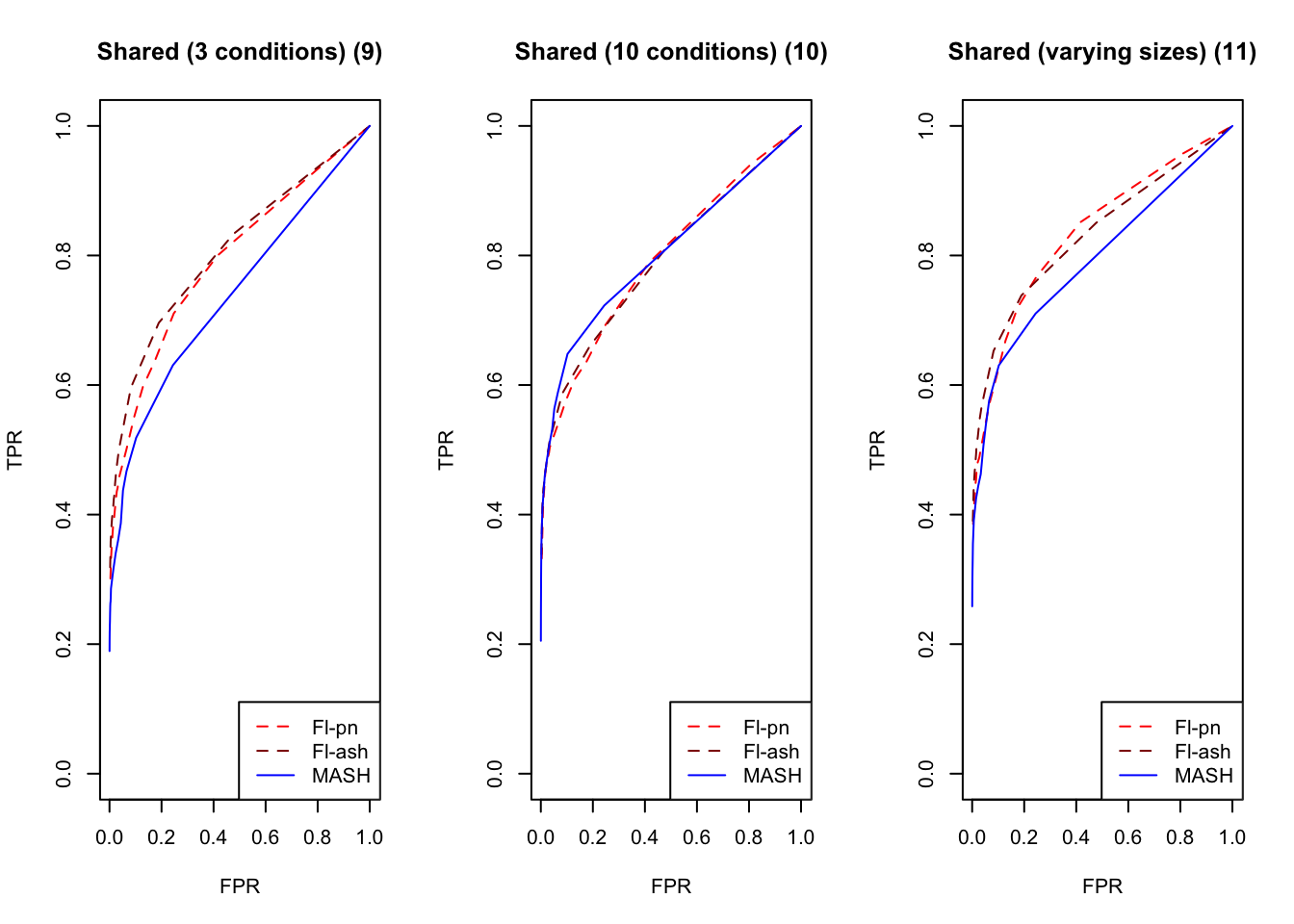
Expand here to see past versions of tpr-4.png:
| Version | Author | Date |
|---|---|---|
| 0a83e6c | Jason Willwerscheid | 2018-07-22 |
| ce6e790 | Jason Willwerscheid | 2018-06-26 |
plot_fprvtpr(17, "Random rank-5 (12)")
plot_fprvtpr(18, "Random rank-10 (13)")
plot_fprvtpr(19, "Random full-rank (14)")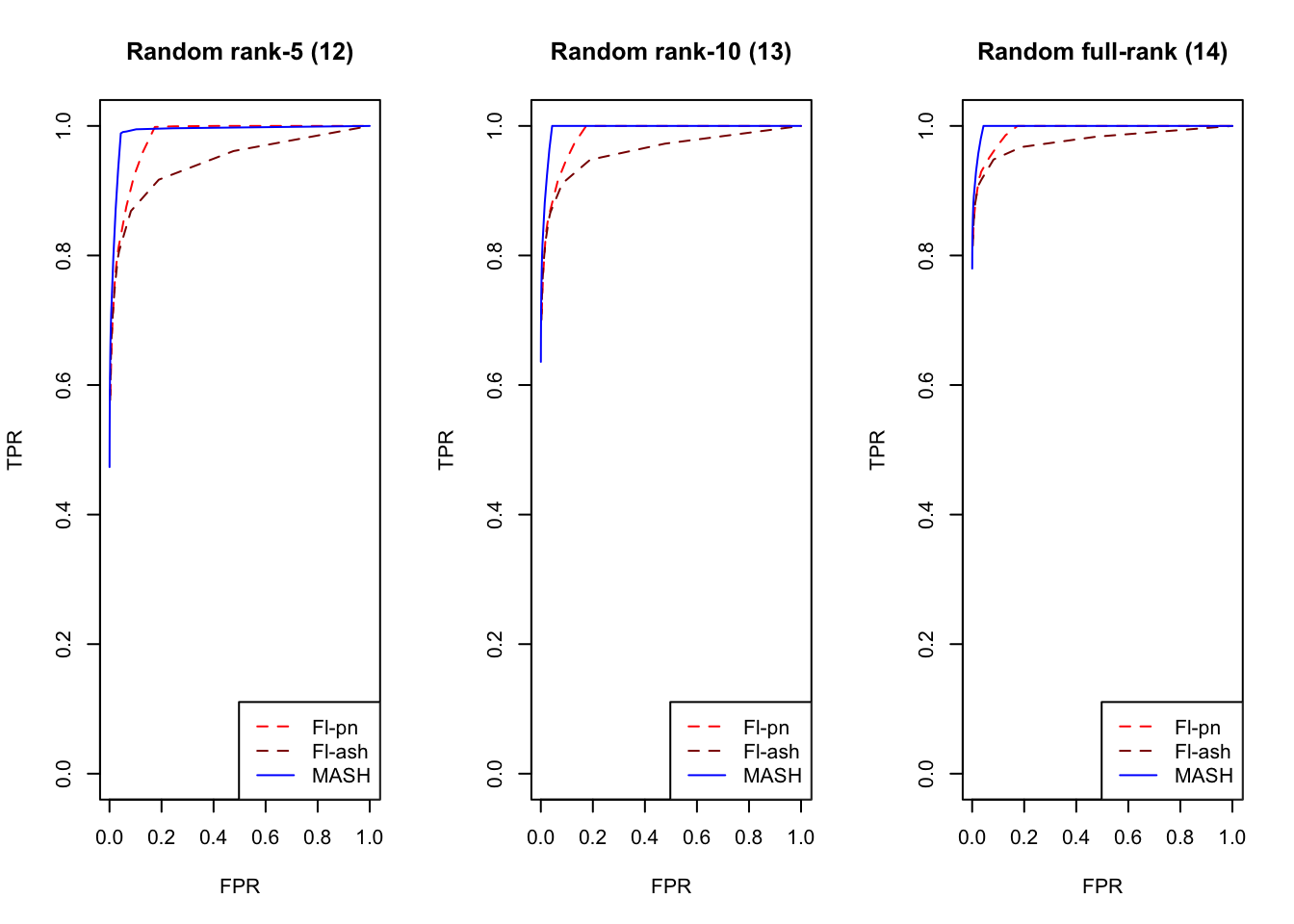
Expand here to see past versions of tpr-5.png:
| Version | Author | Date |
|---|---|---|
| 0a83e6c | Jason Willwerscheid | 2018-07-22 |
| ce6e790 | Jason Willwerscheid | 2018-06-26 |
plot_fprvtpr(20, "Identical plus independent (15)")
plot_fprvtpr(21, "Independent plus unique (16)")
plot_fprvtpr(22, "Identical plus unique (17)")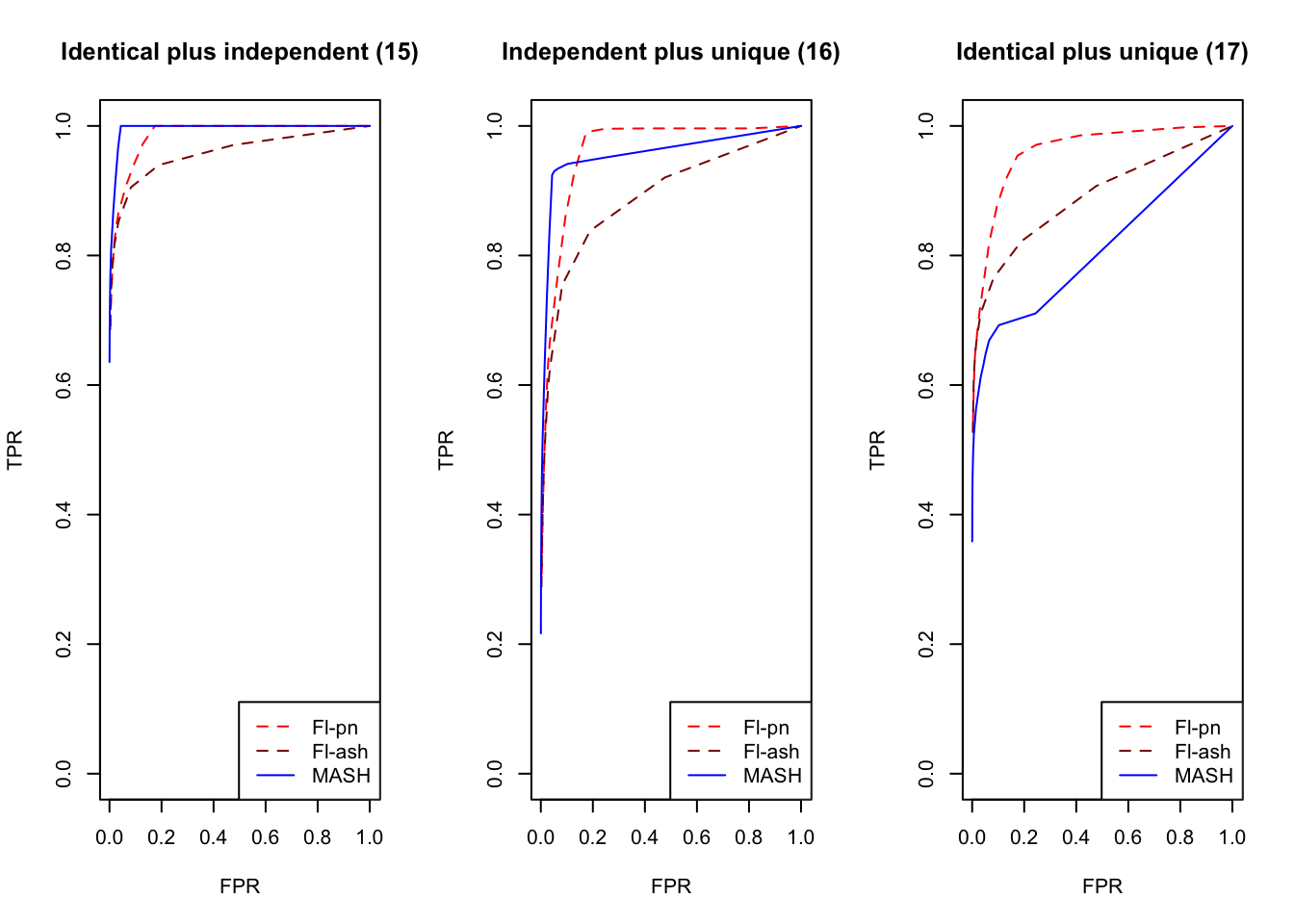
Code
Click “Code” to view the code used to obtain the above results.
devtools::load_all("/Users/willwerscheid/GitHub/flashr/")
library(mashr)
source("./code/fits.R")
source("./code/sims.R")
source("./code/utils.R")
set.seed(1)
n <- 20
p <- 1200
nsims <- 10
nsamp <- 200 # for sampling lfsr (FLASH fits)
ncol <- 25 # number of columns that exhibit each variance type
t <- 0.05 # "significance" threshold
Sigma <- list()
# Independent (small)
Sigma[[1]] <- diag(2^2, n)
# Independent (large)
Sigma[[2]] <- diag(5^2, n)
# Independent (different sizes)
sizes <- seq(1, 5, length.out=n)
Sigma[[3]] <- diag(sizes^2)
# Identical (small)
Sigma[[4]] <- matrix(2^2, nrow=n, ncol=n)
# Identical (large)
Sigma[[5]] <- matrix(5^2, nrow=n, ncol=n)
# Rank-one
Sigma[[6]] <- outer(sizes, sizes)
zeros <- matrix(0, nrow=n, ncol=n)
for (j in 7:11) {
Sigma[[j]] <- zeros
}
# Unique (small)
uniqsmidx <- 1
Sigma[[7]][uniqsmidx, uniqsmidx] <- 3^2
# Unique (large)
uniqlgidx <- 2
Sigma[[8]][uniqlgidx, uniqlgidx] <- 8^2
# Shared (3 conditions)
shar3idx <- 3:5
Sigma[[9]][shar3idx, shar3idx] <- matrix(3^2, nrow=3, ncol=3)
# Shared (10 conditions)
shar10idx <- 1:10
Sigma[[10]][shar10idx, shar10idx] <- matrix(2^2, nrow=10, ncol=10)
# Shared (5 conditions, different sizes)
shar5idx <- 6:10
sizes <- seq(2, 4, length.out=5)
Sigma[[11]][shar5idx, shar5idx] <- outer(sizes, sizes)
# Rank-5
A <- matrix(rnorm(n*5, 0, 2), nrow=5, ncol=n)
Sigma[[12]] <- t(A) %*% A
# Rank-10
A <- matrix(rnorm(n*10, 0, 2), nrow=10, ncol=n)
Sigma[[13]] <- t(A) %*% A
# Random
A <- matrix(rnorm(n*n, 0, 2), nrow=n, ncol=n)
Sigma[[14]] <- t(A) %*% A
# Large independent plus small identical
Sigma[[15]] <- Sigma[[2]] + Sigma[[4]]
# Small independent plus large unique
Sigma[[16]] <- Sigma[[1]] + Sigma[[8]]
# Small identical plus large unique
Sigma[[17]] <- Sigma[[4]] + Sigma[[8]]
ntypes <- 17
partnames <- c("IndSm", "IndLg", "IndDiff",
"IdentSm", "IdentLg", "Rank1",
"UniqSmNull", "UniqSmNonnull",
"UniqLgNull", "UniqLgNonnull",
"Shar3Null", "Shar3Nonnull",
"Shar10Null", "Shar10Nonnull",
"Shar5Null", "Shar5Nonnull",
"Rank5", "Rank10", "Random",
"IndIdent", "IndUniq", "IdentUniq",
"Null")
partxidx <- list(1:n, 1:n, 1:n, 1:n, 1:n, 1:n,
setdiff(1:n, uniqsmidx), uniqsmidx,
setdiff(1:n, uniqlgidx), uniqlgidx,
setdiff(1:n, shar3idx), shar3idx,
setdiff(1:n, shar10idx), shar10idx,
setdiff(1:n, shar5idx), shar5idx,
1:n, 1:n, 1:n, 1:n, 1:n, 1:n, 1:n)
partyidx <- list(1:ncol, ncol + 1:ncol, 2*ncol + 1:ncol,
3*ncol + 1:ncol, 4*ncol + 1:ncol, 5*ncol + 1:ncol,
6*ncol + 1:ncol, 6*ncol + 1:ncol,
7*ncol + 1:ncol, 7*ncol + 1:ncol,
8*ncol + 1:ncol, 8*ncol + 1:ncol,
9*ncol + 1:ncol, 9*ncol + 1:ncol,
10*ncol + 1:ncol, 10*ncol + 1:ncol,
11*ncol + 1:ncol, 12*ncol + 1:ncol,
13*ncol + 1:ncol, 14*ncol + 1:ncol,
15*ncol + 1:ncol, 16*ncol + 1:ncol,
(17*ncol + 1):p)
nparts <- length(partnames)
partition_by_type <- function(X) {
ret <- rep(0, nparts)
for (i in 1:nparts) {
ret[i] <- mean(X[partxidx[[i]], partyidx[[i]]])
}
names(ret) <- partnames
ret
}
mses <- matrix(0, nrow=3, ncol=nparts)
ts <- c(seq(.005, .05, by=.005), seq(.06, .1, by=.01), seq(.2, 1.0, by=.1))
pr.pn <- matrix(0, nrow=length(ts), ncol=nparts)
pr.ash <- matrix(0, nrow=length(ts), ncol=nparts)
pr.m <- matrix(0, nrow=length(ts), ncol=nparts)
for (i in 1:nsims) {
X <- matrix(0, nrow=n, ncol=p)
for (j in 1:ntypes) {
start_col = 1 + ncol*(j-1)
end_col = ncol*j
X[, start_col:end_col] <- t(MASS::mvrnorm(ncol, rep(0, n), Sigma[[j]]))
}
Y <- X + rnorm(n*p)
fl.pn <- fit_flash(Y, Kmax=30, methods=3, ebnm_fn="ebnm_pn") # OHL
fl.ash <- fit_flash(Y, Kmax=30, methods=3, ebnm_fn="ebnm_ash")
m <- fit_mash(Y)
base.se <- (Y - X)^2
base.mse <- partition_by_type(base.se)
fl.pn.se <- (flash_get_fitted_values(fl.pn$fits$OHL) - X)^2
fl.pn.mse <- partition_by_type(fl.pn.se) / base.mse
fl.ash.se <- (flash_get_fitted_values(fl.ash$fits$OHL) - X)^2
fl.ash.mse <- partition_by_type(fl.ash.se) / base.mse
m.se <- (t(get_pm(m$m)) - X)^2
m.mse <- partition_by_type(m.se) / base.mse
mses[1,] <- mses[1,] + fl.pn.mse
mses[2,] <- mses[2,] + fl.ash.mse
mses[3,] <- mses[3,] + m.mse
fl.pn.sampler <- flash_sampler(Y, fl.pn$fits$OHL, fixed="loadings")
fl.pn.samp <- fl.pn.sampler(nsamp)
fl.pn.lfsr <- flash_lfsr(fl.pn.samp)
fl.ash.sampler <- flash_sampler(Y, fl.ash$fits$OHL, fixed="loadings")
fl.ash.samp <- fl.ash.sampler(nsamp)
fl.ash.lfsr <- flash_lfsr(fl.ash.samp)
m.lfsr <- t(get_lfsr(m$m))
for (j in 1:length(ts)) {
fl.pn.signif <- fl.pn.lfsr <= ts[j]
fl.pn.pr <- partition_by_type(fl.pn.signif)
fl.ash.signif <- fl.ash.lfsr <= ts[j]
fl.ash.pr <- partition_by_type(fl.ash.signif)
m.signif <- m.lfsr <= ts[j]
m.pr <- partition_by_type(m.signif)
pr.pn[j,] <- pr.pn[j,] + fl.pn.pr
pr.ash[j,] <- pr.ash[j,] + fl.ash.pr
pr.m[j,] <- pr.m[j,] + m.pr
}
}
mses <- mses / nsims
pr.pn <- pr.pn / nsims
pr.ash <- pr.ash / nsims
pr.m <- pr.m / nsims
saveRDS(mses, "./output/sims2mse.rds")
saveRDS(pr.pn, "./output/sims2prpn.rds")
saveRDS(pr.ash, "./output/sims2prash.rds")
saveRDS(pr.m, "./output/sims2prm.rds")Session information
sessionInfo()R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.1
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
loaded via a namespace (and not attached):
[1] workflowr_1.0.1 Rcpp_0.12.17 digest_0.6.15
[4] rprojroot_1.3-2 R.methodsS3_1.7.1 backports_1.1.2
[7] git2r_0.21.0 magrittr_1.5 evaluate_0.10.1
[10] stringi_1.1.6 whisker_0.3-2 R.oo_1.21.0
[13] R.utils_2.6.0 rmarkdown_1.8 tools_3.4.3
[16] stringr_1.3.0 yaml_2.1.17 compiler_3.4.3
[19] htmltools_0.3.6 knitr_1.20 This reproducible R Markdown analysis was created with workflowr 1.0.1