6. Как классифицировать текст
Обнаружение моделей является центральной частью обработки естественного языка. Слова, оканчивающиеся на -ed, как правило, глаголы прошедшего времени (5.). Частое использование will свидетельствует о новостном тексте (3). Эти наблюдаемые паттерны - структура слова и частота слово - случается коррелируют с конкретными аспектами смысла, такими как время и тема. Но как мы узнали, где начать искать, какие аспекты формы связать с какими аспектами смысла?
Цель этой главы - ответить на следующие вопросы:
- Как мы можем идентифицировать специфические особенности языковых данных, которые являются характерными для их классификации?
- Как мы можем строить модели языка, которые могут быть использованы для автоматического выполнения задач по обработке языка?
- Что мы можем узнать о языке из этих моделей?
Параллельно мы рассмотрим некоторые важные методы машинного обучения, в том числе деревья решений, наивные классификаторы Байеса, и классификаторы максимальной энтропии. Мы будем не будем разбирать математические и статистические основы этих методов, а сосредоточимся на том, как и когда использовать их (см. раздел Дополнительные материалы для получения дополнительной технической информации). Прежде чем рассматривать эти методы, мы в первую очередь должны оценить масштаб этой темы.
1 Контролируемая классификация
Классификация является задачей выбора правильной метки класса для данного входа. В основных задачах классификации каждый вход рассматривается в отрыве от всех остальных входов, а множество меток определяется заранее. Некоторые примеры задач классификации:
- Принятие решения, является ли письмо спамом или нет.
- Выбор темы новостной статьи из фиксированного списка тематических областей, таких как "спорт", "технологии" и "политика".
- Выбор референта для данного вхождение слова bank из возможных: берег реки, финансовое учреждение, акт наклона в сторону или акт размещения чего-либо в финансовом учреждении.
Основная задача классификации имеет ряд интересных вариантов. Например, в мультиклассификации каждому экземпляру может быть назначено множество меток; в классификации с открытыми классами набор меток не определен заранее; а в классификации последовательности список входов классифицируется совместно.
Классификатор называется контролируемым, если он построен на основе тренировочного корпуса, содержащего правильную метку для каждого входа. Схема контролируемой классификации показана на 1.1.
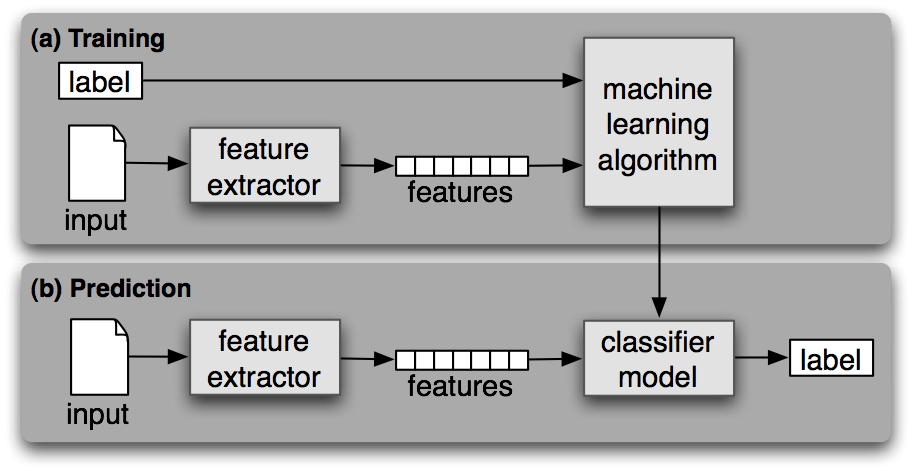
Рисунок 1.1: Контролируемая классификация. (a) Во время тренировки, экстрактор свойств используется для преобразования каждого значения входного сигнала в набор свойств. Эти наборы свойств, которые схватывают основную информацию о каждом входе, которая должны быть использована для его классификации, обсуждаются в следующем разделе. Пары наборов свойств и меток подаются в алгоритм машинного обучения, чтобы создать модель. (b) Во время предсказания, тот же экстрактор свойств используется для преобразования невидимых входов в наборы свойств. Эти наборы свойств затем подаются в модель, которая генерирует предсказанные метки.
В оставшейся части этого раздела мы рассмотрим, как классификаторы могут быть использованы для решения широкого спектра задач. Наше обсуждение не претендует на полноту, но стремится дать показательную выборку задач, которые могут быть выполнены с помощью текстовых классификаторов.
1.1 Половая идентификация
В 4 мы увидели, что мужские и женские имена имеют некоторые отличительные особенности. Имена, оканчивающиеся на a, e и i, вероятно, будут женскими, в то время как имена, заканчивающиеся на k, o, r, s и t, вероятно, будут мужскими. Давайте построим классификатор, чтобы смоделировать эти различия более точно.
Первым шагом в создании классификатор является решение о том, какие свойства входа релевантны и как кодировать эти свойства. Для этого примера мы начнем с заключительной буквы имени. Следующая функция извлечения свойств создает словарь, содержащий соответствующую информацию о данном имени:
|
Возвращенный словарь, известный как набор свойств ставит в соответствие имена свойств и их значения. Названия свойств - это чувствительные к регистру строки, которые обычно предоставляют короткое легко читаемое описание свойства, как в нашем примере 'last_letter'. Значения свойств - это значения с простыми типами, такими как логические значения, числа и строки.
Замечание
Большинство методов классификации требуют, чтобы свойства были закодированы с помощью простых типов значений, таких как логические значения, числа и строки. Но обратите внимание: только то, что свойство имеет простой тип, не обязательно означает, что значение свойства просто выразить или вычислить. На самом деле, в качестве свойств можно даже использовать очень сложные и содержательные значения, такие как выход второго контролируемого классификатора.
Теперь, когда мы определили экстрактор свойств, нам необходимо подготовить перечень примеров и соответствующие метки классов.
|
Далее мы используем экстрактор свойств для обработки данных names и разделить полученный список наборов свойств на тренировочный набор и тестовый набор. Тренировочный набор используется для подготовки нового «наивного классификатора Байеса".
|
Мы узнаем больше о наимвном классификаторе Байеса позже в этой главе. На данный момент давайте просто проверим его на несколько именах, которых не было в обучающих данных:
|
Заметим, что эти имена персонажей из Матрицы классифицированы правильно. Хотя этот научно-фантастический фильм рассказывает о событиях 2199 года, он все же соответствует нашим ожиданиям об именах и полах. Мы можем систематически оценивать классификатор на гораздо большем количестве невидимых данных:
|
И, наконец, мы можем исследовать классификатор, чтобы определить, какие из свойств, которые он нашел, наиболее эффективны для различения имен по гендерному признаку:
|
Этот список показывает, что имена в обучающем наборе, которые заканчиваются на "a" являются женскими в 33 раза чаще, чем мужскими, а имена, которые заканчиваются на "k" являются мужскими в 32 раза чаще, чем женскими. Эти соотношения известны как доли вероятности и могут быть полезны для сравнения различных отношений свойство-результат.
Замечание
Ваша очередь: Измените функцию gender_features(), чтобы предоставить классификатору свойства, кодирующие длину имени, его первую букву, а также любые другие свойства, которые вам покажутся информативными. Повторите тренировку классификатора с этими новыми свойствами и проверьте его точность.
При работе с большими корпусами построения единого списка, который содержит в себе свойства всех экземпляров может занимать большой объем памяти. В этих случаях используйте функцию nltk.classify.apply_features, которая возвращает объект, который действует как список, но не хранит все наборы свойств в памяти:
|
1.2 Выбор правильных свойств
Выбор релевантных свойств и принятие решения, как кодировать их для метода обучения, может иметь огромное влияние на способность метода обучения извлекать хорошую модель. Большая часть интересной работы при построении классификатора - это выбор свойств, которые могут быть релевантными, и решение вопроса о том, как мы можем их представить. Несмотря на то, что часто можно получить приличную производительность, используя довольно простой и очевидный набор свойств, обычно есть значительные выгоды от использования тщательно выстроенных свойств на основе глубокого понимания задачи.
Как правило, экстракторы свойств строятся методом проб и ошибок под руководством интуиций о том, какая информация имеет отношение к этой проблеме. Общераспространенным является начало с подхода "кухонная раковина", когда в дело идут все свойства, которые вы можете придумать, а затем выполняется проверка того, какие свойства, на самом деле, являются полезными. Мы принимаем этот подход гендерных свойств имени в 1.2.
| ||
| ||
Пример 1.2 (code_gender_features_overfitting.py): Листинг 1.2: Экстрактор свойств, который не соответствует гендерным свойствам. Набор свойств, возвращаемый этим экстрактором свойств содержат большое количество специфических свойств, ведущих к "переобученности" для относительно небольшого корпуса имен. |
Однако обычно есть ограничения на количество свойств, которые вы должны использовать с заданным алгоритмом обучения - если вы предоставляете слишком много свойств, то алгоритм будет иметь более высокий шанс полагаться на стилистические особенности ваших тренировочных данных, которые плохо обобщают новые примеры. Эта проблема известна как переобученность и может быть особенно проблематичной при работе с небольшими наборами тренировочных данных. Например, если мы тренируем наивный байесовский классификатор, используя экстрактор свойств, показанный в 1.2, он будет переобучен относительно небольшого тренировочного набора, в результате чего будет создана модель, в которой точность составляет около 1% ниже, чем точность классификатора, который только обращает внимание на последнюю букву каждого имени:
|
После того, как первоначальный набор свойств был выбран, очень продуктивным методом для уточнения набора свойств является анализ ошибок. Сначала мы выбираем набор для разработки, содержащий данные для создания модели. Этот набор разработки затем делится на тренировочный набор и тестовый (dev-test) набор.
|
Тренировочный набор разработки используется для обучения модели, а тестовый набор разработки (dev-test) используется для выполнения анализа ошибок. Тестовый (test) набор используется в нашей окончательной оценке системы. По причинам, изложенным ниже, важно, чтобы мы использовали отдельный набор для анализа ошибок (dev-test ), а не просто тестовый набор (test set). Разделение данных корпуса на различные наборы показано в 1.3.
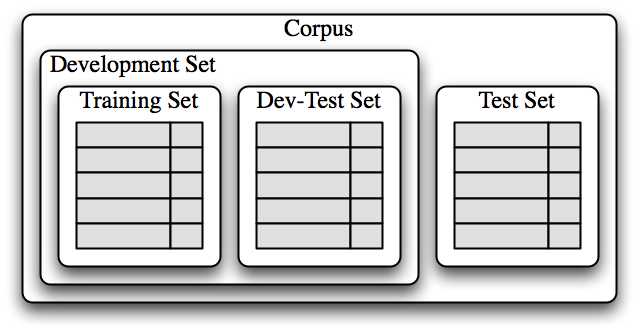
Рисунок 1.3: Организация данных корпуса для обучения контролируемых классификаторов. Данные корпуса делятся на две группы: набор разработки и тестовый набор. Набор разработки часто подразделяется на тренировочный набор и тестовый набор разработки.
Разделив корпус на соответствующие наборы данных, мы готовим модель, используя тренировочный набор ![[1]](http://www.nltk.org/book/callouts/callout1.gif) , а затем прогоняем ее на тестовом наборе разработки
, а затем прогоняем ее на тестовом наборе разработки![[2]](http://www.nltk.org/book/callouts/callout2.gif) .
.
|
Используя тестовый набор разработки, мы можем сгенерировать список ошибок, которые классификатор делает при прогнозировании пола имени:
|
Затем мы можем исследовать отдельные случаи ошибок, когда модель предсказала неправильную метку, и попытаться определить, какие дополнительные элементы информации позволили бы ей принять правильное решение (или какие существующие фрагменты информации заставляют ее принять неправильное решение). Набор свойств может быть соответствующим образом скорректирован. Классификатор имен, который мы построили, генерирует около 100 ошибок на на тестовом наборе разработки:
|
Просматривая этот список ошибок становится ясно, что некоторые суффиксы, состоящие из двух и более букв, могут указывать на мужское или женское имя. Например, имена, заканчивающиеся на yn оказываются преимущественно женскими, несмотря на то, что имена, оканчивающиеся на n имеют тенденцию быть мужскими; а имена, заканчивающиеся на ch обычно мужские, несмотря на то, что имена, которые заканчиваются на h, как правило, женские. Поэтому мы скорректируем наш экстрактор свойств и включим в него свойства для двухбуквенных суффиксов:
|
Перестроив классификатор с новым экстрактором свойств, мы видим, что результативность на тестовом наборе разработки улучшается почти на 2 процентных пункта (с 76,5% до 78,2%):
|
Эта процедура анализа ошибок может быть затем повторена для проверки паттернов ошибок, которые были сделаны недавно улучшенным классификатором. Каждый раз, когда повторяется процедура анализа ошибок, мы должны по-другому поделить данные на тренировочный и тестовый набор разработки, чтобы гарантировать, что классификатор не начинает отражать особенности тестового набора разработки.
Но как только мы использовали тестовый набор разработки для подготовки модели, мы больше не можем верить, что он даст нам точное представление о том, как хорошо модель будет работать на новых данных. Поэтому важно держать тестовый набор отдельно и не использовать его, пока наша разработка модели не будет завершена. Когда разработка будет завершена, мы можем использовать тестовый набор, чтобы оценить, насколько хорошо наша модель будет работать на новых входных данных.
1.3 Классификация документов
В 1 мы видели несколько примеров корпусов, в которых документы были помечены категориями. Используя эти корпусы, мы можем построить классификаторы, которые будут автоматически помечать новые документы соответствующими метками категорий. Сначала мы строим перечень документов, помеченных соответствующими категориями. Для этого примера мы выбрали корпус отзывов на фильмы, который классифицирует каждый обзор как положительный или отрицательный.
|
Далее мы определяем экстрактор свойств для документов, чтобы классификатор знал, на какие аспекты данных следует обратить внимание (1.4). Для идентификации темы документа, мы можем определить свойство для каждого слова, указывающее, содержит ли документ это слово. Чтобы ограничить количество свойств, которые классификатор должен обрабатывать, мы начинаем с построения списка 2000 наиболее частых слов в общем корпусе ![[1]](http://www.nltk.org/book/callouts/callout1.gif) . Затем мы можем определить экстрактор свойств
. Затем мы можем определить экстрактор свойств ![[2]](http://www.nltk.org/book/callouts/callout2.gif) , который просто проверяет, присутствует ли каждое из этих слов в данном документе.
, который просто проверяет, присутствует ли каждое из этих слов в данном документе.
| ||
| ||
Пример 1.4 (code_document_classify_fd.py) : Листинг 1.4: Экстрактор свойств для классификации документов, чьи свойства указывают, присутствуют ли отдельные слова в данном документе. |
Замечание
Причина, по которой мы вычисляем набор всех слов в документе в ![[3]](http://www.nltk.org/book/callouts/callout3.gif) иная, нежели просто проверка, присутствует ли слово в документе, дело в том, что проверка наличия слова в наборе гораздо быстрее, чем проверка наличия его в списке (4.7).
иная, нежели просто проверка, присутствует ли слово в документе, дело в том, что проверка наличия слова в наборе гораздо быстрее, чем проверка наличия его в списке (4.7).
Теперь, когда мы определили наш экстрактор свойств, мы можем использовать его, чтобы обучить классификатор помечать новые обзоры фильмов (1.5). Чтобы проверить, насколько надежен полученный классификатор, мы вычислим его точность на тестовом наборе ![[1]](http://www.nltk.org/book/callouts/callout1.gif) . И снова мы можем использовать show_most_informative_features(), чтобы выяснить, какие из найденных классификатором свойств оказались наиболее информативными
. И снова мы можем использовать show_most_informative_features(), чтобы выяснить, какие из найденных классификатором свойств оказались наиболее информативными ![[2]](http://www.nltk.org/book/callouts/callout2.gif) .
.
| ||
| ||
Пример 1.5 (code_document_classify_use.py): Листинг 1.5: Обучение и тестирование классификатора для классификации документов. |
По-видимому в этом корпусе отзыв, в котором упоминается "Сигал", имеет почти в 8 раз больше шансов быть отрицательным, чем положительным, в то время как отзыв, который упоминает "Дэймона", примерно в 6 раз более вероятно, что будет положительным.
Разметка частей речи
В 5. мы построили разметчик, использующий регулярное выражение, который выбирает метку части речи для слова, глядя на внутреннюю структуру слова. Однако мы должны были сконструировать этот разметчик вручную. Вместо этого мы можем обучить классификатор определять, какие суффиксы являются наиболее информативными. Давайте начнем с выяснения того, какие суффиксы наиболее распространенные:
|
|
Далее мы определим функцию извлечения свойств, которая проверяет данное слово на эти суффиксы:
|
Функции извлечения свойств ведут себя как тонированные стекла, выделяя некоторые из свойств (цветов) в наших данных и делая невозможным увидеть другие свойства. Классификатор будет опираться исключительно на эти подчеркнутые свойства при определении того, как пометить входы. В этом случае классификатор будет принимать свои решения только на основе информации о том, какие из общих суффиксов (если таковые имеются) имеет данное слово.
Теперь, когда мы определили нашу функцию-экстрактор, мы можем использовать ее для подготовки нового классификатора на основе "дерева решений" (будет обсуждаться в 4):
|
|
|
|
Одна хорошая особенность моделей на основе дерева решений состоит в том, что их часто довольно легко интерпретировать - мы можем даже поручить NLTK печатать их как псевдокод:
|
Здесь мы видим, что классификатор начинает с проверки, заканчивается ли слово запятой - если это так, то оно получит специальную метку ",". Далее классификатор проверяет, заканчивается ли слово на "the", в этом случае оно почти наверняка определитель. Этот "суффикс" используется в дереве решений, потому что слово "the" такое распространенное. Продолжая, классификатор проверяет, оканчивается ли слово на "s". Если это так, то , скорее всего, оно получит метку глагола VBZ (если это не слово "is", которое имеет специальную метку BEZ), а если нет, то это, скорее всего, существительное (если только это не знак препинания "."). Реальный классификатор содержит дальнейшие вложенные если-то предложения ниже тех, которые показаны здесь, но аргумент depth=4просто отображает верхнюю часть дерева решений.
1.5 Использование контекста
Путем добавления функции извлечения свойств мы могли бы изменить этот разметчик, чтобы он мог использовать множество других внутренних свойств слова, таких как длина слова, число слогов или его префикс. Однако до тех пор, пока экстрактор свойств просто смотрит на целевое слово, у нас нет никакого способа добавлять новые свойства, которые зависят от контекста, в котором слово появляется. Но контекстные возможности часто предоставляют мощные подсказки о правильной метке - например, при обработке слова "fly" знание о том, что предыдущее слово "a", позволит нам определить, что оно функционирует как существительное, а не глагол.
Для того чтобы учесть свойства, которые зависят от контекста данного слова, мы должны пересмотреть шаблон, который мы использовали для определения нашего экстрактор свойств. Вместо того, чтобы просто передавать слово, мы будем передавать полное (не помеченное) предложение с индексом целевого слова. Такой подход демонстрируется в 1.6, который использует экстрактор контекстно-зависимых свойств, чтобы определить классификатор частей речи.
| ||
| ||
Пример 1.6 (code_suffix_pos_tag.py): Листинг 1.6: Классификатор частей речи, чей детектор свойств анализирует контекст, в котором слово появляется для того, чтобы определить, какая метка части речи должна быть назначена. В частности, индивидуальность предыдущего слова включена в качестве свойства. |
Понятно, что использование контекстных свойств повышает результативность нашего разметчика частей речи. Например, классификатор узнает о том, что слово скорее всего является существительным, если оно идет сразу после слова "большой" или слова "губернаторского". Однако он не в состоянии выучить обобщение, что слово, вероятно, существительное, если оно следует за прилагательным, потому что он не имеет доступа к метке части речи предыдущего слова. В целом простые классификаторы всегда рассматривают каждый вход как независимый от всех других входов. Во многих случаях это имеет смысл. Например, решения о том, имеют ли имена тенденцию быть мужскими или женскими, могут быть приняты на основе перебора случаев. Однако часто бывают случаи, такие как разметка частей речи, где мы заинтересованы в решении проблем классификации, тесно связанных друг с другом.
1.6 Классификация последовательности
Для того, чтобы схватить зависимости между связанными задачами классификации, мы можем использовать модели объединенного классификатора, которые выбирают соответствующую маркировку для набора связанных входов. В случае разметки частей речи разнообразие различных моделей классификатора последовательности может быть использовано, для совместного выбора меток части речи для всех слов в данном предложении.
Одна из стратегий классификации последовательности, известная как последовательная классификация или жадные классификация последовательности, заключается в том, чтобы найти наиболее вероятную метку класса для первого входа, затем использовать этот ответ, чтобы найти лучшую метку для следующего входа. Затем процесс может повторяться до тех пор, пока все входные данные не были помечены. Это подход, который был принят биграмм-разметчиком из 5, который начал с выбора метки части речи для первого слова в предложении, а затем определял метку для каждого последующего слова на основе самого этого слова и предсказанной метки для предыдущего слова.
Эта стратегия показана в 1.7.
Сначала мы должны усилить нашу функцию извлечения свойств, чтобы она принимала аргумент history, который предоставляет список меток, которые мы уже предсказали для данного предложения![[1]](http://www.nltk.org/book/callouts/callout1.gif) .
Каждая метка в истории соответствует слову в предложении. Но учтите, что history будет содержать только метки для слов, которые мы уже классифицировали, то есть расположенных слева от целевого слова. Таким образом, в то время как можно посмотреть на некоторые особенности слов справа от целевого слова, не представляется возможным посмотреть на метки для этих слов (так как мы их еще не породили).
.
Каждая метка в истории соответствует слову в предложении. Но учтите, что history будет содержать только метки для слов, которые мы уже классифицировали, то есть расположенных слева от целевого слова. Таким образом, в то время как можно посмотреть на некоторые особенности слов справа от целевого слова, не представляется возможным посмотреть на метки для этих слов (так как мы их еще не породили).
Определив экстрактор свойств, мы можем приступить к созданию нашего классификатора последовательности ![[2]](http://www.nltk.org/book/callouts/callout2.gif) . Во время обучения мы используем аннотированные метки, чтобы предоставить экстрактору свойств соответствующую историю, но когда выполняется разметка новых предложений, мы формируем список истории на основе вывода самого разметчика.
. Во время обучения мы используем аннотированные метки, чтобы предоставить экстрактору свойств соответствующую историю, но когда выполняется разметка новых предложений, мы формируем список истории на основе вывода самого разметчика.
| ||
| ||
Пример 1.7 (code_consecutive_pos_tagger.py) : Листинг 1.7: Разметка частей речи с помощью классификатора последовательности |
1.7 Другие методы классификации последовательности
Один из недостатков этого подхода заключается в том, что мы придерживаемся каждого решения, которое мы приняли. Например, если мы решим пометить слово как существительное, но позже найдем доказательство того, что оно должно было быть глаголом, нет никакого способа вернуться и исправить свою ошибку. Одним из путей решения этой проблемы является принятие трансформационной стратегии. Трансформационные объединенные классификаторы работают путем создания первоначального присвоения меток для входов и последующего итеративного уточнения этого присвоения в попытке исправить несоответствия между связанными входами. Разметчик Брилля, описанный в (1), является хорошим примером этой стратегии.
Другим решением является назначение оценки для всех возможных последовательностей теги частей речи и выбор последовательности, общая оценка которой является самой высокой. Это подход, принятый Скрытыми моделями Маркова. Скрытые модели Маркова аналогичны последовательным классификаторам тем, что смотрят и на входы и на историю предсказанных меток. Однако они не просто находят единственную лучшую метку для данного слова, они генерируют распределение вероятностей по меткам. Эти вероятности затем объединяются для расчета оценки вероятности для последовательностей меток, и последовательность меток с наибольшей вероятностью выбирается. К сожалению, число возможных последовательностей меток достаточно велика. Для набор из 30 меток, есть около 600 триллион (3010) способов пометить предложение из 10 слов. Для того, чтобы избежать рассмотрения всех этих возможных последовательностей по отдельности, скрытые марковские модели требуют, чтобы экстрактор свойств смотрел только на самую последнюю метку (или на n самых последних меток, где n достаточно мало). Учитывая это ограничение, можно использовать динамическое программирование (4.7), чтобы эффективно найти наиболее вероятную последовательность меток. В частности, для каждого последовательного индекса слова i оценка вычисляется для каждой возможной текущей и предыдущей метки. Этот же базовый подход применяется двумя другими продвинутыми моделями, которые называются модели максимальной энтропии Маркова и линейно-цепные условные модели случайного поля; но другие алгоритмы используются для нахождения оценки последовательностей меток.
2 Другие примеры контролируемой классификации
2.1 Выделение предложения
Выделение предложения можно рассматривать как задачу классификации для пунктуации: всякий раз, когда мы сталкиваемся с символом, который мог бы положить конец предложения, такие как период или знак вопроса, мы должны решить, прекращает ли предыдущее предложение.
Первый шаг заключается в том, чтобы получить некоторые данные, которые уже были разделены на предложения и преобразовать их в форму, которая является подходящей для извлечения признаков:
|
Здесь tokens - это объединенный список токенов из отдельных предложений, а boundaries - набор, содержащий индексы всех токенов на границе предложений. Далее нам необходимо указать свойства данных, которые будут использоваться для решения вопроса о том, указывает ли пунктуация на границу предложения:
|
На основе этого экстрактора свойств, мы можем создать список помеченных наборов свойств, выбрав все токены пунктуации и пометив, являются ли они граничными токенами или нет:
|
С помощью этих наборов свойств, мы можем обучить и оценить классификатор пунктуации:
|
Чтобы использовать этот классификатор для выделения предложений, мы просто проверяем каждый знак препинания на предмет того, помечен ли он как граница; и разделяем список слов на знаках, являющихся границами предложений. Листинг в 2.1 показывает, как это можно сделать.
| ||
Пример 2.1 (code_classification_based_segmenter.py): Листинг 2.1: Выделитель предложений основанный на классификации |
2.2 Определение типов акта диалога
При обработке диалога может быть полезно думать о высказываниях как о типе действия, выполняемого говорящим. Эта интерпретация наиболее очевидна для перформативных высказываний, таких как "Я прощаю тебя" или "Держу пари, вы не сможете подняться на этот холм". Но приветствия, вопросы, ответы, утверждения и уточнения - все могут рассматриваться как типы основанных на речи действий. Признание актов диалога, лежащих в основе высказываний в диалоге, может стать важным первым шагом в понимании беседы.
NPS Chat Corpus, который был продемонстрирован в 1, состоит из более чем 10.000 сообщений из сеансов обмена мгновенными сообщениями. Все эти сообщения были помечены одним из 15 типов акта диалога, такими как "Заявление", "Эмоция", "Вопрос" и "Продолжение". Поэтому мы можем использовать эти данные, чтобы построить классификатор, который может идентифицировать типы акта диалога для новых мгновенных сообщений. Первым шагом является извлечение основных данных сообщений. Мы вызовем xml_posts(), чтобы получить структуру данных, представляющую XML аннотацию для каждой записи:
|
Далее мы определим простой экстрактор свойств, который проверяет, какие слова содержит сообщение:
|
Наконец, мы построим данные обучения и тестирования путем применения экстрактор свойств для каждого сообщения (используя post.get('class') для получения типа акта диалога) и создадим новый классификатор:
|
2.3 Признание текстового воплощения
Признание текстового воплощения (ПТВ (RTE)) - это задача определения того, влечет ли за собой данный фрагмент текста T другой текст, который называется "гипотезой" (как уже обсуждалось в 5). До сегодняшнего дня было четыре RTE проблемы с доступными для конкурирующих команд данными для разработки и тестирования. Вот несколько примеров пар текст/гипотеза из набора данных разработки проблемы №3. Метка Истина указывает на то, что воплощение есть, а Ложь на то, что его нет.
Задача 3, пара 34 (Истина)
Т: Парвиз Давуди представлял Иран на встрече Шанхайской организации сотрудничества (ШОС), формирующейся ассоциации, которая связывает вместе Россию, Китай и четыре бывших советских республик Средней Азии для борьбы с терроризмом.
Г: Китай является членом ШОС.
Задача 3, пара 81 (Ложь)
Т: В соответствии с уставом организации NC членами ООО являются Г. Нэльсон Биверс, ИИИ, Г. Честер Биверс и Дженни Биверс Стюарт.
Г: Jennie Биверс Стюарт является акционером Аналитической лаборатории Королины.
Следует подчеркнуть, что не предполагается, что связь между текстом и гипотезой должна быть логической реализацией, скорее речь идет о том, сделает ли человек вывод, что текст содержит разумные доказательства для принятия гипотезы в качестве истины.
Мы можем относиться к RTE как классификационной задаче, в которой мы пытаемся предсказать True/False метку для каждой пары. Хотя вполне вероятно, что успешные подходы к решению этой задачи будут включать сочетание синтаксического разбора, семантики и знаний реального мира, многие ранние попытки RTE достигли достаточно хороших результатов с помощью неглубокого анализа на основе сходства текста и гипотезы на уровне слов. В идеальном случае мы бы ожидали, что если есть воплощение, то вся информация, выраженная гипотезой, должна также присутствовать в тексте. И наоборот, если есть информация, содержащаяся в гипотезе, которая отсутствует в тексте, то воплощения не будет.
В нашем детекторе свойств RTE (2.2), мы позволили словам (т.е. типам слов) служить в качестве представителя информации, а наши свойства подсчитывают степень совпадения слов и степень, до которой слова есть в гипотезе, но не в тексте (схваченная методом hyp_extra()). Не все слова одинаково важны - упоминания именованных субстанций, таких как имена людей, организаций и мест, вероятно, будут более значительными, что побуждает нас извлечь четкую информацию для wordS и neS (именованных субстанций). Кроме того, некоторые высокочастотные функциональные слова отфильтровываются как "стоп-слова".
| [xx] | дать некоторое вступление к RTEFeatureExtractor?? |
| ||
Пример 2.2 (code_rte_features.py) : Листинг 2.2: Экстрактор свойств для "Признания текстового воплощения" . Класс RTEFeatureExtractor создает мешок слов для текста и гипотезы после отбрасывания некоторых стоп-слов, затем вычисляет совпадения и различия. |
Чтобы проиллюстрировать содержание этих свойств, мы рассмотрим некоторые атрибуты Пары текста/гипотезы №34, показанной ранее:
|
Эти свойства указывают, что все важные слова в гипотезе содержатся в тексте, и, таким образом, есть некоторое оправдание для маркировки этой пары как Истины.
Модуль nltk.classify.rte_classify достигает точности чуть более 58% на комбинированных тестовых данных RTE с помощью таких методов. Хотя эта цифра не очень впечатляет, требуются значительные усилия и больше лингвистической обработки, чтобы значительно улучшить результаты.
2.4 Увеличение масштаба до больших наборов данных
Python предоставляет отличную среду для выполнения базовых операций обработки текста и извлечения свойств. Однако он не способен выполнить интенсивные численные вычисления, требуемые методами машинного обучения столь же быстро, как языки низкого уровня, как C. Поэтому, если вы попытаетесь использовать чисто питоновские реализации машинного обучения (например, NLTK.NaiveBayesClassifier) на больших наборах данных, вы можете обнаружить, что алгоритму обучения требуется необоснованно большое количество времени и памяти для завершения.
Если вы планируете обучать классификаторы с помощью большого количества обучающих данных или большому количеству свойств, мы рекомендуем вам изучить возможности NLTK для взаимодействия с внешними пакетами машинного обучения. После того, как были установлены эти пакеты, NLTK может прозрачно вызывать их (с помощью системных вызовов) для обучения моделей классификаторов значительно быстрее, чем чисто питоновские реализации. Посетите веб-страницу NLTK для получения списка рекомендуемых пакетов машинного обучения, которые поддерживаются NLTK.
3 Оценка
Для того, чтобы решить, точно ли классификационная модель схватывает паттерн, мы должны оценить эту модель. Результат этой оценки важен для принятия решения о том, насколько модель заслуживает доверие, и для каких целей мы можем ее использовать. Оценка также может быть эффективным инструментом для будущих усовершенствований модели.
3.1 Тестовый набор данных
Большинство методов оценки рассчитывают балл модели путем сравнения меток, которые она генерирует для входов в тестовом наборе (или оценочном наборе) с правильными метками для этих входов. Этот тестовый набор, как правило, имеет такой же формат, как и обучающий набор. Однако очень важно, чтобы тестовый набор отличался от учебного корпуса: если бы мы просто повторно использовали учебный набор в качестве тестового набора, то модель, которая просто запомнили свой вход, без обучения тому, как обобщить учебный набор для новых примеров, мы бы получили обманчиво высокий балл.
При построении тестового набора, зачастую существует компромисс между количеством данных доступных для тестирования и количеством данных доступных для обучения. Для задач классификации, которые имеют небольшое количество хорошо сбалансированных меток и разнообразный тестовый набор, значимая оценка может быть выполнена с помощью всего лишь 100 экземпляров оценки. Но если задача классификации имеет большое количество меток или включает в себя очень редкие метки, то размер тестового набора должен быть выбран таким образом, чтобы гарантировать, что наименее частая метка встречается по меньшей мере 50 раз. Кроме того, если тестовый набор содержит множество тесно связанных экземпляров - таких, как экземпляры, выбираемые из одного документа - то размер тестового набора должен быть увеличен, чтобы гарантировать, что это отсутствие разнообразия не искажает результаты оценки. Когда доступно большое количество аннотированных данных, обычное дело заблуждаться "на стороне безопасности" используя 10% от общего объема данных для оценки.
Еще одно соображение при выборе тестового набора - это степень сходства между экземплярами в тестовом наборе и наборе разработки. Чем более схожи эти два набора данных, тем менее уверенными мы можем быть, что результаты оценки будут обобщать результаты на других наборах данных. Например, рассмотрим задачу частеречной разметки. На одном полюсе мы могли бы создать обучающий набор и тестовый набор, назначая в случайном порядке предложения из источника данных, который отражает единственный жанр (новости):
|
В этом случае наш тестовый набор будет очень похож на наш тренировочный набор. Обучающий набор и набор для тестирования взяты из одного и того же жанра, поэтому мы не можем быть уверены в том, что результаты оценки будут обобщать результаты для других жанров. Что еще хуже, из-за вызова random.shuffle(), тестовый набор содержит предложения, которые взяты из тех же документов, которые были использованы для обучения. Если есть какая-либо закономерность в пределах документа - скажем, если данное слово появляется с определенной меткой части речи особенно часто - то эта особенность будет отражена как в наборе разработки, так и в тестовом наборе. Несколько лучший подход состоит в том, чтобы тренировочный и тестовый набор были взяты из различных документов:
|
Если мы хотим выполнить более жесткие оценки, мы можем составить тестовый набор из документов, которые менее тесно связаны с документами в тренировочном наборе:
|
Если мы построим классификатор, который хорошо работает на этом тестовом наборе, то мы можем быть уверены в том, что он имеет способность хорошо обобщать далеко за пределами данных, на которых он был обучен.
3.2 Точность
Наиболее простой показатель, который может быть использован для оценки классификатора, точность, измеряет процент входов в тестовом наборе, которые были правильно помечены классификатором. Например, классификатор пола имени, который предсказывает правильное название 60 раз в тестовом наборе, содержащем 80 имен, будет иметь точность 60/80 = 75%. Функция nltk.classify.accuracy() рассчитает точность модели классификатора на данном тестовом наборе:
|
При интерпретации балла точности классификатора важно учитывать частоты меток отдельных классов в тестовом наборе. Например, рассмотрим классификатор, который определяет правильно смысл слова для каждого вхождения слова bank. Если мы оцениваем этот классификатор по тексту финансовой ленте новостей, то мы можем обнаружить, что значение финансовое учреждение появляется 19 раз из 20. В этом случае точность 95% вряд ли впечатляет, так как мы могли бы достичь такой точности с моделью, которая всегда возвращает значение финансовое учреждение. Однако, если мы напротив оцениваем классификатор на более сбалансированном корпусе, где самое распространенное значение слова имеет частоту 40%, тогда 95% оценка точности будет гораздо более позитивный результат. (Аналогичная проблема возникает при измерении согласия между аннотаторами в 2.)
3.3 Точность и охват
Другой случай, когда баллы точности могут ввести в заблуждение, - задачи "поиска", такие как поиск информации, где мы пытаемся найти документы, которые имеют отношение к конкретной задаче. Поскольку число несоответствующих документов значительно превышает число соответствующих документов, оценка точности модели, которая маркирует каждый документ как несоответствующий была бы очень близка к 100%.
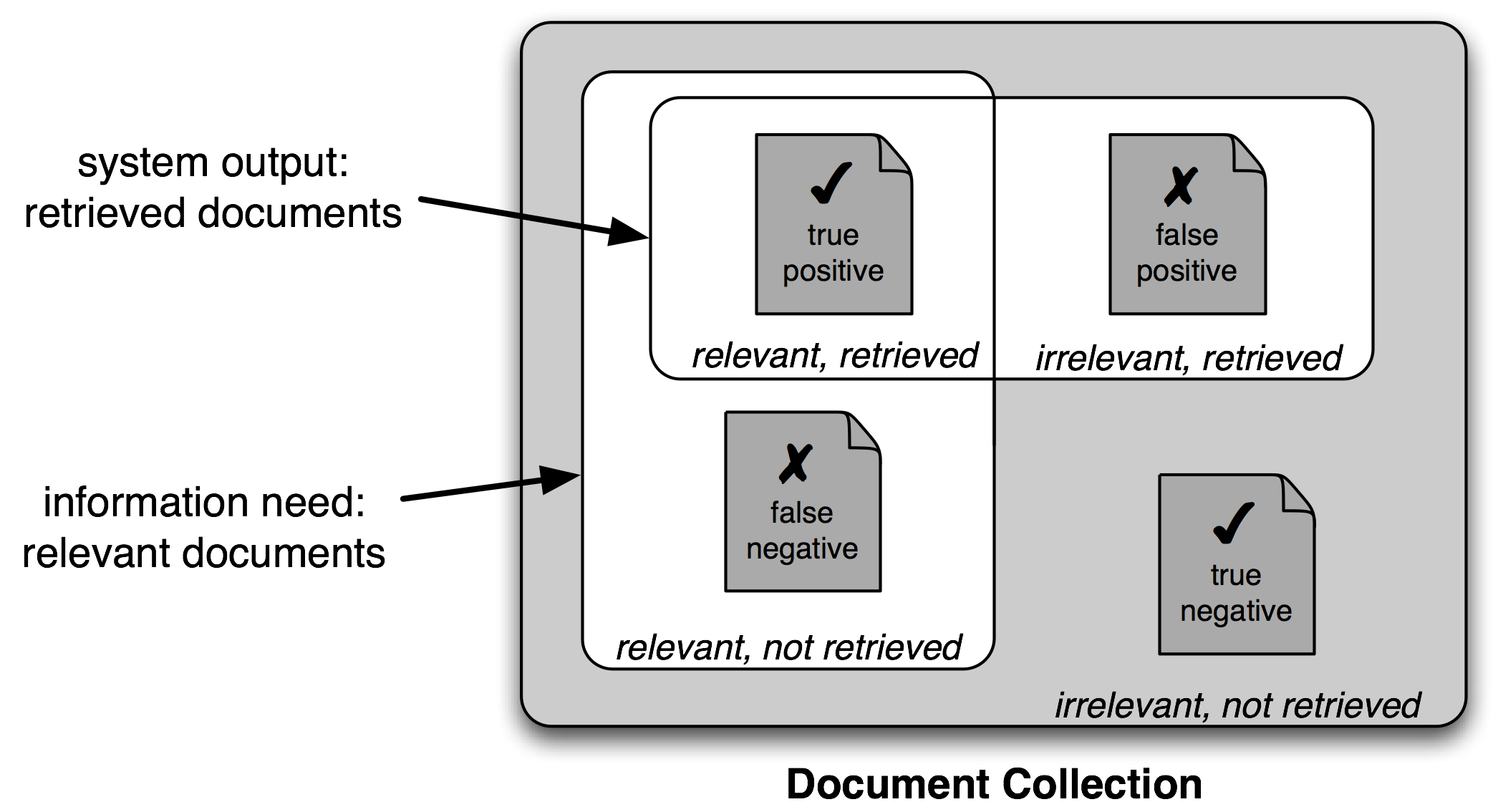
Рисунок 3.1: Истинные и ложные позитивы и негативы
Поэтому обычно используется другой набор мер для задач поиска, основанный на количестве элементов в каждой из четырех категорий, показанных на Рисунке 3.1:
- Истинные позитивы - это релевантные элементы, которые мы правильно определили как релевантные.
- Истинные негативы - это нерелевантные элементы, которые мы правильно определили как нерелевантные.
- Ложные позитивы (или Тип I ошибки) - это нерелевантные элементы, которые мы неправильно идентифицировали как релевантные.
- Ложные негативы (или Тип II ошибки) - это релевантные элементы, которые мы неправильно идентифицировали как нерелевантные.
Учитывая эти четыре числа, мы можем определить следующие показатели:
- Точность, которая указывает на то, сколько элементов, которые мы определили, были релевантны, TP/(TP + FP).
- Охват, который указывает, сколько релевантных элементов мы идентифицировали TP/(TP+FN).
- F-Мера (или F-балл), который сочетает в себе точность и охват, чтобы выразить единый балл, определяется как среднее гармоническое точности и охвата: (2×Точность×Охват)/(Точность + Охват).
3.4 Матрицы ошибок
При выполнении задач классификации с более, чем тремя метками, может быть информативным подразделять ошибки, сделанные моделью, по типу ошибки. Матрица ошибок представляет собой таблицу, где каждая ячейка [i, j] указывает на то, как часто метка j была предсказана, когда правильной был метка i. Таким образом, диагональные элементы (т.е. ячейки |ii|) указывают на метки, которые были предсказаны правильно, а недиагональные элементы указывают на ошибки. В следующем примере мы создаем матрицу ошибок для биграмм-разметчика, разработанного в 4:
|
Матрица ошибок показывает, что наиболее часто встречающиеся ошибки включают замену NN на JJ (для 1,6% слов) и NN на NNS (для 1,5% слов). Обратите внимание, что точки (.) указывают на ячейки, значение которых равно 0, а диагональные элементы - которые соответствуют правильным классификациям - отмечены угловыми скобками. .. XXX объясняет использование "референса" в приведенной выше легенде.
3.5 Перекрестная проверка
Для того, чтобы оценить наши модели, мы должны зарезервировать часть аннотированных данных для тестового набора. Как мы уже упоминали, если тестовый набор слишком мал, то наша оценка не может быть точной. Однако обычно увеличение тестового набора означает уменьшение учебного набора, что может оказать существенное влияние на результативность, если ограниченное количество аннотированных данных доступно.
Одним из решений этой проблемы является выполнение нескольких оценок на различных тестовых наборах и объединение баллов от этих оценок - метод, известный как перекрестная проверка. В частности, мы делим оригинальный корпус на N наборов, называемых складками. Для каждой из этих складок мы готовим модель, используя все данные за исключением данных в этой складке, а затем проверяем эту модель в этой складке. Даже если отдельные складки возможно слишком маленькие, чтобы дать точные баллы оценки сами по себе, комбинированный балл оценки основан на большом количестве данных, поэтому вполне надежен.
Второе и не менее важное преимущество использования кросс-проверки является то, что она позволяет нам исследовать, насколько широко результативность варьируется в зависимости от различных наборов обучения. Если мы получим очень похожие оценки для всех обучающих наборов N, то мы можем быть достаточно уверены в том, что оценка является точной. С другой стороны, если баллы оценки для каждого из N учебных наборов сильно отличаются, то нам, вероятно, следует скептически относиться к точности оценочного балла.
4 Деревья решений
В следующих трех разделах мы подробнее рассмотрим три метода машинного обучения, которые могут быть использованы для автоматического построения классификационных моделей: деревьев решений, наивных классификаторов Байеса и классификаторов максимальной энтропии. Как мы уже видели, можно рассматривать эти методы обучения, как черные ящики, просто модели обучения и использовать их для прогнозирования, не понимая, как они работают. Но многое можно узнать из более пристального взгляда на то, как эти методы обучения выбирают модели на основе данных в тренировочном наборе. Понимание этих методов может помочь нам выбрать соответствующие свойства, а особенно помочь нам решить, каким образом эти свойства должны быть закодированы. А понимание созданных моделей может позволить нам извлечь информацию о том, какие свойства являются наиболее информативными, и как эти свойства связаны друг с другом.
Дерево решений представляет собой простую блок-схему алгоритма, который выбирает метки для входных значений. Эта блок-схема состоит из узлов решений, которые проверяют значения свойств, и листовых узлов, которые присваивают метки. Чтобы выбрать метку для значения ввода, мы начинаем с первого узла решения на блок-схеме, известного как ее корневой узел. Этот узел содержит условие, которое проверяет одно из свойств входного значения и выбирает ветку на основе значения этого свойства. Следуя за веткой, которая описывает наше входное значение, мы прибываем к новому узлу решения с новым условием на свойство входного значения. Мы продолжаем следовать по ветвям, выбранным по условию каждого узла, пока мы не придем к листовому узлу, который предоставляет метку для входного значения. 4.1 показывает пример модели дерева решений задачи определения половой принадлежности имени.
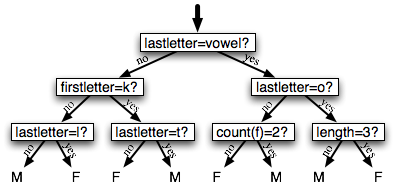
Рисунок 4.1: Модель дерева решений для задачи определения половой принадлежности имени. Обратите внимание, что диаграммы деревьев обычно рисуются "вверх ногами" с корнем наверху, а листьями внизу.
После того, как у нас есть дерево решений, несложно использовать ее для присвоения меток новым значениям ввода. Менее очевидно то, как мы можем построить дерево решений, которое моделирует данный обучающий набор. Но прежде чем мы рассмотрим алгоритм обучения для построения деревьев решений, мы рассмотрим более простую задачу: выбор лучшего "пня решения" для корпуса. Пень решения - это дерево решений с одним узлом, который решает, как классифицировать входы на основе единственного свойства. Он содержит один лист для каждого возможного значения свойства, указывая метку класса, которая должна быть назначена входу, свойство которого имеет это значение. Для того, чтобы построить пень решения, мы должны сначала решить, какие свойства должны быть использованы. Самый простой способ - построить пень решения для каждого возможного свойства и посмотреть, какой из них достигает наивысшей точности на обучающих данных, хотя есть и другие альтернативы, которые мы обсудим ниже. После того, как мы выбрали свойство, мы можем построить пень решения путем присвоения метки для каждого листа на основе наиболее частой метки для выбранных примеров в обучающем наборе (т. е. примеров, когда выбранное свойство имеет это значение).
Имея алгоритм выбора пней решения, несложно построить алгоритм для выращивания больших деревьев решений. Мы начнем с выбора наилучшего пня решения в целом для классификационной задачи. Затем мы проверим точность каждого из листьев на тренировочном наборе. Листья, которые не достигают достаточной точности, затем заменяются новыми пнями решений, подготовленными на подмножестве учебного корпуса, который определяется путем к листу. Например, мы могли бы вырастить дерево решений в 4.1, заменив крайний левый лист новым пнем решения, обученным на подмножестве имен из тренировочного набора, которые не начинаются с «k» или заканчиваются на гласную или "l".
4.1 Энтропия и информационный выигрыш
Как уже упоминалось ранее, существует несколько методов для определения наиболее информативного свойства для пня решения. Один из популярных вариантов, который называется информационный выигрыш, измеряет, насколько более организованными становятся входные значения, когда мы разделяем их, используя данное свойство. Для того, чтобы определить, насколько дезорганизован исходный набор входных значений, мы вычисляем энтропию их меток, которая будет высокой, если входные значения имеют весьма разнообразные метки, и низким, если много входных значений имеют одинаковую метку. В частности, энтропия определяется как сумма вероятностей всех меток умноженных на логорифм вероятности той же метки по основанию 2:
| (1) | H = −Σl |in| labelsP(l)×log2P(l). |
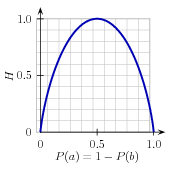
Рисунок 4.2: Энтропия меток в задаче предсказания пола имени в зависимости от процентного содержания мужских имен в данном наборе.
Например, 4.2 показывает, как энтропия меток в задаче предсказания половой принадлежности имени зависит от соотношения мужских и женских имен. Обратите внимание, что если большинство входных значений имеют одинаковую метку (например, если Р(мужское) близок к 0 или около 1), то энтропия мала. В частности, метки, которые имеют низкую частоту, не вносят большой вклад в энтропию (так как Р(l) мало) и метки с высокой частотой не вносят большой вклад в энтропию (так как log2P(l) мало). С другой стороны, если входные значения имеют большое разнообразие меток, тогда есть много меток со "средней" частотой, где ниР(l), ни log2P(l) не малы, поэтому энтропия высокая. 4.3 показывает, как вычислить энтропию списка меток.
| ||
| ||
Пример 4.3 (code_entropy.py) : Рисунок 4.3: Расчет энтропии Список меток |
После того, как мы рассчитали энтропию исходного набора меток входных значений, мы можем определить, насколько более организованными стали метки после применения пня решения. Для этого мы вычисляем энтропию для каждого из листьев пня решения и берем среднее значение величин энтропии этих листьев (взвешенных по количеству образцов в каждом листе). Информационный выигрыш тогда равен разности между величинами исходной и новой, уменьшенной энтропии. Чем больше информационная выгода, тем лучше пень решения выполняет работу по разделению входных значений на целостные группы, поэтому мы можем строить деревья решений путем выбора пней решений с самым высоким информационным выигрышем.
Еще одно соображение относительно деревьев решений - это эффективность. Простой алгоритм выбора пней решений, описанный выше, должен построить кандидата на пень решения для каждого возможного свойства, и этот процесс должен быть повторен для каждого узла в построенном дереве решений. Ряд алгоритмов были разработаны, чтобы сократить время на обучение за счет хранения и повторного использования информации о ранее оцененных примерах.
Деревья решений имеют ряд полезных качеств. Начнем с того, что они просты для понимания и их легко интерпретировать. Это особенно актуально в верхней части дерева решений, где алгоритм обучения обычно может найти очень полезные свойства. Деревья решений особенно хорошо подходят для случаев, когда могут быть сделаны многие иерархические категориальные различия. Например, деревья решений могут быть очень эффективными для схватывания филогенетических деревьев.
Однако деревья решений также имеют несколько недостатков. Одной из проблем является то, что, так как каждая ветвь в дереве решений расщепляет тренировочные данные, количество тренировочных данных доступных для подготовки нижних узлов дерева может стать недостаточным. В результате эти нижние узлы решений могут
переучиться на тренировочном наборе, извлекая паттерны, которые отражают характерные особенности обучающего набора, а не лингвистически значимые закономерности базовой проблемы. Одно из решений этой проблемы состоит в том, чтобы остановить деление узлов как только количество обучающих данных становится слишком мало. Другим решением является вырастить полное дерево решений, но потом подрезать узлы решений, которые не улучшают результативность на тестовом наборе разработки.
Вторая проблема с деревьями решений заключается в том, что они навязывают определенную последовательность проверки свойств, даже когда они могут действовать относительно независимо друг от друга. Например, при классификации документов по темам (таким как спорт, автомобилестроение или загадочные убийства), свойства, такие как hasword(football) являются весьма показательными для конкретной метки независимо от того, каковы другие значения свойства. Так как в верхней части дерева решений пространство ограничено, большинство из этих свойств должны повторяться на многих других ветвях дерева. А так как число ветвей увеличивается в геометрической прогрессии по мере продвижения вниз по дереву, количество повторений может быть очень большим.
Связанная с этим проблема заключается в том, что деревья решений не очень хорошо используют свойства, которые слабо предсказывают правильную метку. Так как эти свойства делают относительно небольшие постепенные улучшения, они, как правило, возникают очень низко в дереве решений. Но к тому времени, как обучающий компонент спустился достаточно глубоко, чтобы использовать эти свойства, уже нет достаточного количества тренировочных данных, чтобы достоверно определить, какой эффект они должны иметь. Если бы мы могли вместо этого посмотреть на эффект этих свойств на всем тренировочном наборе, то мы могли бы сделать некоторые выводы о том, как они должны влиять на выбор метки.
Тот факт, что деревья решений требуют, чтобы свойства проверялись в определенном порядке, ограничивает их способность использовать свойства, которые являются относительно независимыми друг от друга. Наивный метод классификации Байеса, который мы обсудим далее, преодолевает это ограничение, позволяя всем свойствам действовать "параллельно".
5 Наивные классификаторы Байеса
В наивных классификаторах Байеса каждая функция получает право голоса в определении того, какие метки должны быть отнесены к заданному входному значению. Чтобы выбрать метку для входного значения, наивный байесовский классификатор начинает с вычисления априорной вероятности каждой метки, которая определяется путем проверки частоты каждой метки в обучающем наборе. Вклад каждой метки затем объединяется с этой априорной вероятностью, чтобы прийти к оценке правдоподобия для каждой метки. Метка, чья оценка вероятности, является наивысшей затем присваивается входному значению. 5.1 иллюстрирует этот процесс.
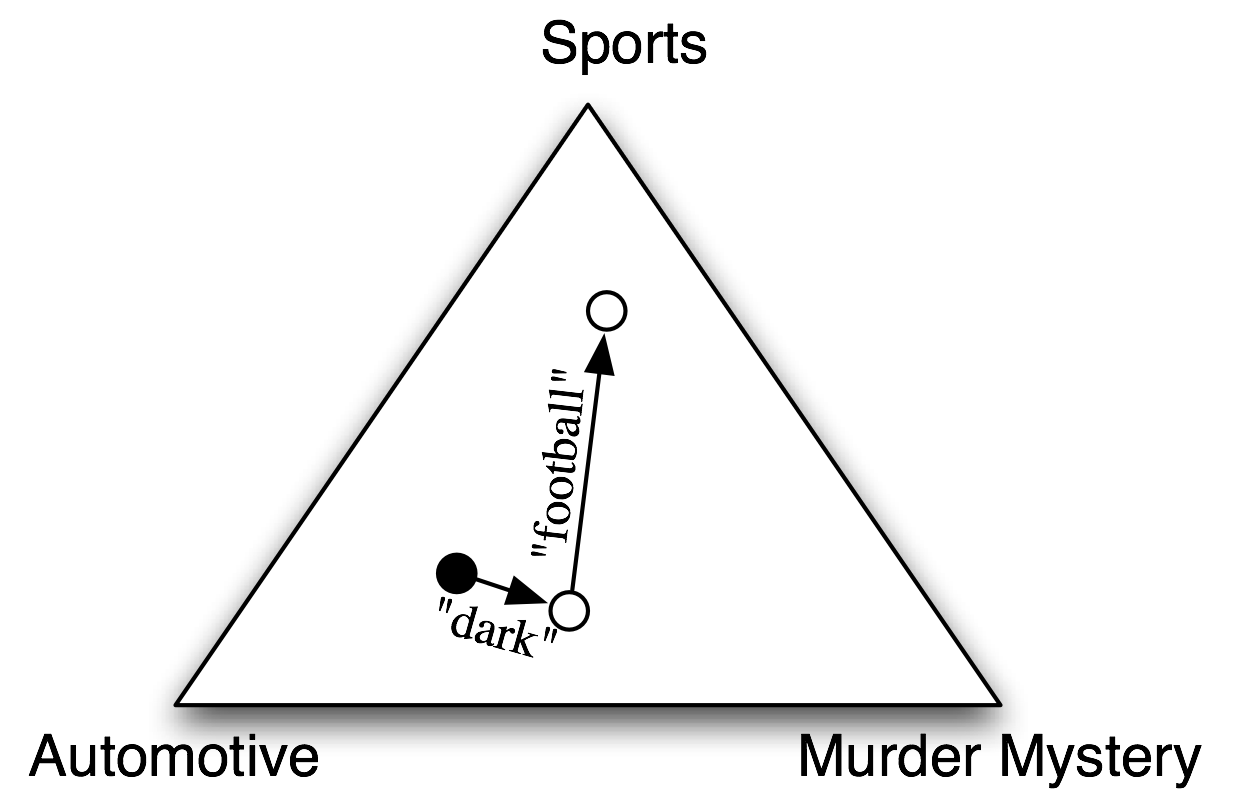
Рисунок 5.1: абстрактная иллюстрация процедуры, используемой наивным байесовским классификатором, чтобы выбрать тему для документа. В учебном корпусе большинство документов посвящено автомобилестроению, поэтому классификатор начинает в точке, расположенной ближе к "автомобильной" метке. Но затем он учитывает влияние каждого свойства. В этом примере входной документ содержит слово "темный", которое является слабым показателем загадочных убийств, но он также содержит слово "футбол", которое является сильным индикатором для спортивных документов. После того, как каждое свойство внесло свой вклад, классификатор проверяет, к какой метке он ближе всего, и присваивает эту метку входу.
Индивидуальные свойства вносят свой вклад в общее решение путем "голосования против" меток, которые не встречаются с этим свойством очень часто. В частности, оценка правдоподобия для каждой метки уменьшается путем умножения на вероятность того, что входное значение с этой меткой будет иметь это свойство. Например, если слово run возникает в 12% спортивных документов, 10% документов о загадочных убийствах и 2% автомобильных документов, то оценка вероятности для спортивной метки будет умножаться на 0,12; для метки загадочных убийств на 0,1, а для автомобильной метки будет умножена на 0,02. Общий эффект будет заключаться в уменьшении балла метки загадочных убийств чуть больше, чем балла спортивной метки, и значительном уменьшении балла автомобильной метки по отношению к двум другим меткам. Этот процесс проиллюстрирован на 5.2 и 5.3.
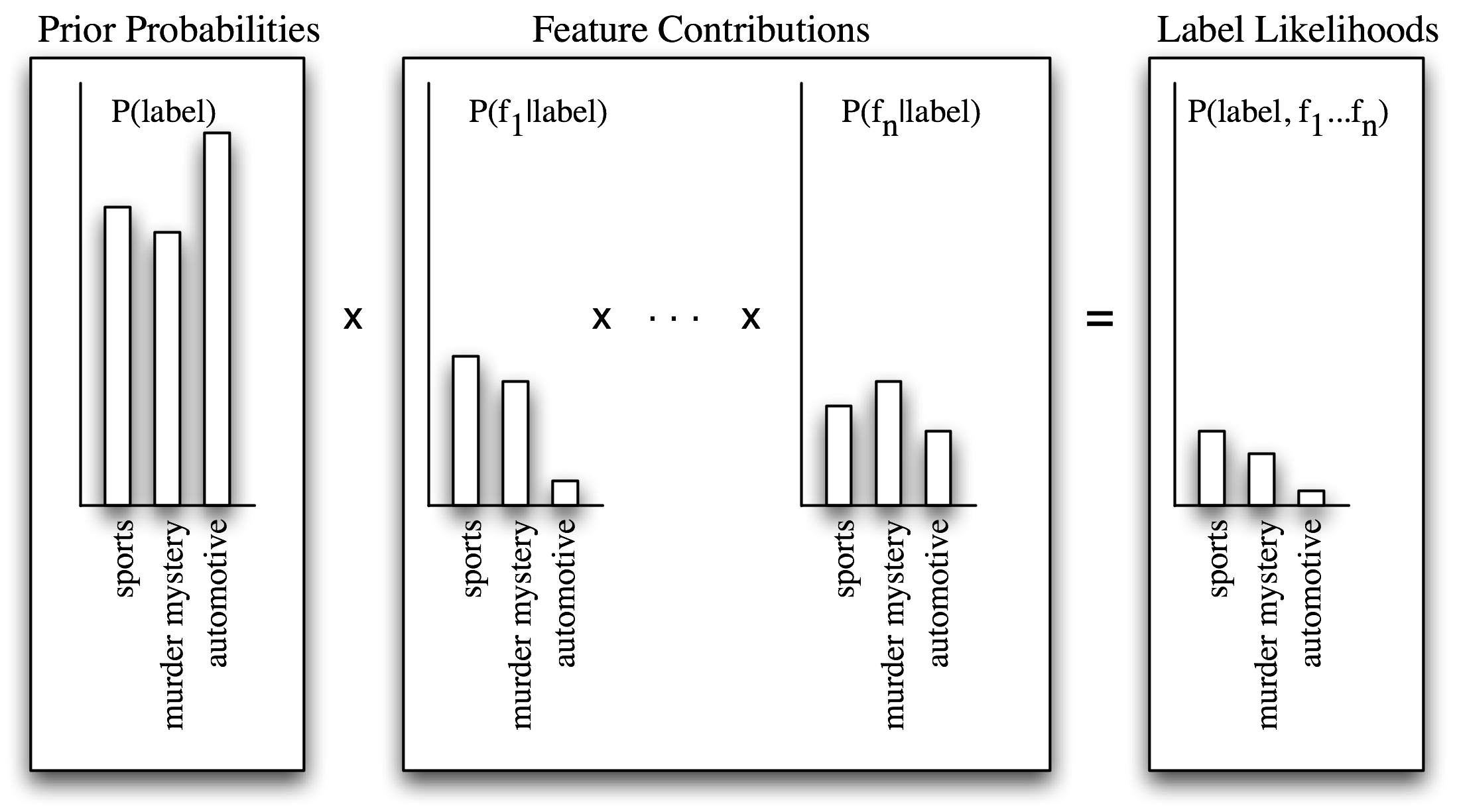
Рисунок 5.2: Расчет вероятностей меток с помощью наивного Байеса. Наивный Байеса начинает путем вычисления предварительной вероятности каждой метки, основываясь на том, как часто каждая метка встречается в обучающих данных. Каждое свойство затем вносит свой вклад в оценку вероятности для каждой метки путем умножения на вероятность того, что входные значения с этой меткой будут иметь это свойство. Результирующая оценка вероятности может рассматриваться как оценка вероятности того, что случайно выбранное значение из обучающего набора будет иметь как заданную метку, так и набор свойств, предполагая, что вероятности свойств являются независимыми.
5.1 Базовая вероятностная модель
Другой способ понимания наивного байесовского классификатора заключается в том, что он выбирает наиболее вероятную метку для входа, предполагая, что каждое входное значение генерируется сначала выбором метки класса для этого входного значения, а затем созданием каждого свойства, совершенно не зависимо от любого другого свойства. Конечно, это предположение нереально; свойства часто сильно зависят друг от друга. Мы вернемся к некоторым следствиям этого предположения в конце этого раздела. Это упрощающее предположение, известное как наивное байесовское предположение (или предположение независимости) делает гораздо проще объединение вклада различных свойств, так как нам не нужно беспокоиться о том, как они должны взаимодействовать друг с другом.
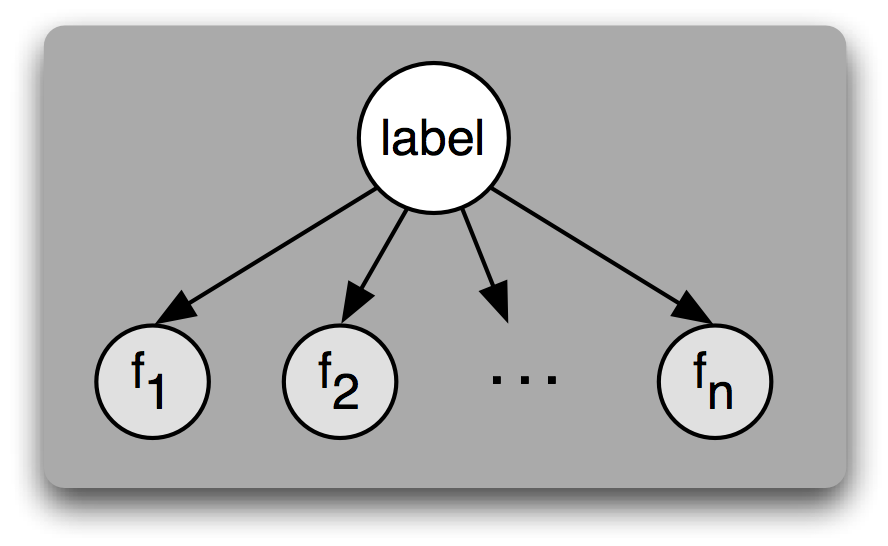
Рисунок 5.3: Байесовской сетевой график, иллюстрирующий генеративный процесс, который предполагается наивным байесовскоим классификатором. Для создания помеченного входа модель сначала выбирает метку для входа, затем генерирует каждое свойство входа на основе этой метки. Предполагается, что каждое свойство совершенно не зависит от любого другого свойства данной метки.
Исходя из этого предположения, можно вычислить выражение для P(метка | свойство), вероятность того, что вход будет иметь определенную метку при условии, что он имеет определенный набор свойств. Чтобы выбрать метку для нового входа, мы можем просто выбрать метку для нового входа l, которая максимизирует P(L | свойства).
Прежде всего, отметим, что P (метка | свойства) равна вероятности того, что вход имеет определенную метку и определенный набор свойств, деленной на вероятность того, что он имеет определенный набор свойств:
| (2) | В (метка | свойства) = В (свойства, метка) / В (свойства) |
Далее, мы замечаем, что P (свойства) будет одинаковым для каждого выбора метки, поэтому, если мы просто заинтересованы в нахождении наиболее вероятной метки, достаточно вычислить P (свойства, метка), которую мы будем называть вероятность метки.
Замечание
Если мы хотим произвести оценку вероятности для каждой метки, а не просто выбрать наиболее вероятную метку, то самый простой способ вычисления P (свойств) просто вычислить сумму для меток P (свойства, метка):
| (3) | В(свойства) = Σм в| метки В(свойства, метка) |
Вероятность метки может быть представлена как вероятность метки умноженная на вероятность свойств данной метки:
| (4) | В (свойства, метка) = В (метка) × В (свойства | метка) |
Кроме того, поскольку все свойства не зависят друг от друга (для данной метки), мы можем выделить вероятность каждого отдельного свойства:
| (5) | В (свойства, метка) = В (метка) × Prod с в | свойства В (с | метка)` |
Это именно то уравнение, которое мы обсуждали выше для вычисления вероятности метки: В (метка) является априорной вероятностью для данной метки, а каждый из В (с | метка) представляет собой вклад одного свойства в вероятность метки.
5.2 Нулевые количества и сглаживание
Самый простой способ вычислить В (с | метка), вклад свойства с в вероятность метки для метка, состоит в том, чтобы взять процент учебных экземпляров с данной меткой, которые также имеют данное свойство:
| (6) | В (с | метка) = кол-во (с, метка) / кол-во (метка) |
Однако этот простой подход может стать проблематичным, когда свойство никогда не появляется с заданной метки в обучающем наборе. В этом случае наша расчетная величина для В (с | метка) будет равна нулю, что приведет к нулевой вероятности метки для данной метки. Таким образом, входу никогда не будет присвоен эта метка независимо от того, насколько хорошо другие свойства подходят этой метке.
Основная проблема здесь заключается в нашем расчете В (с | метка), вероятности того, что вход будет иметь некоторое свойство для данной метки. В частности, только то, что мы не видели сочетание свойство / метка в тренировочном наборе, не означает, что это сочетание невозможно. Например, мы не видели никаких документов о загадочных убийствах, содержащих слово "футбол", но мы не хотели бы сделать вывод, что это такие документы не могут существовать.
Таким образом, несмотря на то, что кол-во (с, метка) / кол-во (метка) является хорошей оценкой для В (с | метка), если кол-во (с, метка) является относительно большим, эта оценка становится менее надежной, когда кол-во (с) становится меньше. Таким образом, при построении наивных моделей Байеса для вычисления В (с | метка), вероятности свойства для данной метки, мы обычно используем более сложные методы, известные как методы сглаживания. Так, например, Ожидаемая Оценка Правдоподобия для вероятности свойства данной метки добавляет базовые 0,5 к каждому значению кол-во (с, метка), а Растянутая Оценка использует растянутый корпус для вычисления отношения между частотами свойств и их вероятностями. Модуль nltk.probability обеспечивает поддержку широкого спектра методов сглаживания.
5.3 Небинарные свойства
Мы предположили, что каждое свойство бинарно, то есть, что каждый вход либо имеет свойство, либо нет. Свойства с небинарными значениями (например, цветовое свойство, которое может быть красным, зеленым, синим, белым или оранжевым) могут быть преобразованы в бинарные свойства путем замены их бинарными свойствам, такими как "цвет-красный". Числовые свойства могут быть преобразованы в двоичных свойства с помощью биннинга, который заменяет их такими свойствами, как "4 <х <6".
Другой альтернативой является использование методов регрессии для моделирования вероятностей числовых свойств. Например, если мы предположим, что функция высоты имеет колоколообразную кривую распределения, то мы могли бы оценить В (высота | метка) нахождением среднего значения и дисперсии высот входов для каждой метки. В этом случае B (c = д | метка) не будет фиксированным значением, но будет изменяться в зависимости от значения д.
5.4 Наивность независимости
Причина, по которой наивные классификаторы Байеса называют "наивным", заключается в том, что они необоснованно предполагают, что все свойства независимы друг от друга для данной метки. В частности, почти все реальные проблемы содержат свойства с различной степенью зависимости друг от друга. Если бы мы должны были избегать каких-либо свойств, которые зависят друг от друга, было бы очень трудно построить хорошие наборы свойств, которые обеспечивают необходимую информацию для алгоритма машинного обучения.
Так что же происходит, когда мы игнорируем предположение о независимости и используем наивный байесовский классификатор со свойствами, которые не являются независимыми? Одна из проблем заключается в том, что классификатор может прийти к "двойному счету" - эффекту сильно связанных свойств, толкающему классификатор ближе к данной метке, чем это оправдано.
Чтобы увидеть, как это может произойти, рассмотрим классификатор пола имени, который содержит два идентичных свойства, с1 и с2. Другими словами, с2 является точной копией с1 и не содержит новой информации. Когда классификатор рассматривает входной сигнал, он будет учитывать вклад и с1 и с2 при выборе того, какую метку выбрать. Таким образом, информационному содержанию этих двух свойств будет придано больше веса, чем оно заслуживает.
Конечно, мы обычно не строим наивные классификаторы Байеса, которые содержат два одинаковых свойства. Однако мы строим классификаторы, которые содержат свойства, которые зависят друг от друга. Например, свойства заканчивается-на(а) и заканчивается-на(гласную) зависят друг от друга, потому что если входное значение имеет первое свойство, то оно должна также иметь и второе. Из-за свойств подобных этим дублированная информация может иметь больший вес, чем это оправдано обучающим набором.
5.5 Причина двойного счета
Причиной проблемы двойного счета является то, что в процессе обучения, вклады свойств вычисляются по отдельности; а при использовании классификатора для выбора метки нового входа эти вклады свойств объединяются. Одно из решений поэтому заключается в том, чтобы рассмотреть возможные взаимодействия между вкладами свойств во время обучения. Тогда мы могли бы использовать эти взаимодействия для корректировки вкладов отдельных свойств.
Для того, чтобы сделать это более точным, мы можем переписать уравнение для расчета вероятности метки, выделяя вклад каждого свойства (или метки):
| (7) | В (свойства, метка) = w [метка] × Prod с | в | свойствах w [с, метка] |
Здесь w [метка] - это "стартовый счет" для данной метки, а w [с, метка] - вклад данного свойства в вероятность этикетки. Мы называем эти значения w [метка] и w [с, метка] параметрами, или весами для данной модели. Используя наивный алгоритм Байеса, мы устанавливаем каждый из этих параметров независимо друг от друга:
| (8) | w [метка] = В (метка) |
| (9) | ж [с, метка] = В (с | метка) |
Однако в следующем разделе мы рассмотрим классификатор, который рассматривает возможные взаимодействия между этими параметрами при выборе их значений.
6 Классификаторы основанные на максимальной энтропии
Классификатор Максимальной Энтропии использует модель, которая очень похожа на модель, используемую наивным байесовским классификатором. Но вместо того, чтобы использовать вероятности для установки параметров модели, он использует методы поиска, чтобы найти набор параметров, которые обеспечивают максимальную результативность классификатора. В частности, он ищет набор параметров, который максимизирует общая правдоподобность учебного корпуса, которая определяется как:
| 1:10 | P(features) = Σx |in| corpus P(label(x)|features(x)) |
Где P (label | featurs), вероятность того, что вход, свойства которого featurs будет иметь метку класса label, определяется следующим образом:
| (11) | P (label | features) = P (label, features) / Σ label P (label, features) |
Из-за потенциально сложных взаимодействий между эффектами связанных свойств, не существует способа непосредственного расчета параметров модели, которые максимизируют вероятность обучающего набора. Таким образом, классификаторы максимальной энтропии выбирают параметры модели с помощью методов итеративной оптимизации, которые инициализируют параметры модели случайными величинами, а затем многократно уточняют эти параметры, чтобы приблизить их к оптимальному решению. Эти итерационные методы оптимизации гарантируют, что каждое уточнение параметров будет приближать их к оптимальным значениям, но не обязательно предоставляют средства определения того, когда были достигнуты эти оптимальные значения. Поскольку параметры классификатора максимальной энтропии выбираются с помощью итерационных методов оптимизации, их обучение может занять много времени. Это особенно актуально, когда размер обучающего набора, число свойств и число меток - все большие.
Замечание
Некоторые итерационные методы оптимизации намного быстрее, чем другие. При обучении модели максимальной энтропии избегайте использования методов: Generalized Iterative Scaling (GIS) (Обобщенное Итерационное Масштабирование (ОИМ)) и Improved Iterative Scaling (IIS) (Улучшенное Итеративное Масштабирование (УИМ)), которые значительно медленнее, чем методы: Conjugate Gradient (CG) Сопрояженного Градиента (СГ) и BFGS оптимизации.
6.1 Модель максимальной энтропии
Модель классификатора на основе максимальной энтропии является обобщением модели, используемой наивным байесовским классификатором. Подобно наивной модели Байеса, классификатор максимальной энтропии вычисляет вероятность каждой метки при заданном значении входного значения путем перемножения параметров, которые применимы для входного значения и метки. Модель наивного классификатора Байеса определяет параметр для каждой метки, указав его априорную вероятность и параметр для каждой пары (свойство, метка) с указанием вклада индивидуальных свойств в вероятность метки.
В отличие от этого, модель классификатора максимальной энтропии оставляет пользователю решить, какие комбинации меток и свойств должны получать свои собственные параметры. В частности, можно использовать один параметр, чтобы связать свойство с более чем одной меткой; или связать более одного свойства с заданной меткой. Это иногда позволит модели "обобщать" некоторые различия между связанными метками или свойствами.
Каждая комбинация меток и свойств, которая получает свой собственный параметр называется совместным свойством. Обратите внимание, что совместные свойства - это особенности помеченных значений, в то время как (простые) свойства - это особенности непомеченых значений.
Замечание
В литературе, в которой описываются и обсуждаются модели максимальной энтропии, термин "свойства" часто относится к совместным свойства; а термин «контексты» относится к тому, что мы до сих пор называли (простыми) свойствами.
Как правило, совместные свойства, которые используются для построения модели максимальной энтропии, точно отражают те, которые используются наивной моделью Байеса. В частности, совместное свойство определено для каждой метки, что соответствует w[label], и для каждой комбинации (простого) свойства и метки, что соответствует w[f, label]. Для данных совместных свойств модели максимальной энтропии, оценка, которая присваивается метке для данного входа, - это просто произведение параметров, связанных с совместными свойствами, которые применяются к этому входу и метке:
| (12) | P (вход, метка) = Prod совместные функции (вход, этикетка) ш [совместное особенность] |
6.2 Максимизация Энтропия
Интуицией, которая мотивирует классификацию максимальной энтропии, является то, что мы должны построить модель, которая схватывает частоты отдельных совместных свойств не делая каких-либо необоснованных предположений. Пример поможет проиллюстрировать этот принцип.
Предположим, что нам поставлена задача выбора правильного слова для смысла данного слова из списка десяти возможных смыслов (помеченных A-J). Сначала нам ничего больше не сказали об этом слове или этих смыслах. Есть много распределения вероятностей, которые мы могли бы выбрать для десяти значений, таких как:
| A | B | C | D | E | F | G | H | I | J | |
|---|---|---|---|---|---|---|---|---|---|---|
| (i) | 10% | 10% | 10% | 10% | 10% | 10% | 10% | 10% | 10% | 10% |
| (ii) | 5% | 15% | 0% | 30% | 0% | 8% | 12% | 0% | 6% | 24% |
| (iii) | 0% | 100% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | Таблица 6.1 |
Хотя любое из этих распределений могло бы быть правильным, мы, скорее всего, чтобы выберем распределение (i), потому что без какой-либо дополнительной информации нет никаких оснований полагать, что какое-либо значение слова более вероятно, чем другое. С другой стороны, распределения (ii) и (iii) отражают предположения, которые не поддерживаются тем, что мы знаем.
Один из способов схватить эту интуицию, сообщающую что распределение (i) является более "справедливым", чем два других, - сослаться на понятие энтропии. При обсуждении деревьев решений мы описали энтропию как меру "дезорганизованности" набора меток. В частности, если одна метка доминирует, то энтропия мала, но если метки распределены более равномерно, то энтропия высока. В нашем примере мы выбрали распределение (i), так как вероятности его меток равномерно распределены, другими словами, так как его энтропия высока. В общем случае, принцип Максимальной Энтропии гласит, что среди распределений, которые согласуются с тем, что мы знаем, мы должны выбрать распределение, энтропия которого является самой высокой.
Далее, предположим, что нам говорят, что значение A появляется с частотой 55%. Опять же есть много распределений, которые согласуются с этой новой информацией, таких как:
| A | B | C | D | E | F | G | H | I | J | |
|---|---|---|---|---|---|---|---|---|---|---|
| (iv) | 55% | 45% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% |
| (v) | 55% | 5% | 5% | 5% | 5% | 5% | 5% | 5% | 5% | 5% |
| (vi) | 55% | 3% | 1% | 2% | 9% | 5% | 0% | 25% | 0% | 0% | Таблица 6.2 |
Но опять же, мы, скорее всего, выберем распределение, которое делает наименьшее количество необоснованных допущений - в данном случае распределение (v).
Наконец, предположим, что нам говорят, что слово «up» появляется в соседнем контекст 10% времени, и что, когда оно появляется в этом контексте, есть 80% вероятность того, что значение A или C будет использоваться. В этом случае мы придумать распределение "в ручную" будет труднее; однако мы можем убедиться, что следующее распределение выглядит соответствующим образом:
| A | B | C | D | E | F | G | H | I | J | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (vii) | +up | 5,1% | 0,25% | 2,9% | 0,25% | 0,25% | 0,25% | 0,25% | 0,25% | 0,25% | 0,25% |
| ` ` | -up | 49,9% | 4,46% | 4,46% | 4,46% | 4,46% | 4,46% | 4,46% | 4,46% | 4,46% | 4,46% | Таблица 6.3 |
В частности, распределение согласуется с тем, что мы знаем: если мы сложим вероятности в колонке А, мы получаем 55%; если сложить вероятности строки 1, мы получаем 10%; и если мы складываем ячейки для значений А и С в строке +up, мы получаем 8% (или 80% +up случаев). Кроме того, остальные вероятности "равномерно распределены".
На протяжении этого примера мы ограничились распределениями, которые согласуются с тем, что мы знаем; среди них мы выбрали распределение с самой высокой энтропией. Это именно то, что делает классификатор максимальной энтропии. В частности, для каждого совместного свойства модель максимальной энтропии вычисляет "эмпирическую частоту" этого свойства - т. е. частоту, с которой он встречается в обучающем наборе. Затем он осуществляет поиск распределения, которое максимизирует энтропию, в то же время предсказывая правильную частоту для каждого совместного свойства.
6.3 Генеративные против условных классификаторов
Важное различие между наивным байесовским классификатором и классификатором максимальной энтропии связано с типом вопросов, для ответа на которые они могут быть использованы. Наивный байесовский классификатор является примером порождающего классификатора, который строит модель, которая предсказывает P (input, label), совместную вероятность пары (вход, метка). Поэтому порождающие модели могут быть использованы, чтобы ответить на следующие вопросы:
- Какая метка является наиболее вероятной для данного входа?
- Насколько вероятна данная метка для данного входа?
- Каково наиболее вероятное значение входного сигнала?
- Насколько вероятно заданное значение входного сигнала?
- Насколько вероятно данное входное значение для данной метки?
- Какова наиболее вероятная метка для входа, который мог бы иметь одно из двух значений (но мы не знаем какое)?
Классификатор максимальной энтропии, с другой стороны, является примером условного классификатора. Условные классификаторы строят модели, предсказывающие P (label | input) - вероятность метки для данного входного значения. Таким образом, условные модели также могут быть использованы для ответа на вопросы 1 и 2. Однако условные модели не могут быть использованы, чтобы ответить на оставшиеся вопросы 3-6.
В целом порождающие модели строго мощнее условных моделей, так как мы можем вычислить условную вероятность В (метка | вход) от совместной вероятности В (вход, метка), но не наоборот. Однако эта дополнительная мощность поставляется по определенной цене. Поскольку модель является более мощной, она имеет более "свободные параметры", которые должны быть изучены. Однако размер обучающего набора фиксирован. Поэтому при использовании более мощной модели мы в конечном итоге оказываемся с меньшим количеством данных, чем может быть использовано для обучения, что делает труднее нахождение оптимальных значений параметров. В результате порождающая модель может работать не так хорошо при ответе на вопросы 1 и 2, как условная модель, так как условная модель может сосредоточить свои усилия на этих двух вопросах. Однако если нам действительно нужны ответы на такие вопросы, как 3-6, то у нас нет иного выбора, кроме как использовать порождающую модель.
Различие между порождающей моделью и условной моделью аналогична различию между топографической картой и изображением горизонта. Хотя топографическая карта может быть использована, чтобы ответить на более широкий круг вопросов, сформировать точную топографическую карту значительно труднее, чем создать точную линию горизонта.
7 Моделирование лингвистических паттернов
Классификаторы могут помочь нам понять языковые закономерности, которые возникают в естественном языке, позволяя нам создавать явные модели, которые схватывают эти закономерности. Как правило, эти модели используют контролируемые методы классификации, но также возможно построить аналитически мотивированные модели. В любом случае эти явные модели служат двум важным целям: они помогают нам понять языковые закономерности и они могут быть использованы для составления прогнозов о новых языковых данных.
Степень, в которой явные модели могут дать нам понимание языковых закономерностей, во многом зависит от того, какая модель используется. Некоторые модели, такие как деревья решений, являются относительно прозрачными и дают нам прямую информацию о том, какие факторы играют важную роль в принятии решений, и о том, какие факторы связаны друг с другом. Другие модели, такие как многоуровневые нейронные сети, гораздо более непрозрачны. Хотя получить некоторое представление, изучая их, возможно, как правило, это требует гораздо больше работы.
Но все явные модели могут делать прогнозы о новых "не виденных" данных языка, которые не были включены в корпус, использовавшийся для построения модели. Эти прогнозы могут быть оценены для определения точности модели. После того, как модель считается достаточно точной, она может быть использована, чтобы автоматически предсказывать информацию о новых языковых данных. Эти прогностические модели могут быть объединены в системы, которые выполняют множество полезных задач обработки языка, например, классификация документов, автоматический перевод и ответы на вопросы.
7.1 Что модели говорят нам?
Важно понять, что мы можем узнать о языке из автоматически построенной модели. Одним из важных моментов при работе с моделями языка является различие между описательными моделями и объясняющими моделями. Описательные модели схватывают закономерности в данных, но они не дают никакой информации о том, почему данные содержат эти закономерности. Например, как мы видели в разделе 3.1, синонимы absolutely и definitely не являются взаимозаменяемыми: мы говорим absolutely adore, а не definitely adore и definitely prefer, а не absolutely prefer. В противоположность этому, объясняющие модели пытаются схватить свойства и отношения, которые вызывают языковые закономерности. Например, мы могли бы ввести абстрактное понятие "полярного глагола", как такого, который имеет экстремальное значение, и классифицировать некоторые глаголы, как adore и detest, как полярные. Наша объясняющая модель содержала бы ограничение, что absolutely можно комбинировать только с полярными глаголами, а definitely можно комбинировать только с неполярными глаголами. Таким образом описательные модели предоставляют информацию о корреляциях в данных, в то время как объясняющие модели идут дальше, чтобы постулировать причинно-следственные связи.
Большинство моделей, которые автоматически построены из корпуса, являются описательными моделями; другими словами, они могут сказать нам, какие свойства имеют отношение к заданному паттерну или конструкции, но они не всегда могут сказать нам, как эти свойства и паттерны связаны друг с другом. Если наша цель состоит в том, чтобы понять языковые закономерности, то мы можем использовать эту информацию о том, какие свойства связаны, в качестве отправной точки для дальнейших экспериментов, сконструированных для выискивания отношений между свойствами и закономерностями. С другой стороны, если мы просто заинтересованы в использовании модели для прогнозирования (например, как части системы обработки языка), то мы можем использовать модель для составления прогнозов о новых данных, не заботясь о деталях лежащего в основе причинно-следственного отношения.
8 Резюме
- Моделирование лингвистических данных, находящихся в корпусе, может помочь нам понять языковые закономерности и может быть использовано для составления прогнозов о новых языковых данных.
- Контролируемые классификаторы используют помеченный тренировочный корпус для построения моделей, предсказывающих метку входа, основываясь на конкретных свойствах этого входа.
- Контролируемые классификаторы могут выполнять широкий спектр задач NLP, в том числе классификацию документов, частеречную разметку, выделение предложений, определение типа акта диалога, определение отношений воплощения и многие другие задачи.
- При обучении контролируемого классификатора, вы должны разделить корпус на три набора данных: учебный набор для построения модели классификатор; тестовый набор разработки для выбора и отладки свойств модели; и тестовый набор для оценки результативности конечной модели.
- При оценке контролируемого классификатора важно использовать свежие данные, которые не были включены в учебный или тестовый набор разработки. В противном случае ваши результаты оценки могут быть нереалистично оптимистичными.
- Деревья решений - это автоматически построенные, имеющие древовидную структуру блок-схемы, которые используются для присвоения меток для входных значений в зависимости от их свойств. Несмотря на то, что их легко интерпретировать, они не очень хороши для случаев, где значения свойств взаимодействуют при определении правильной метки.
- В наивных классификаторах Байеса каждое свойство самостоятельно вносит свой вклад в решение о том, какую следует использовать метку. Это позволяет значениям свойств взаимодействовать, но может быть проблематичным, когда два или несколько свойств в высокой степени коррелируют друг с другом.
- Классификаторы максимальной энтропии используют базовую модель, которая похожа на модели, используемые наивными Байеса; однако они применяют итерационную оптимизацию для поиска множества весов свойств, которые максимизируют вероятность обучающего набора.
- Большинство моделей, которые автоматически построены из корпуса, являются описательными - они позволяют нам узнать, какие свойства имеют отношение к данной модели или конструкции, но они не дают никакой информации о причинно-следственной связи между этими свойствами и закономерностями.
7 Дополнительные материалы
Пожалуйста, обратитесь к http://nltk.org/ для получения дополнительных материалов по этой главе, а также по тому, как установить внешние пакеты машинного обучения, такие как Weka, Mallet, TADM и MEGAM. Для получения большего количества примеров классификации и машинного обучения с помощью NLTK, пожалуйста, посмотрите HOWTOs по классификации на http://nltk.org/howto.
Для общего введения в область машинного обучения мы рекомендуем (Alpaydin, 2004). Для получения более математически интенсивного введения в теорию машинного обучения, см. (Hastie, Tibshirani, & Friedman, 2009). Отличные книги по использованию методов машинного обучения для НЛП включают в себя (Abney, 2008), (Daelemans & Bosch, 2005), (Feldman & Sanger, 2007), (Segaran, 2007), (Weiss et al, 2004). Более подробную информацию о методах сглаживания для языковых проблем см. в (Manning & Schutze, 1999). Более подробную информацию по моделированию последовательностей и особенно скрытым марковским моделям, см. в (Manning & Schutze, 1999) или (Jurafsky & Martin, 2008). Глава 13 (Manning, Raghavan, & Schutze, 2008) обсуждает использование наивного Байеса для классификации текстов.
Многие алгоритмы машинного обучения, обсуждаемые в этой главе, являются численно интенсивными, поэтому они будут работать медленно при кодировании их наивно на Python. Для получения информации о повышении эффективности численно интенсивных алгоритмов в Python, см. (Kiusalaas, 2005).
Методы классификации, описанные в этой главе, могут быть применены к очень широкому кругу проблем. Например, (Agirre & Edmonds, 2007) использует классификаторы для выполнения разрешение лексической неоднозначности; а (Melamed, 2001) использует классификаторы для создания параллельных текстов. Последние учебники, которые охватывают текстовую классификацию, включают в себя (Manning, Raghavan, & Schutze, 2008) и (Croft, Metzler, & Strohman, 2009).
Большая часть современных исследований в области применения методов машинного обучения к проблемам НЛП приводится в движение спонсируемыми правительством "вызовами", в рамках которых множеству научно-исследовательских организаций предоставляется один и тот же корпус разработки, с помощью которого они должны построить систему; после чего полученные системы сравниваются на основе зарезервированного тестового набора. Примеры этих соревнований включают CoNLL Shared Tasks, соревнования ACE, соревнования Признания Текстового Воплощения, а также соревнования AQUAINT. Обратитесь к http://nltk.org/ для получения списка указателей на веб-страницы этих задач.
10 Упражнения
☼ Читайте на одном из языковых технологий, указанных в данном разделе, например, слово смысловой неоднозначности, семантической классификации ролей, вопросов, отвечая, машинного перевода, названного обнаружения объекта. Узнайте, какой тип и количество аннотированных данных требуется для разработки таких систем. Почему вы думаете, требуется большое количество данных?
☼ При использовании любого из трех классификаторов, описанных в этой главе, и какие-либо функции вы можете думать, строить лучшее название гендерного классификатор вы можете. Начните путем разделения Имен Корпус на три подмножества: 500 слов для тестового набора, 500 слов для Дев-тестового набора, а остальные 6900 слов для тренировочного набора. Затем, начиная с примером имени гендерного классификатора, делают постепенные улучшения. Используйте DEV-тестовый набор, чтобы проверить ваши успехи. После того, как вы удовлетворены своей классификатор, проверить свою окончательную производительность на тестовом наборе. Как производительность на тестовом наборе по сравнению с исполнением на Dev-тестовом наборе? Это то, что можно было ожидать?
☼ Senseval 2 Корпус содержит данные, предназначенные для обучения разрешение лексической многозначности классификаторов. Он содержит данные для четырех слов: жесткий, интерес, линии, и служить. Выберите один из этих четырех слов, и загрузить соответствующие данные:
>>> От импорта nltk.corpus senseval >>> экземпляры = senseval.instances ( 'hard.pos') >>> Размер = INT (LEN (экземпляры) * 0.1) >>> train_set, test_set = экземпляры [размер:] экземпляры [: размер]
С помощью этого набора данных, построить классификатор, который предсказывает правильный смысл тег для данного экземпляра. См желтое HOWTO на http://nltk.org/howto для получения информации об использовании экземпляра объекты , возвращаемые Senseval 2 корпус.
☼ Использование обзора фильма документа классификатор обсуждается в этой главе, сформировать список из 30 признаков, что классификатор находит наиболее информативным. Можете ли вы объяснить, почему именно эти особенности являются информативными? Считаете ли вы какие-либо из них удивительно?
☼ Выберите одну из задач классификации, описанных в этой главе, такие как имя гендерного обнаружения, классификации документов, частеречная разметка, или диалоговом классификации акта. Используя ту же подготовку и тестовые данные, а также те же функции, экстрактор, построить три классификаторы для выполнения этой задачи: дерево решений, наивного байесовского классификатора, и классификатор максимальной энтропией. Сравните производительность трех классификаторов на выбранном Вами задачи. Как вы думаете, что ваши результаты могут отличаться, если вы использовали другую функцию экстрактор?
☼ синонимов сильный и мощный шаблон по- разному (попробуйте сочетая их с чипом и продаж). Какие особенности имеют существенное значение в этом различии? Построить классификатор, который предсказывает, когда каждое слово должно быть использовано.
◑ Диалог акт классификатор назначает метки на отдельные посты, не принимая во внимание контекст, в котором находится пост. Тем не менее, диалоговые акты в значительной степени зависят от контекста, и некоторые последовательности диалога действуют гораздо более вероятны, чем другие. Например, диалог акт ynQuestion гораздо больше шансов ответить на yanswer чем приветствие. Используйте этот факт, чтобы построить последовательный классификатор для маркировки диалоговых актов. Будьте уверены, чтобы рассмотреть, какие функции могут быть полезны. Смотрите код для последовательного классификатора для частичной из-тегов в речи 1.7 , чтобы получить некоторые идеи.
особенности ◑ Слово может быть очень полезно для выполнения классификации документов, так как слова, которые появляются в документе, дают четкое указание о том, что его семантическое содержание. Тем не менее, многие слова встречаются очень редко, а некоторые из наиболее информативных слов в документе и не может иметь место в наших обучающих данных. Одним из решений является сделать использование словарный запас, который описывает , как разные слова соотносятся друг с другом. Использование WordNet лексикон, увеличить обзорную фильм документа классификатор, представленные в этой главе, чтобы использовать функции, обобщающие слова, которые появляются в документе, что делает его более вероятно, что они будут соответствовать слова, найденные в обучающих данных.
★ ПП Приложение Корпус представляет собой корпус с описанием предложных решений фразы вложений. Каждый экземпляр в корпусе кодируется как объект PPAttachment:
>>> От импорта nltk.corpus ppattach >>> ppattach.attachments ( «обучение») [PPAttachment (отправленного = '0', глагол = 'присоединиться', noun1 = 'доска', преп = 'как', noun2 = ' директор ', вложение =' V '), PPAttachment (пересылаются =' 1 ', глагол =' является ', noun1 =' председатель ', преп =' о ', noun2 =' NV ', вложения =' N '),. ..] >>> INST = ppattach.attachments ( 'тренировка') [1] >>> (inst.noun1, inst.prep, inst.noun2) ( 'председатель', 'из', 'НВ')
Выберите только те случаи , когда inst.attachment является N:
>>> Nattach = [инст для инст в ppattach.attachments ( «обучения») ... если inst.attachment == 'N']
С помощью этого суб-корпус, построить классификатор, который пытается предсказать, какой предлог используется для подключения заданной пары существительных. Например, с учетом пары существительных "команда" и "исследователей" классификатор должен предсказать предлог "от". См желтое HOWTO на http://nltk.org/howto для получения дополнительной информации об использовании крепления корпус PP.
★ Предположим , вы хотите , чтобы автоматически генерировать описание прозы сцены, и уже было слово однозначно описать каждую сущность, например, банку, и просто хотел , чтобы решить , следует ли использовать или на в соотнесении различных предметов, например , книга в шкафу против книги на полке. Исследуйте этот вопрос, посмотрев на данные деянии; написание программ по мере необходимости.
| , ; ! |
|
Об этом документе ...
Обновлялся для NLTK 3.0. Это глава из книги Обработка естественного языка с помощью Python написанной Стивеном Бердом , Эваном Клайном и Эдвардом Лопером , Copyright © 2014 авторов. Он распространяется с Набором инструментов для естественного языка [http://nltk.org/], версия 3.0 в соответствии с условиями Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 Лицензии Соединенных Штатов [ http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
Этот документ был построен на ср 1 июля 2015 12:30:05 AEST