True Signal vs Correlated Null: Identifiability & Small Effects
Lei Sun
2017-03-29
Last updated: 2017-05-30
Code version: 9f7dd01
Illustration
n = 1e4
m = 5
set.seed(777)
zmat = matrix(rnorm(n * m, 0, sd = sqrt(2)), nrow = m, byrow = TRUE)library(ashr)
source("../code/ecdfz.R")
res = list()
for (i in 1:m) {
z = zmat[i, ]
p = (1 - pnorm(abs(z))) * 2
bh.fd = sum(p.adjust(p, method = "BH") <= 0.05)
pihat0.ash = get_pi0(ash(z, 1, method = "fdr"))
ecdfz.fit = ecdfz.optimal(z)
res[[i]] = list(z = z, p = p, bh.fd = bh.fd, pihat0.ash = pihat0.ash, ecdfz.fit = ecdfz.fit)
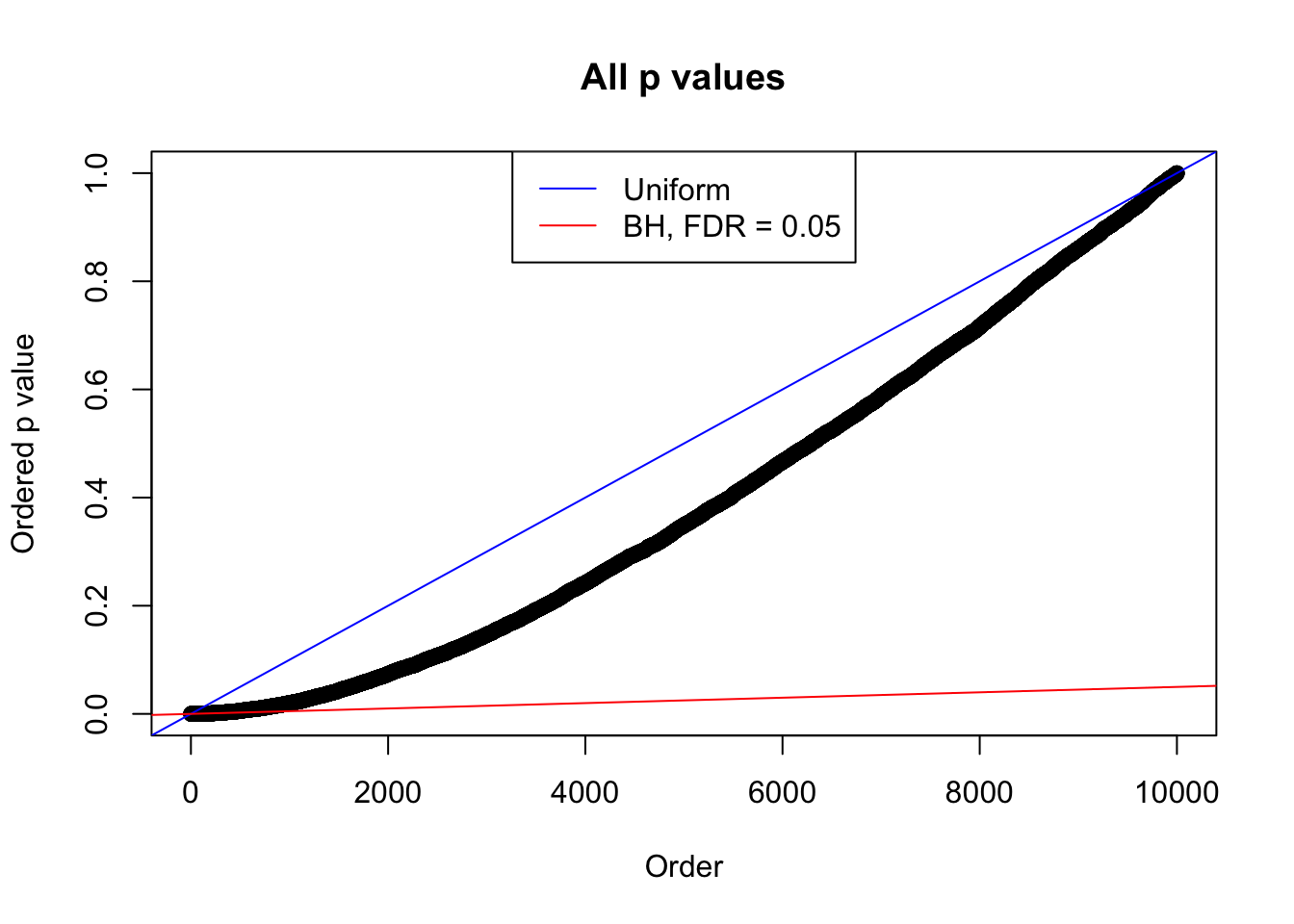
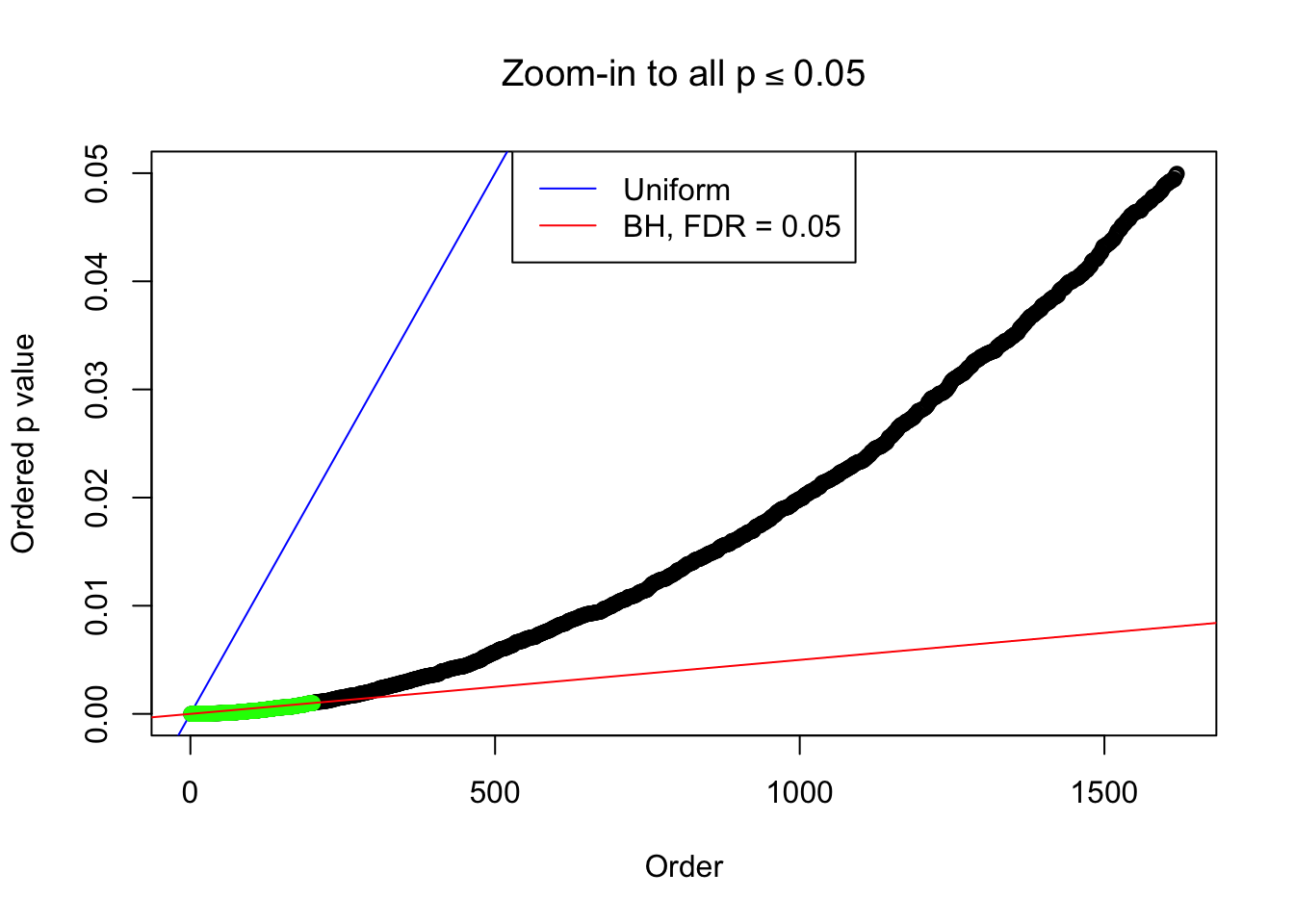
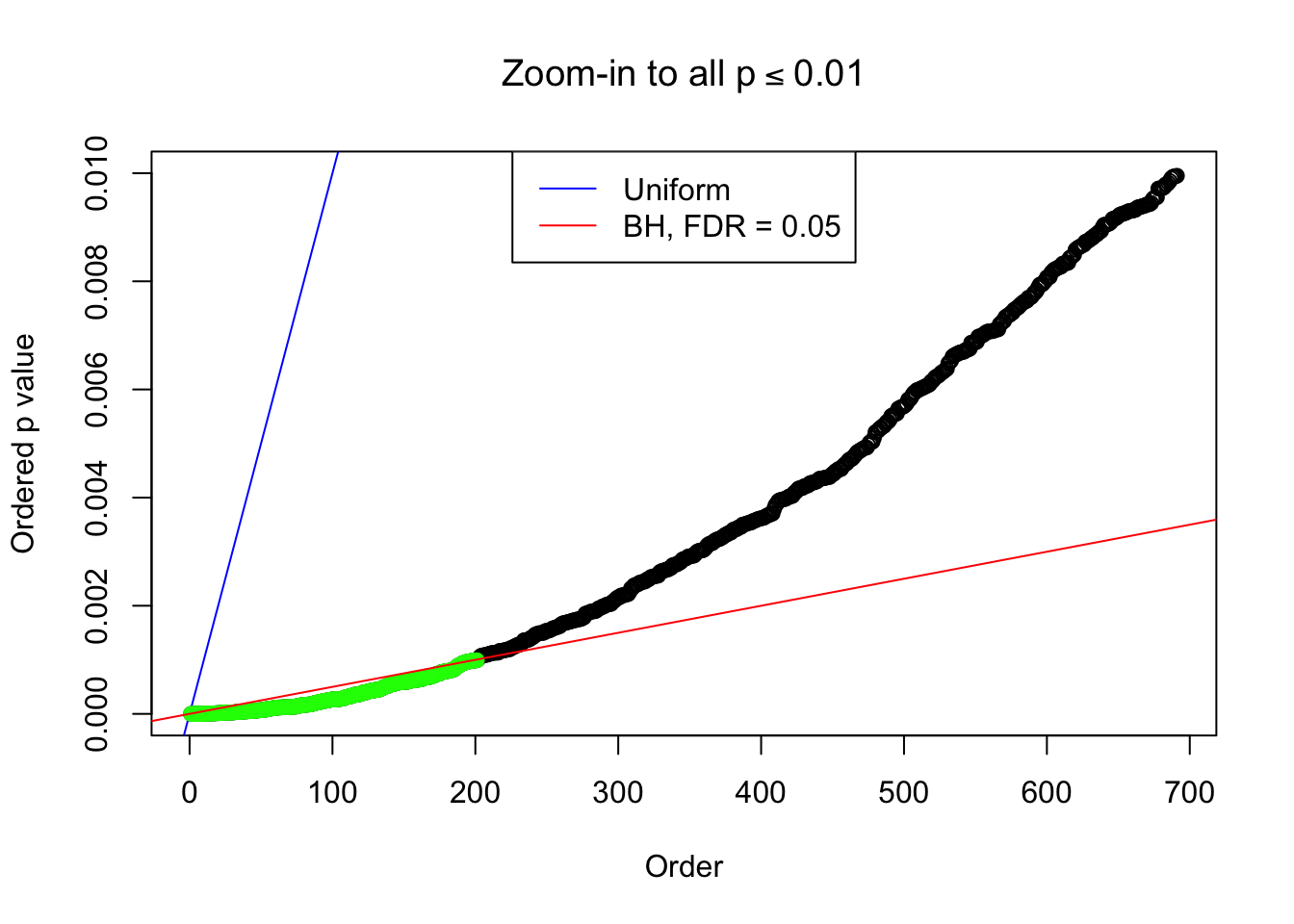
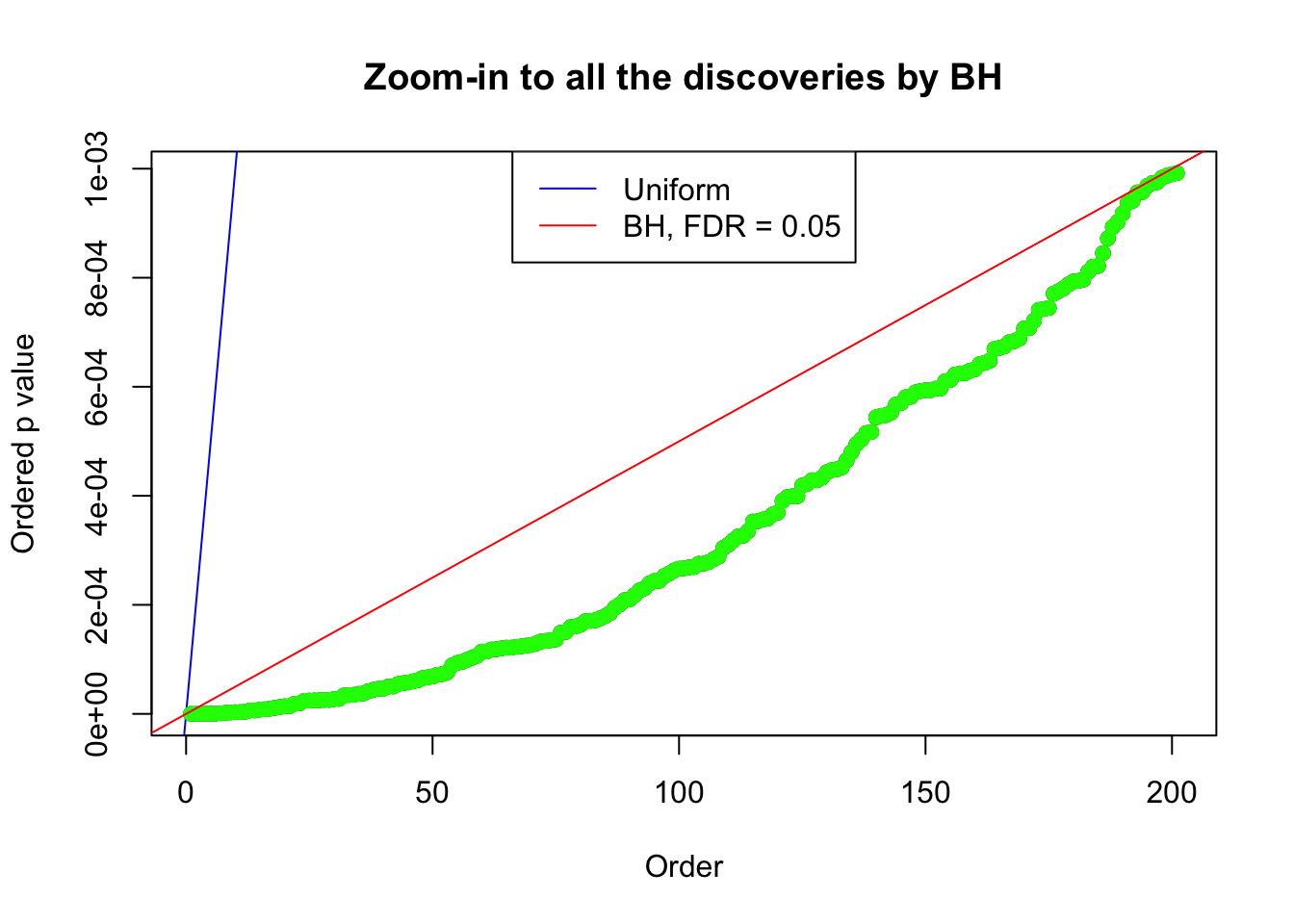
}Example 1 : Number of Discoveries: 246 ; pihat0 = 0.3245191
Log-likelihood with N(0, 2): -17704.62
Log-likelihood with Gaussian Derivatives: -17702.15
Log-likelihood ratio between true N(0, 2) and fitted Gaussian derivatives: -2.473037
Normalized weights:
1 : -0.0126888368547959 ; 2 : 0.717062378249889 ; 3 : -0.0184536200134752 ; 4 : 0.649465525394262 ; 5 : 0.00859163522314002 ; 6 : 0.521325079359314 ; 7 : 0.0334885164431775 ; 8 : 0.22636494735755 ;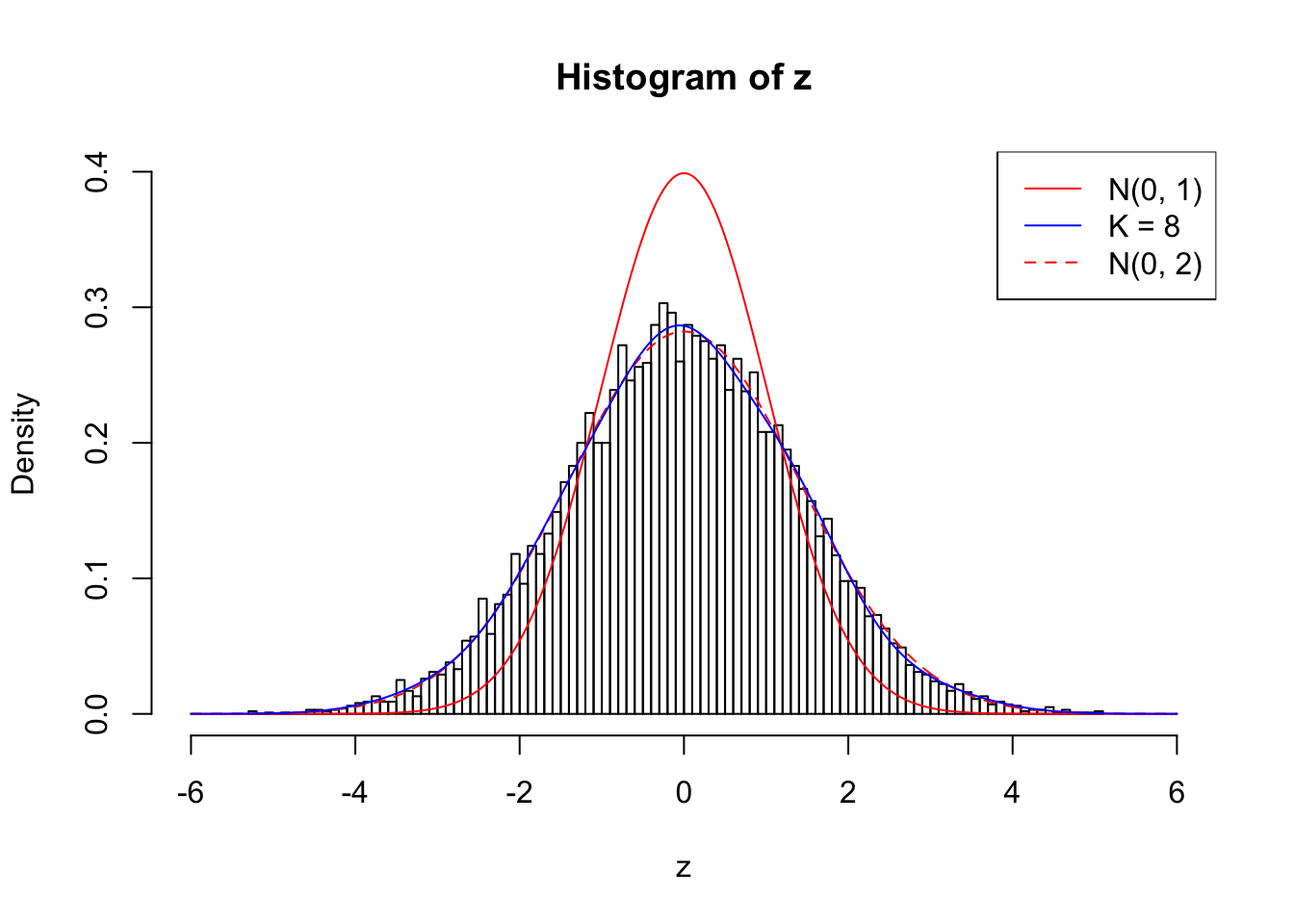
Zoom in to the left tail: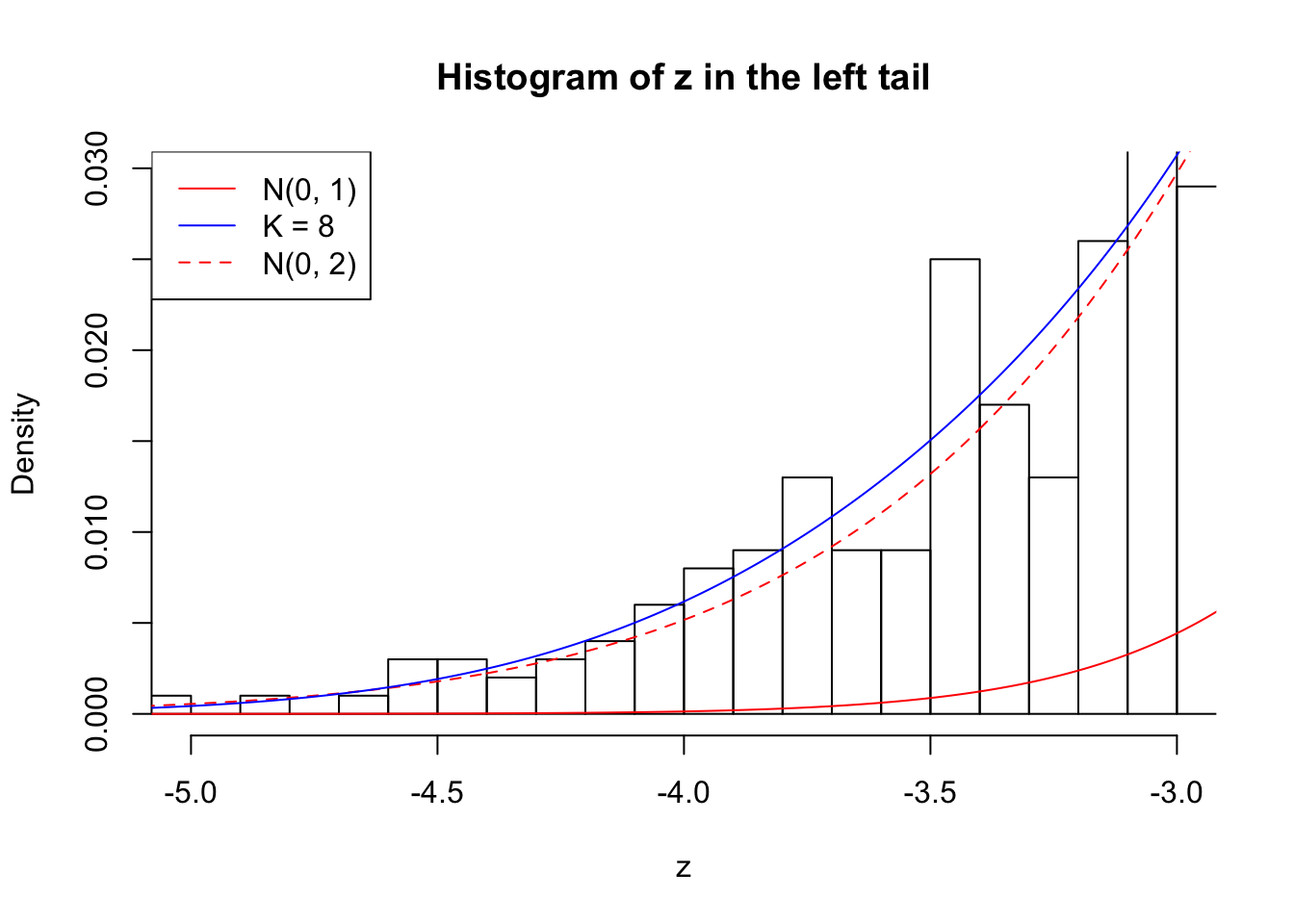
Zoom in to the right tail: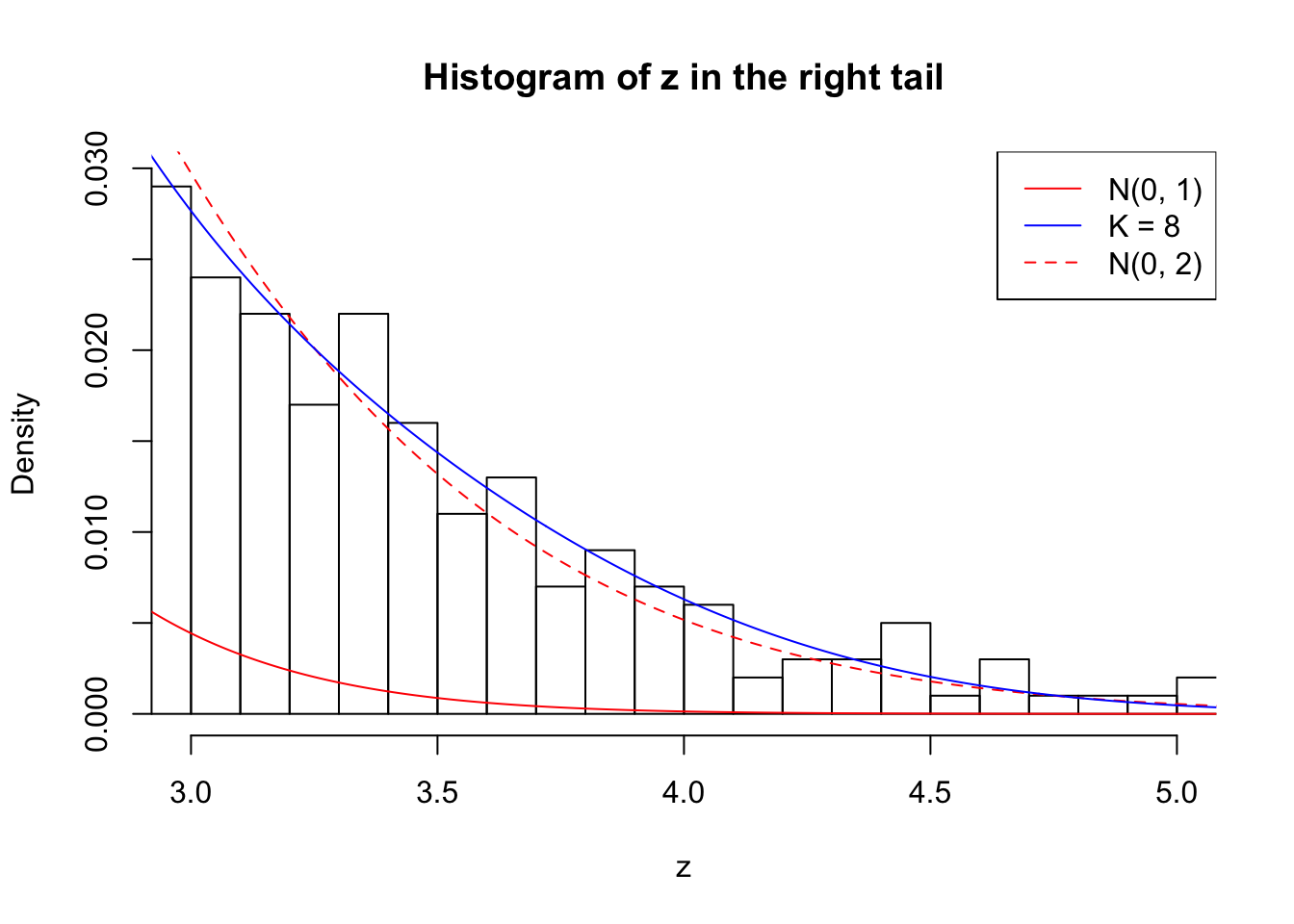
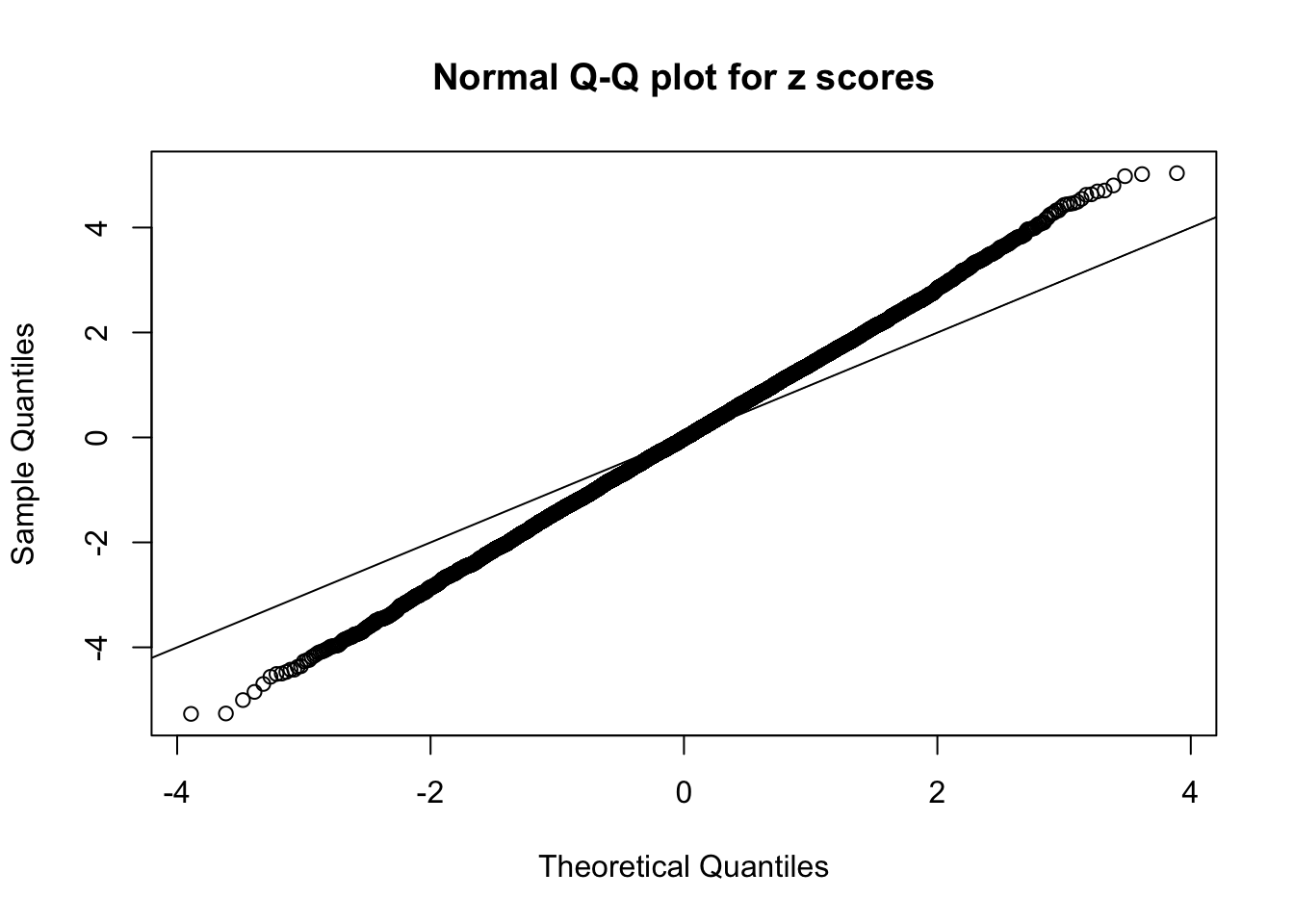
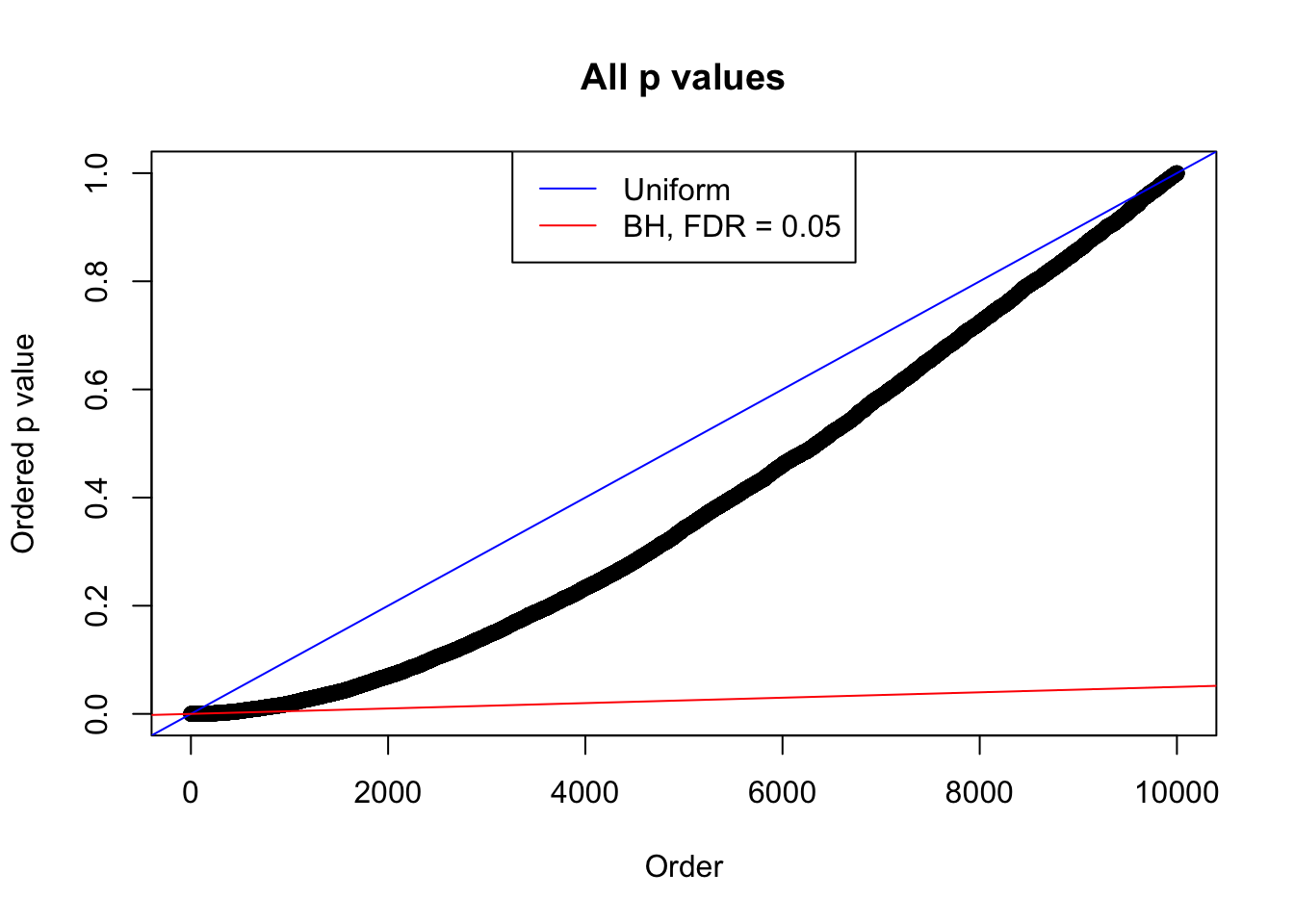
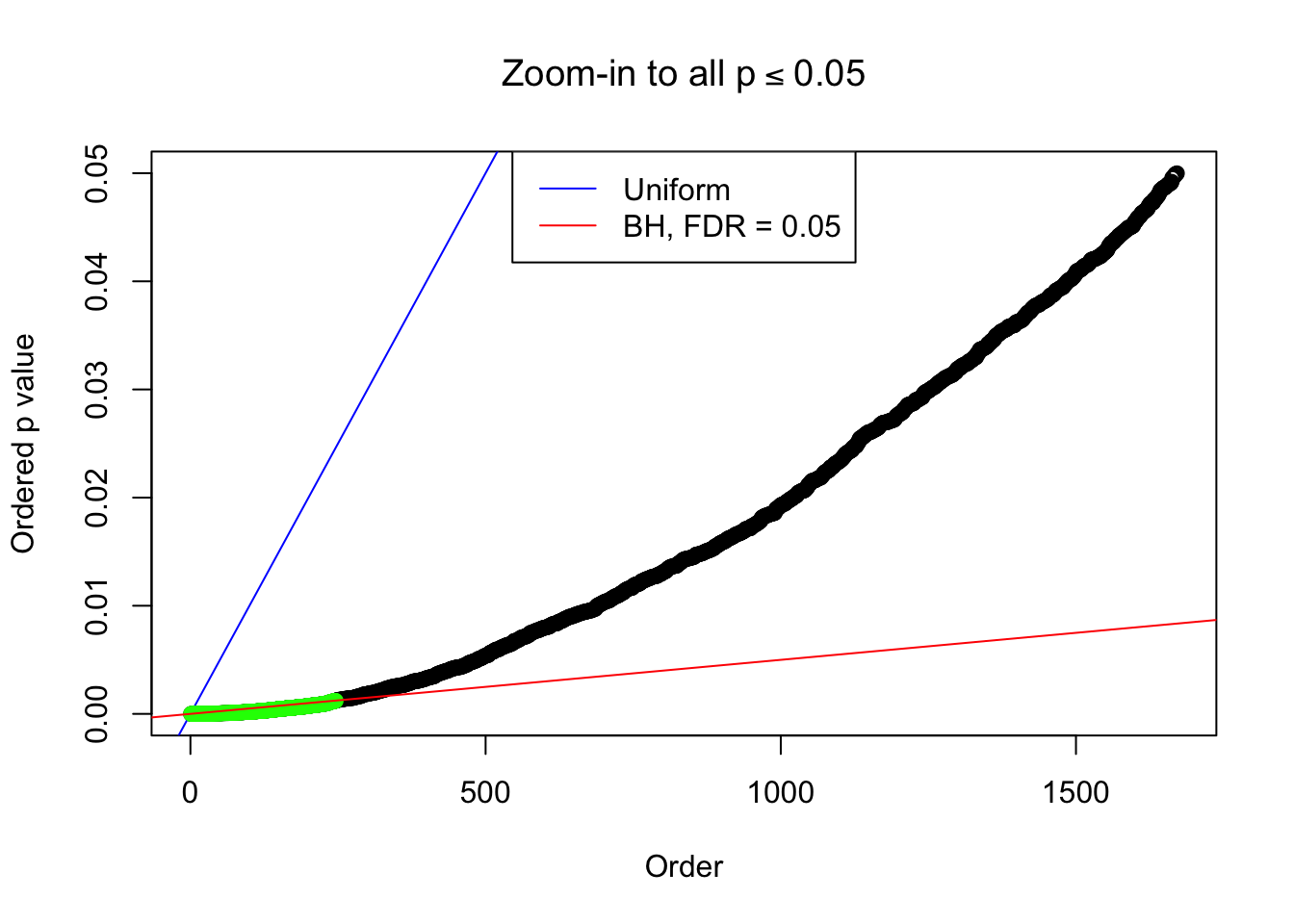
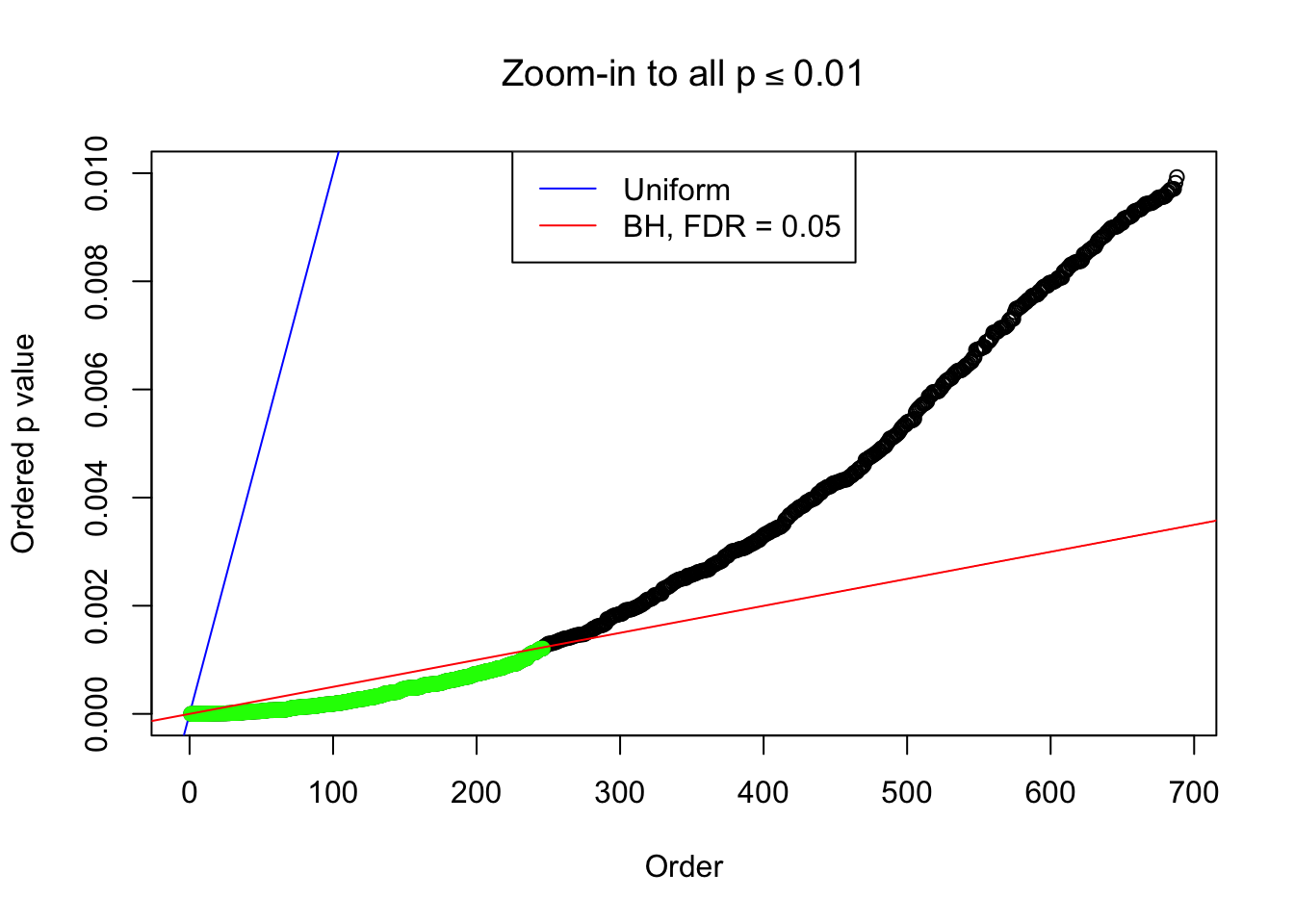
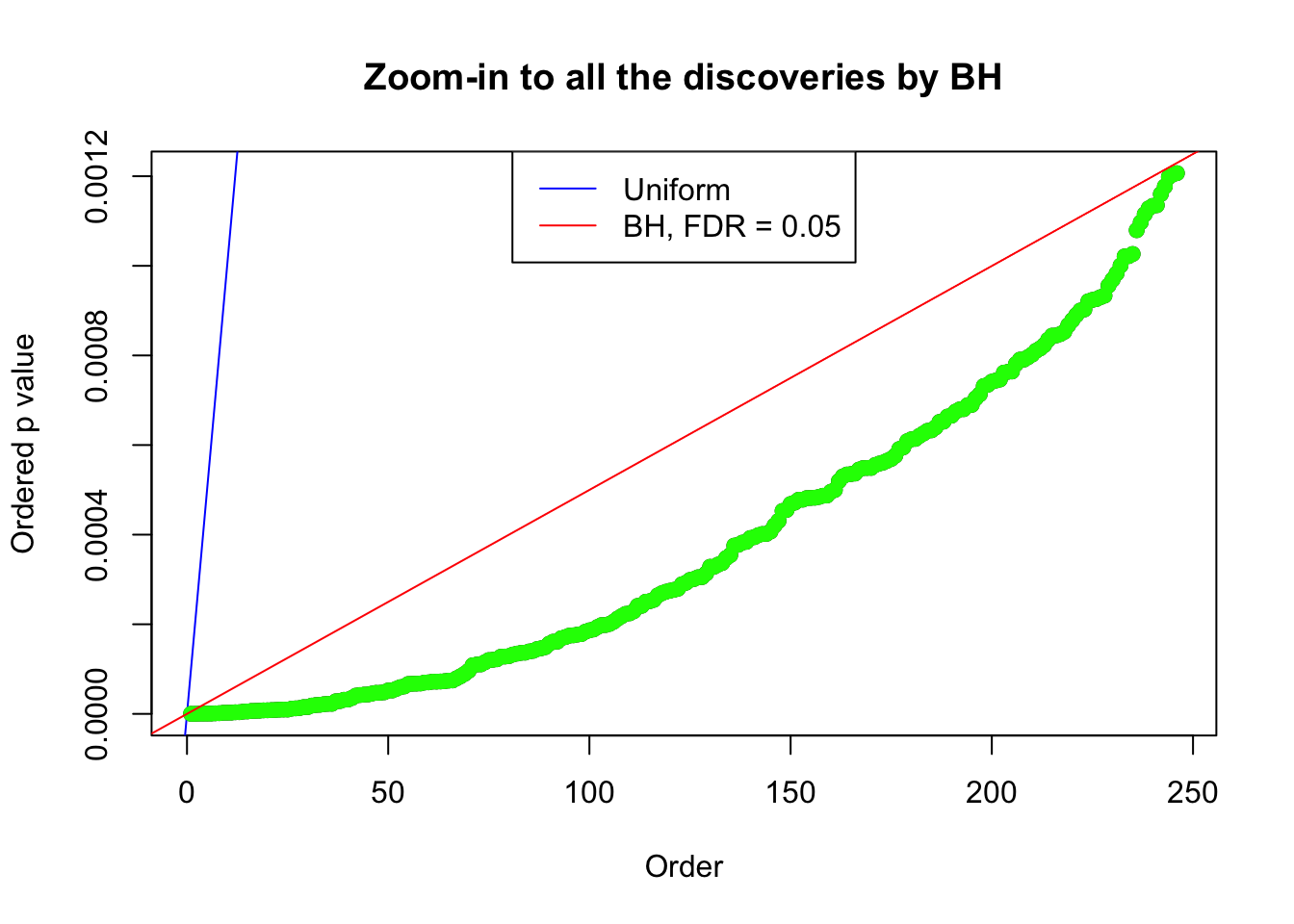
Example 2 : Number of Discoveries: 218 ; pihat0 = 0.3007316
Log-likelihood with N(0, 2): -17620.91
Log-likelihood with Gaussian Derivatives: -17618.13
Log-likelihood ratio between true N(0, 2) and fitted Gaussian derivatives: -2.787631
Normalized weights:
1 : 0.0102680011779709 ; 2 : 0.696012169853609 ; 3 : 0.0113000171720435 ; 4 : 0.544236663386519 ; 5 : -0.0208432030918437 ; 6 : 0.359654087688657 ; 7 : 0.00449356234470338 ; 8 : 0.129368209367989 ;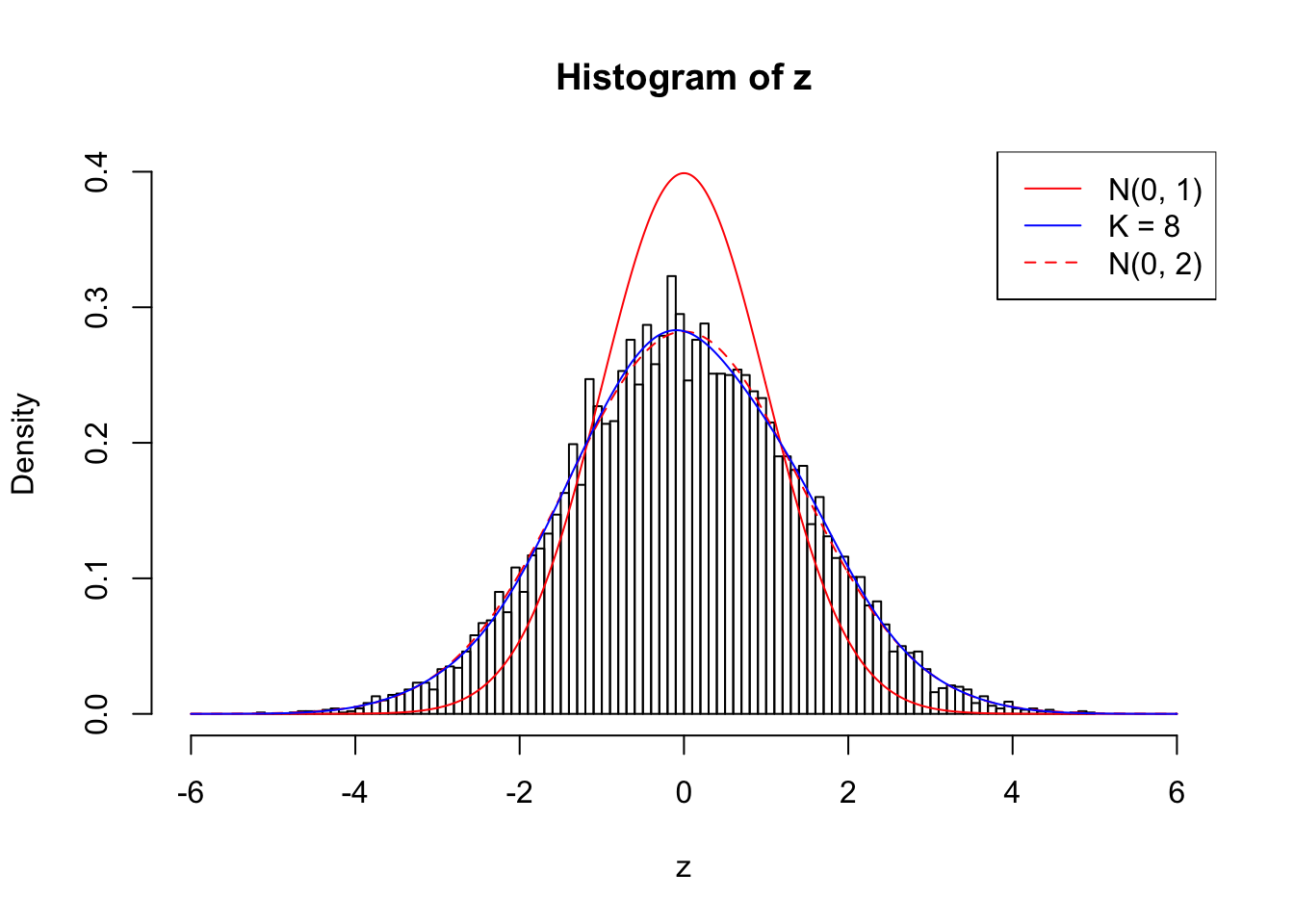
Zoom in to the left tail: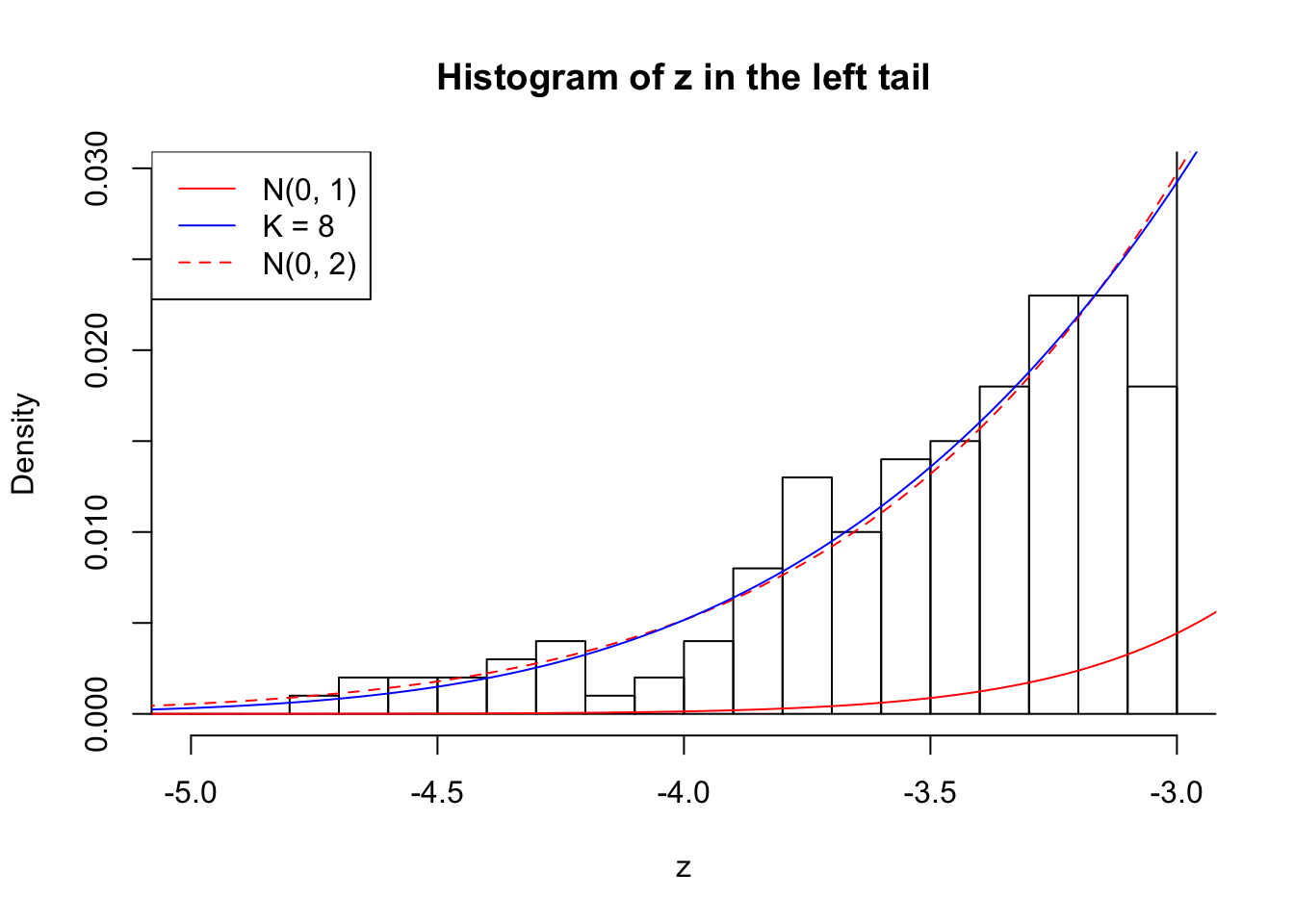
Zoom in to the right tail: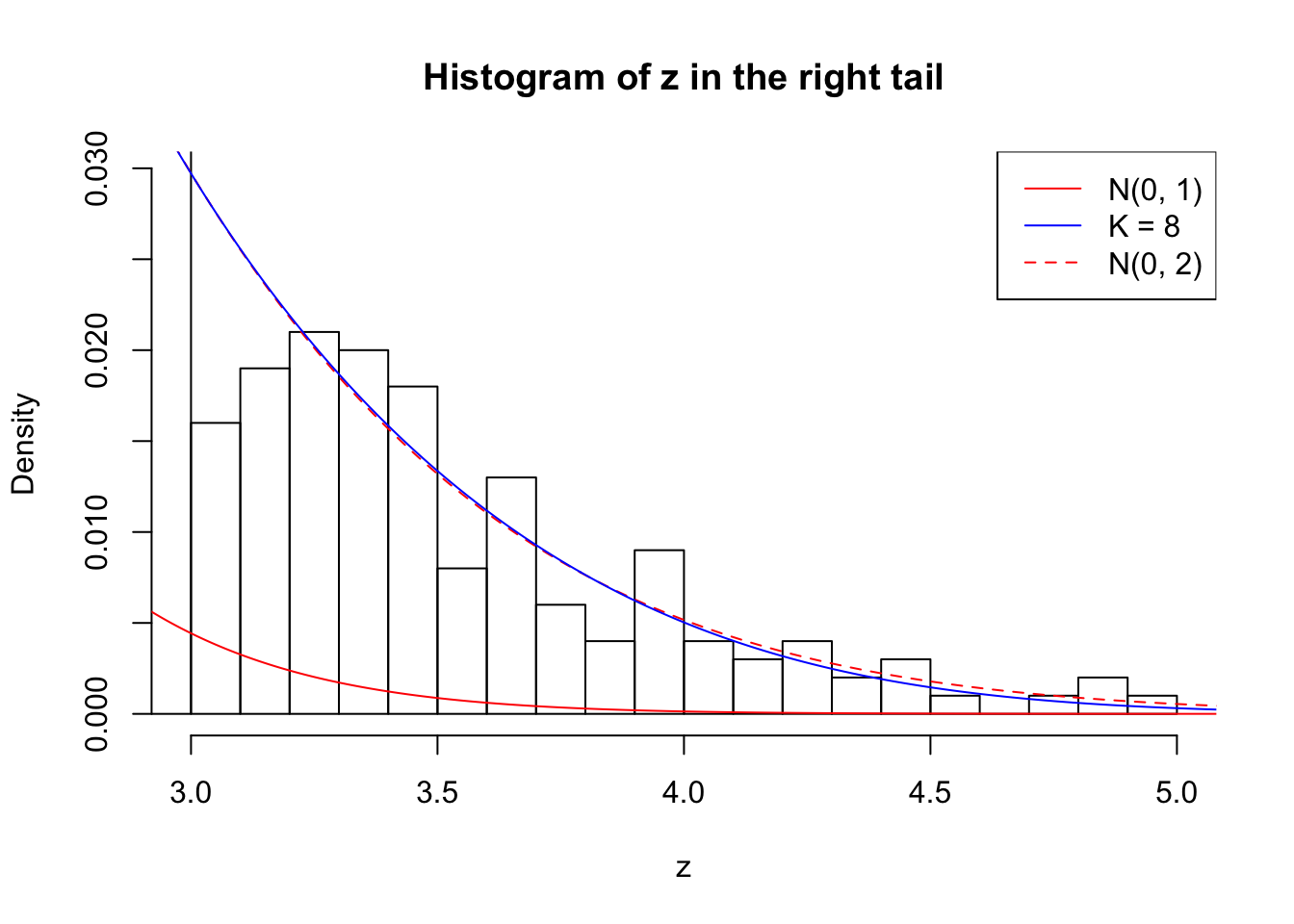
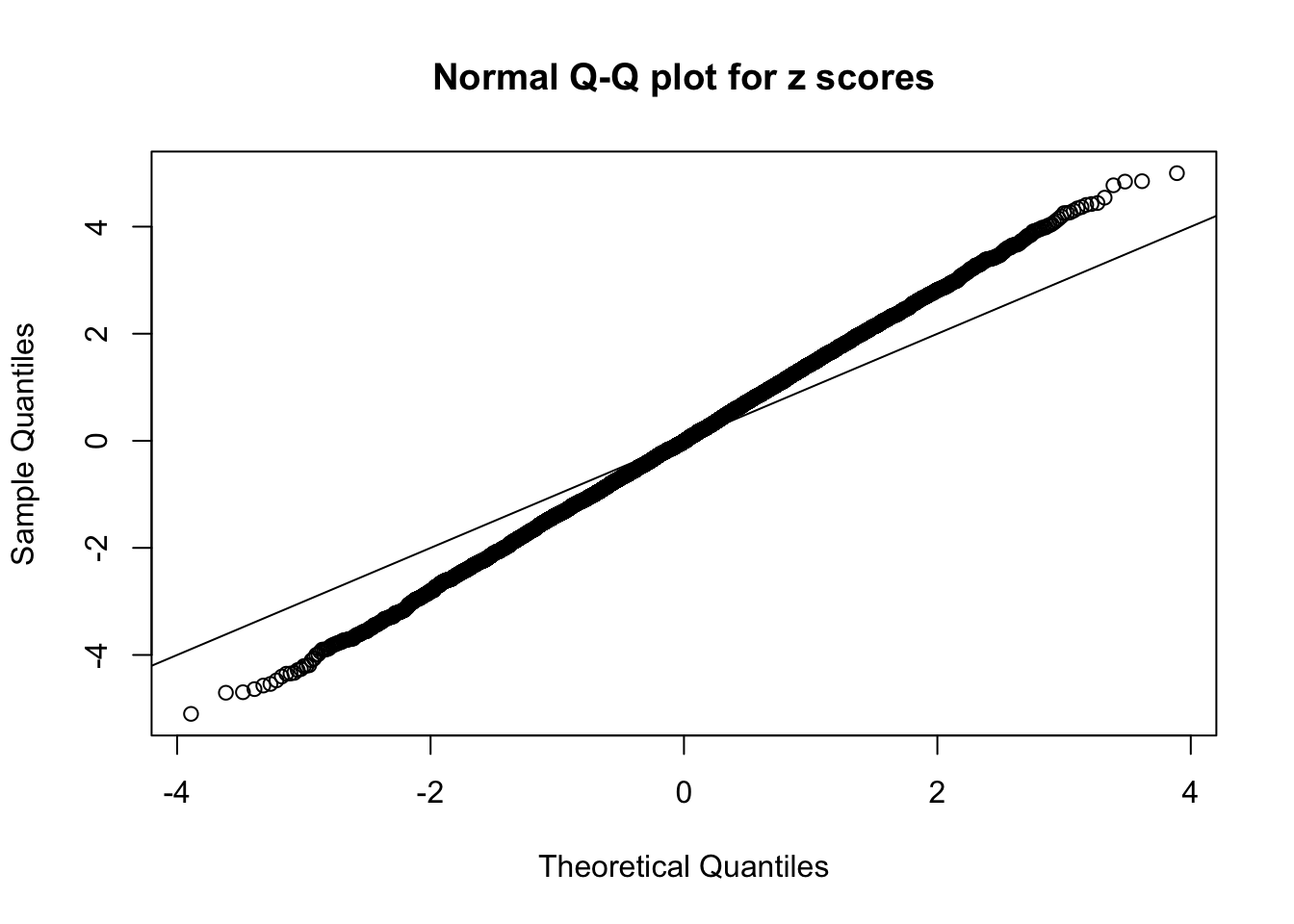
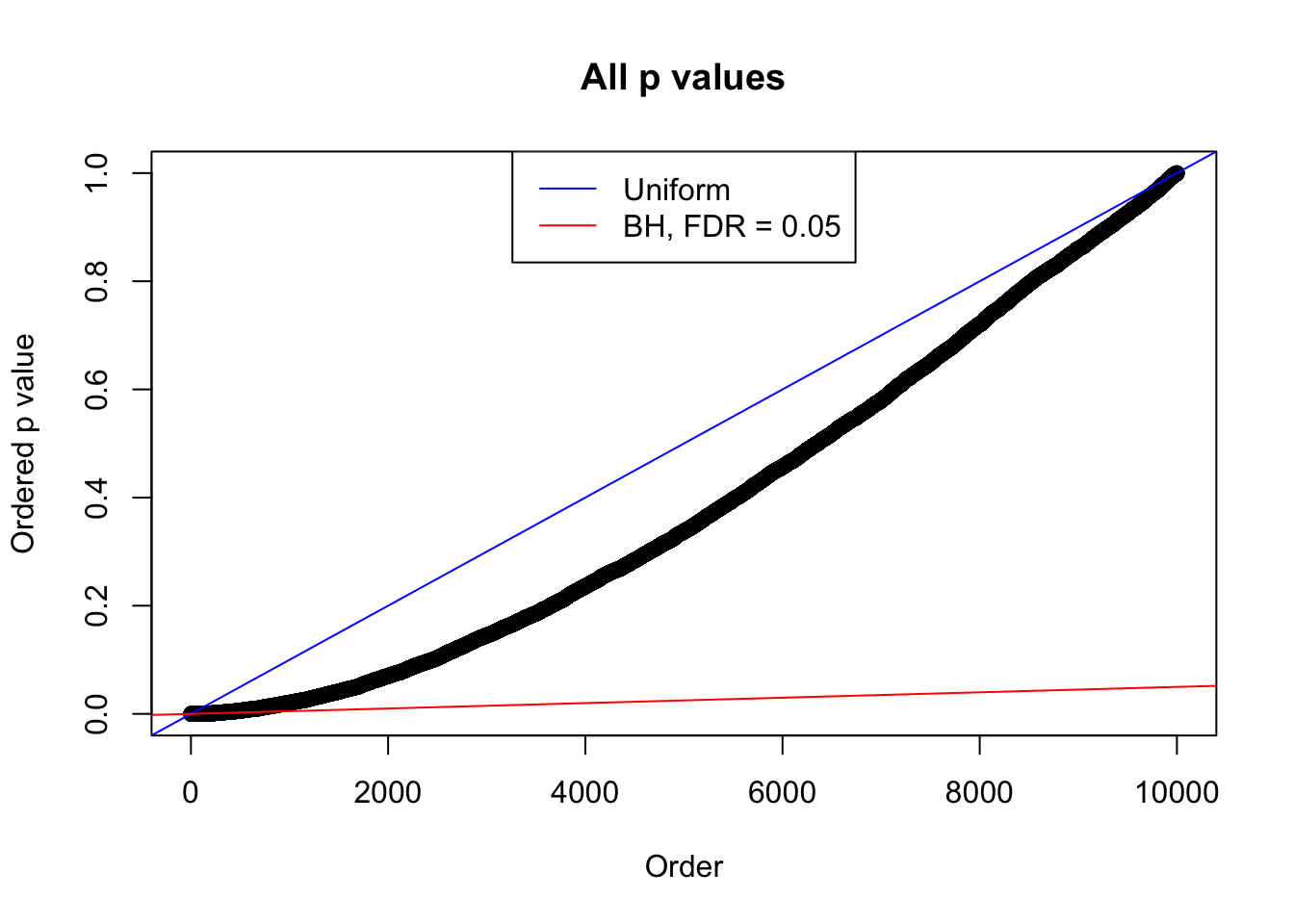
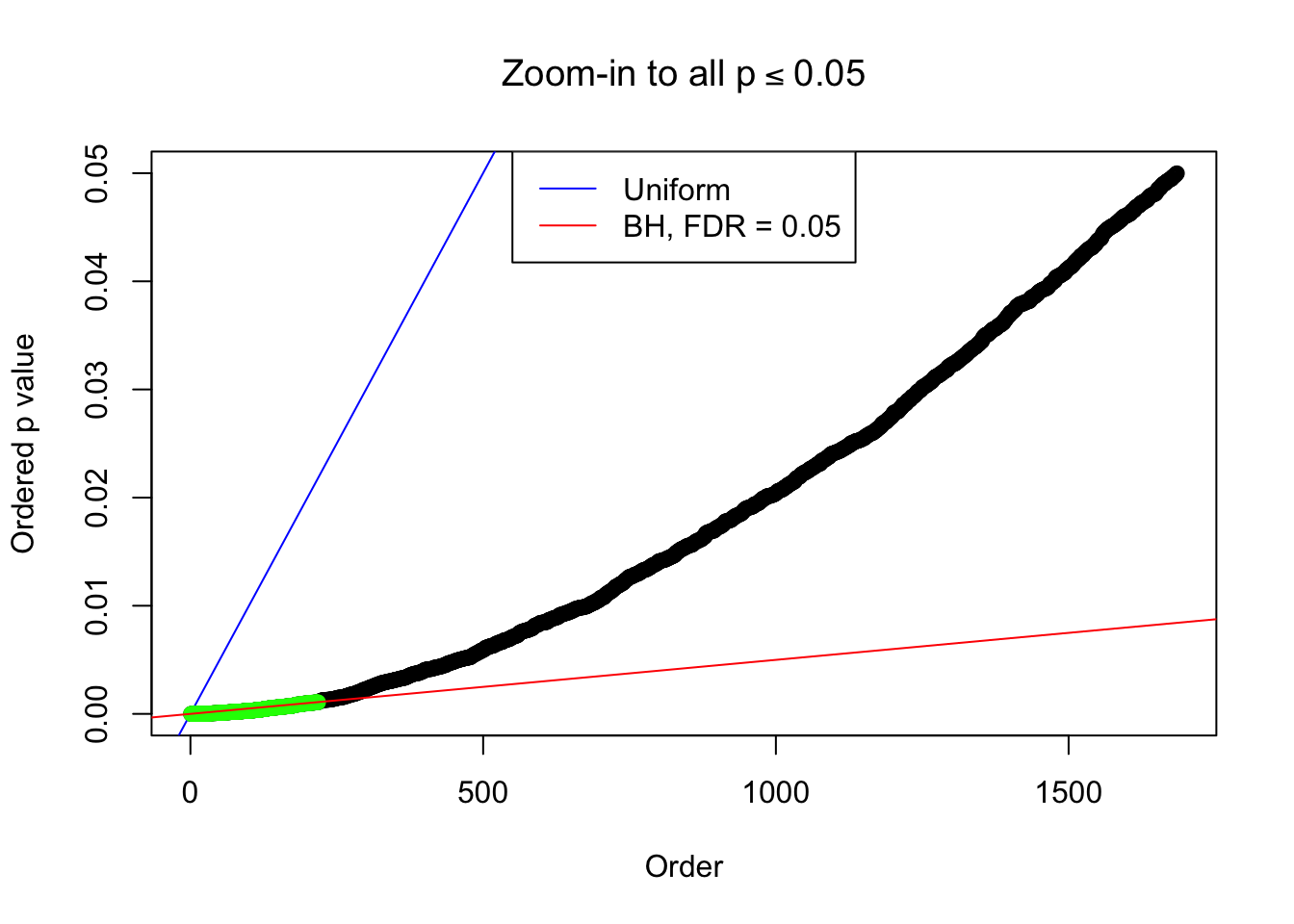
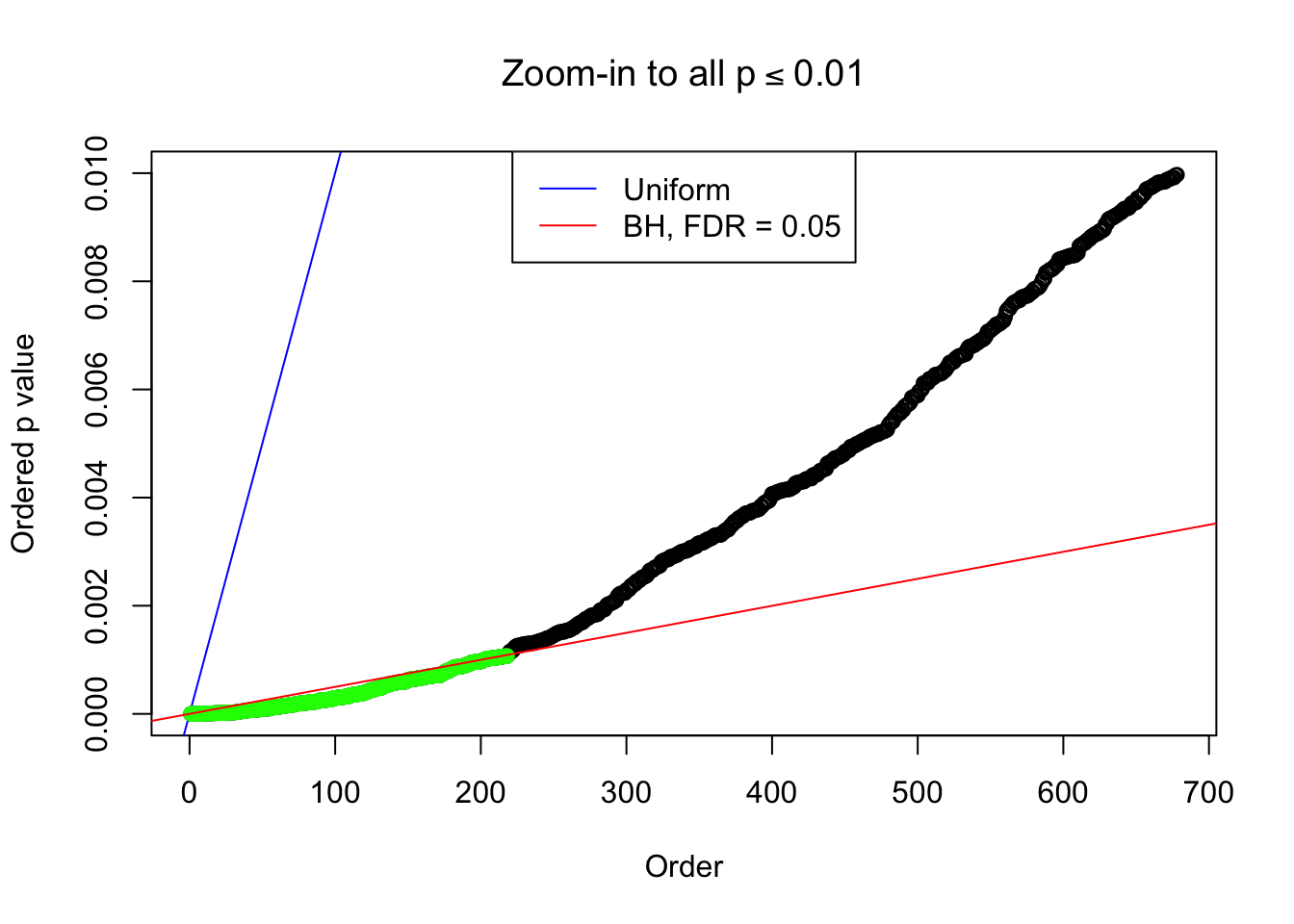
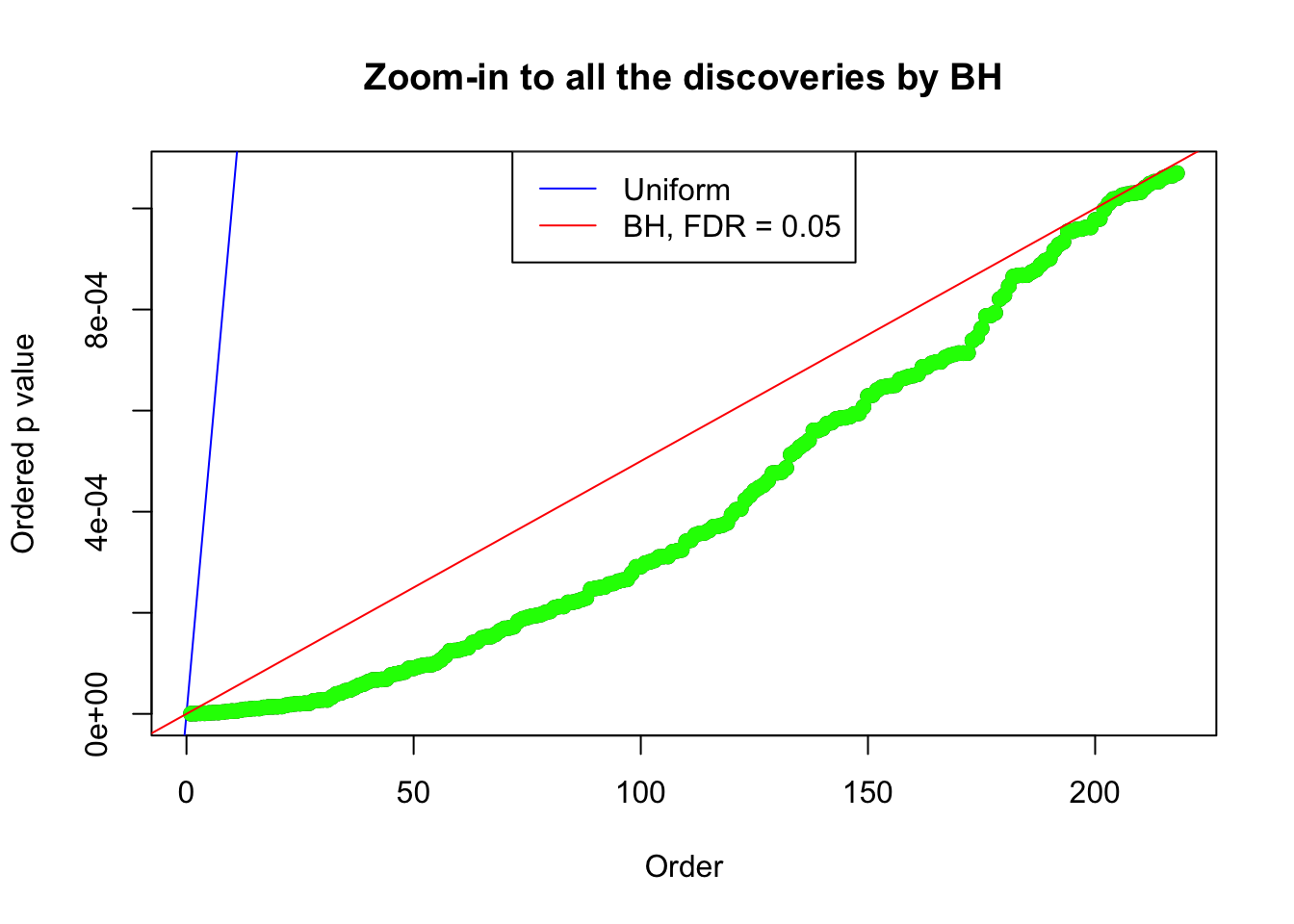
Example 3 : Number of Discoveries: 201 ; pihat0 = 0.3524008
Log-likelihood with N(0, 2): -17627.66
Log-likelihood with Gaussian Derivatives: -17623.26
Log-likelihood ratio between true N(0, 2) and fitted Gaussian derivatives: -4.397359
Normalized weights:
1 : 0.000611199281683122 ; 2 : 0.697833563596919 ; 3 : -9.24232505276873e-05 ; 4 : 0.593310577011007 ; 5 : 0.0690423192366928 ; 6 : 0.402719962212205 ; 7 : 0.0821756084741036 ; 8 : 0.137136244590824 ;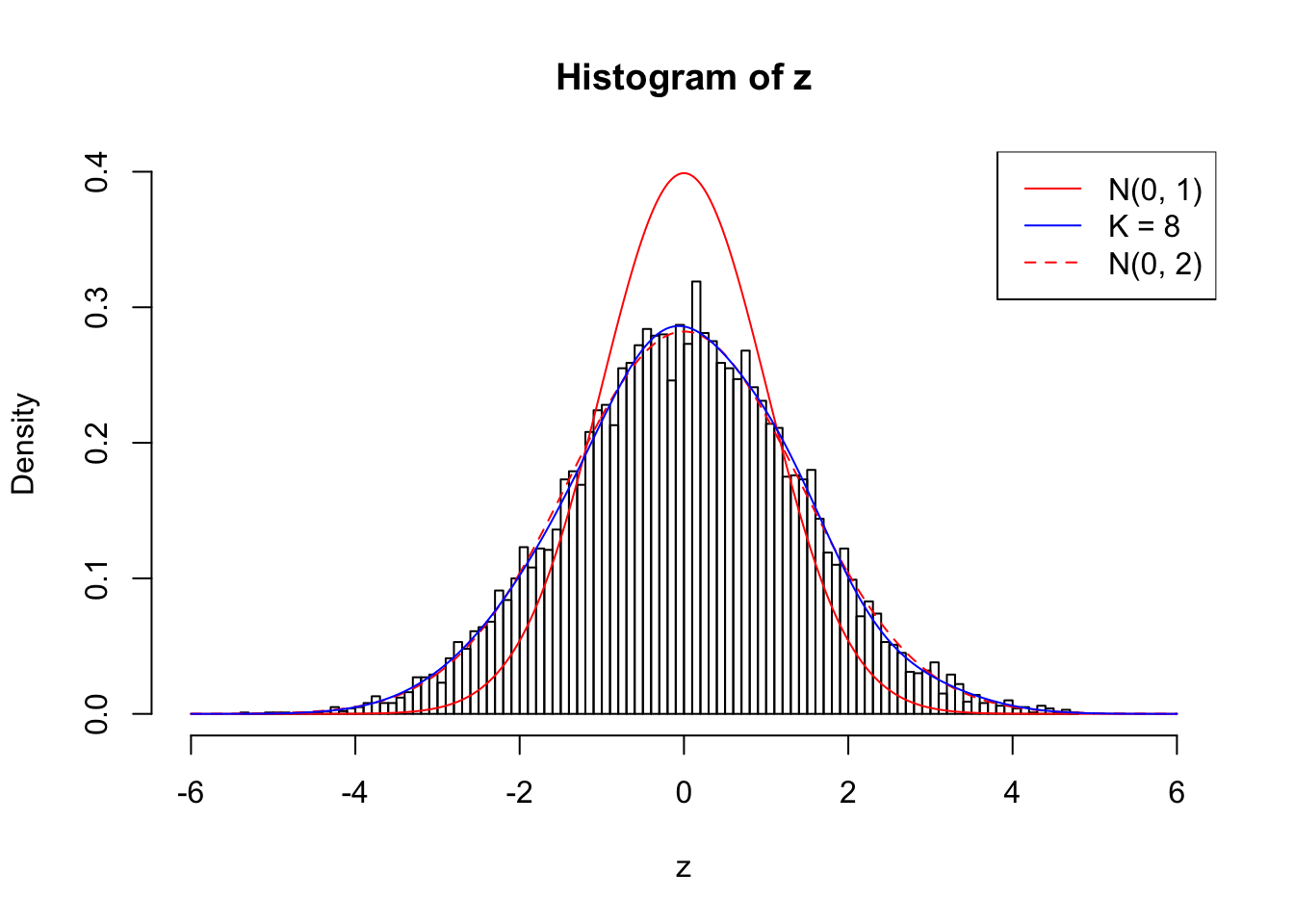
Zoom in to the left tail: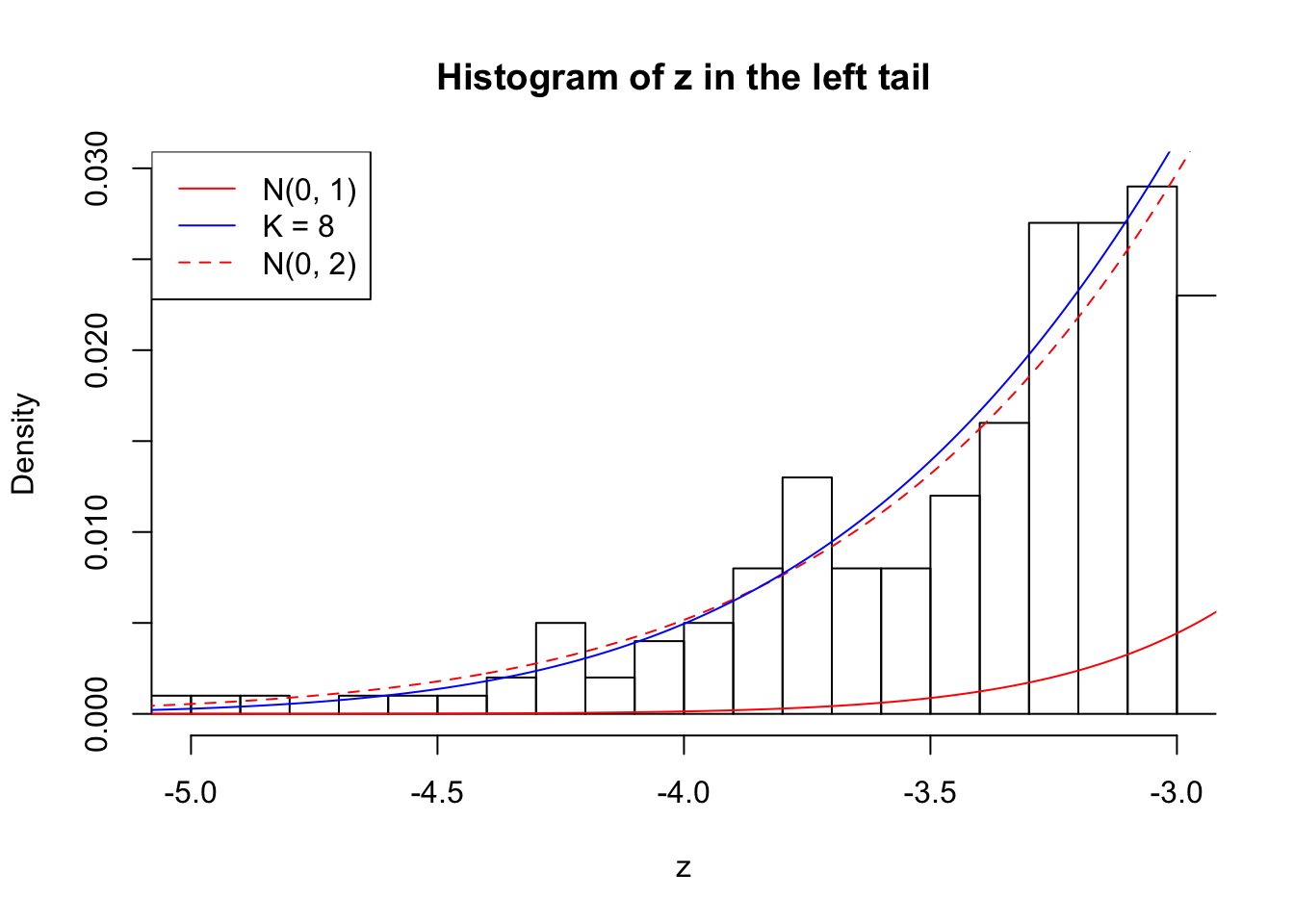
Zoom in to the right tail: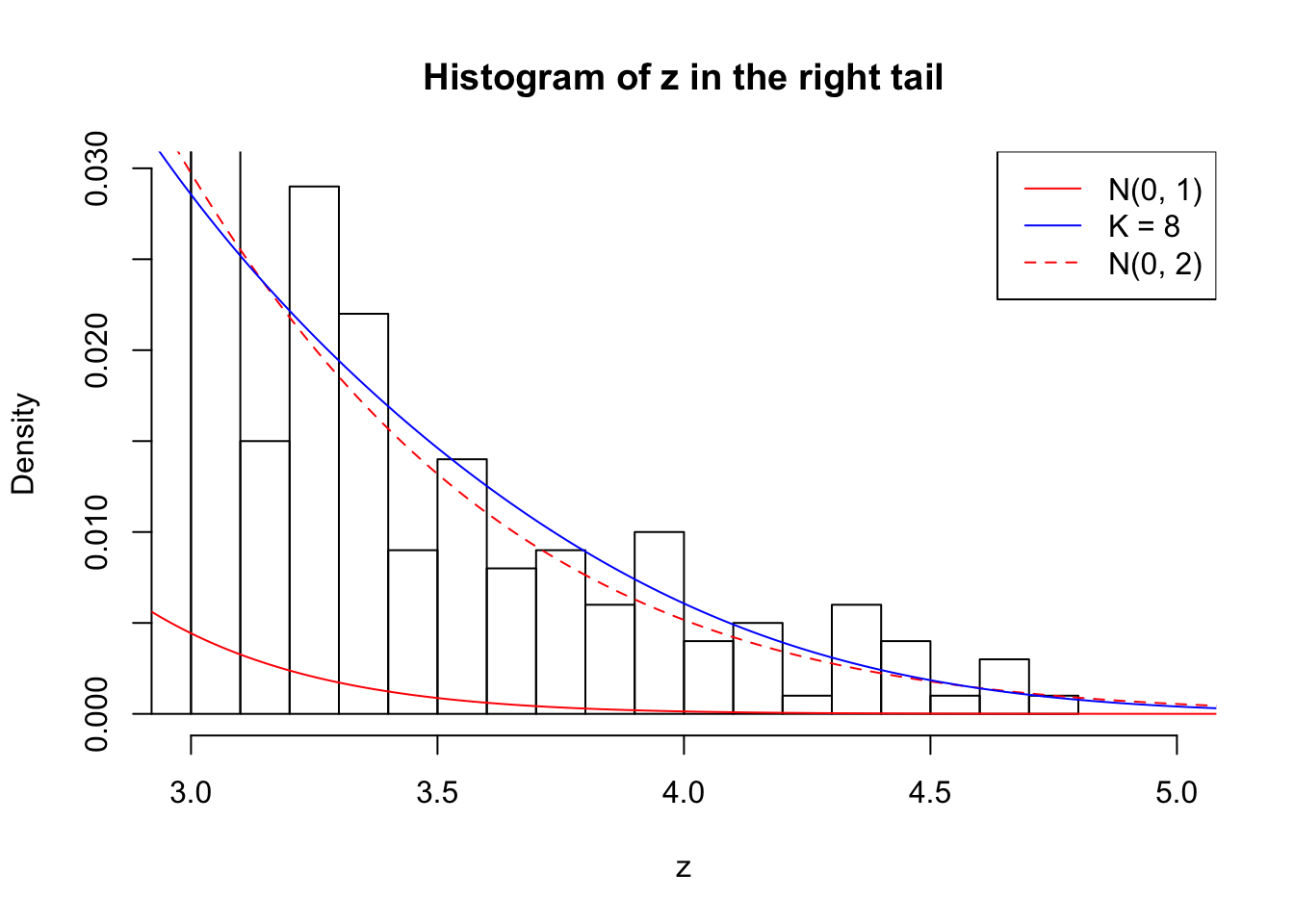
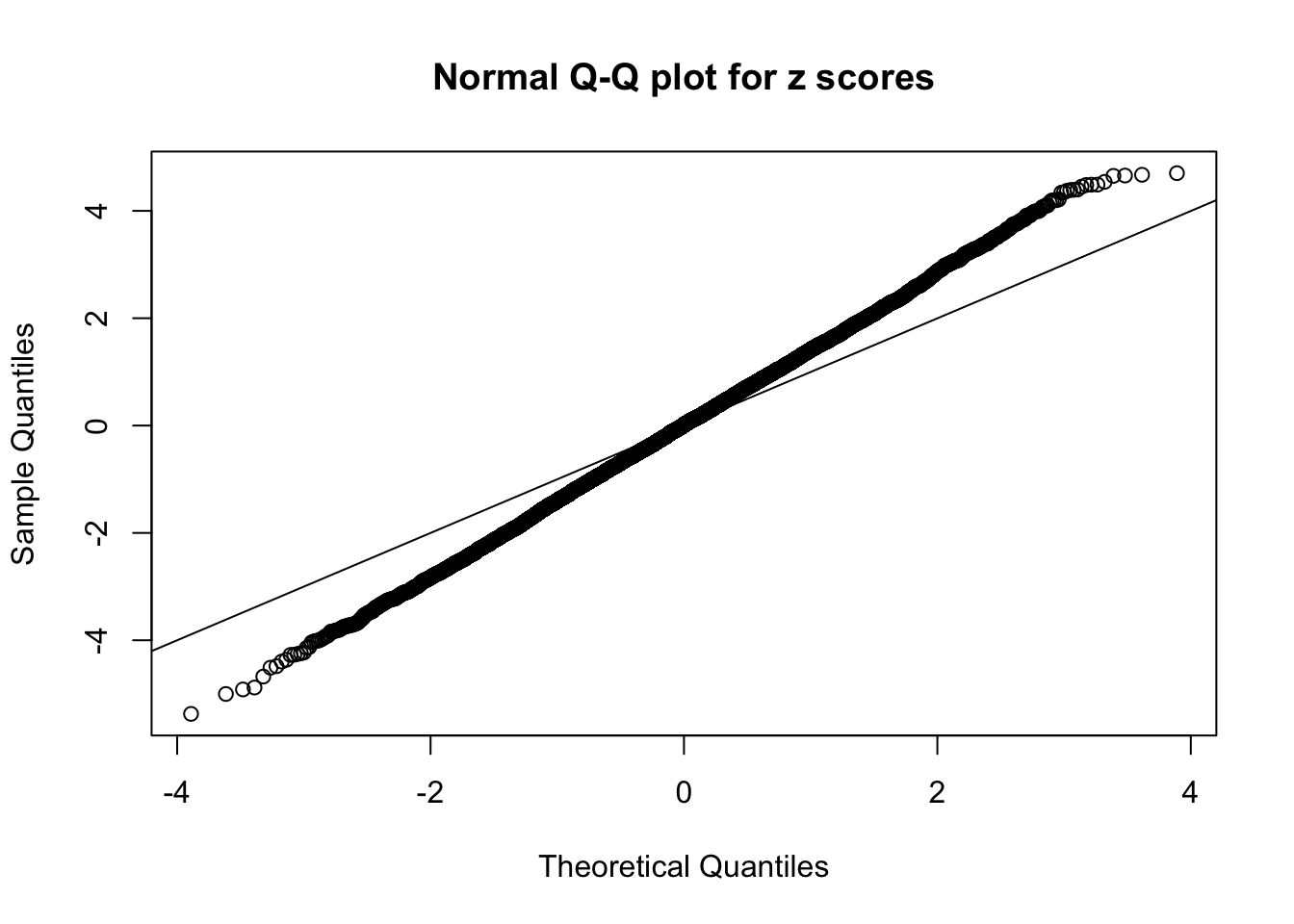
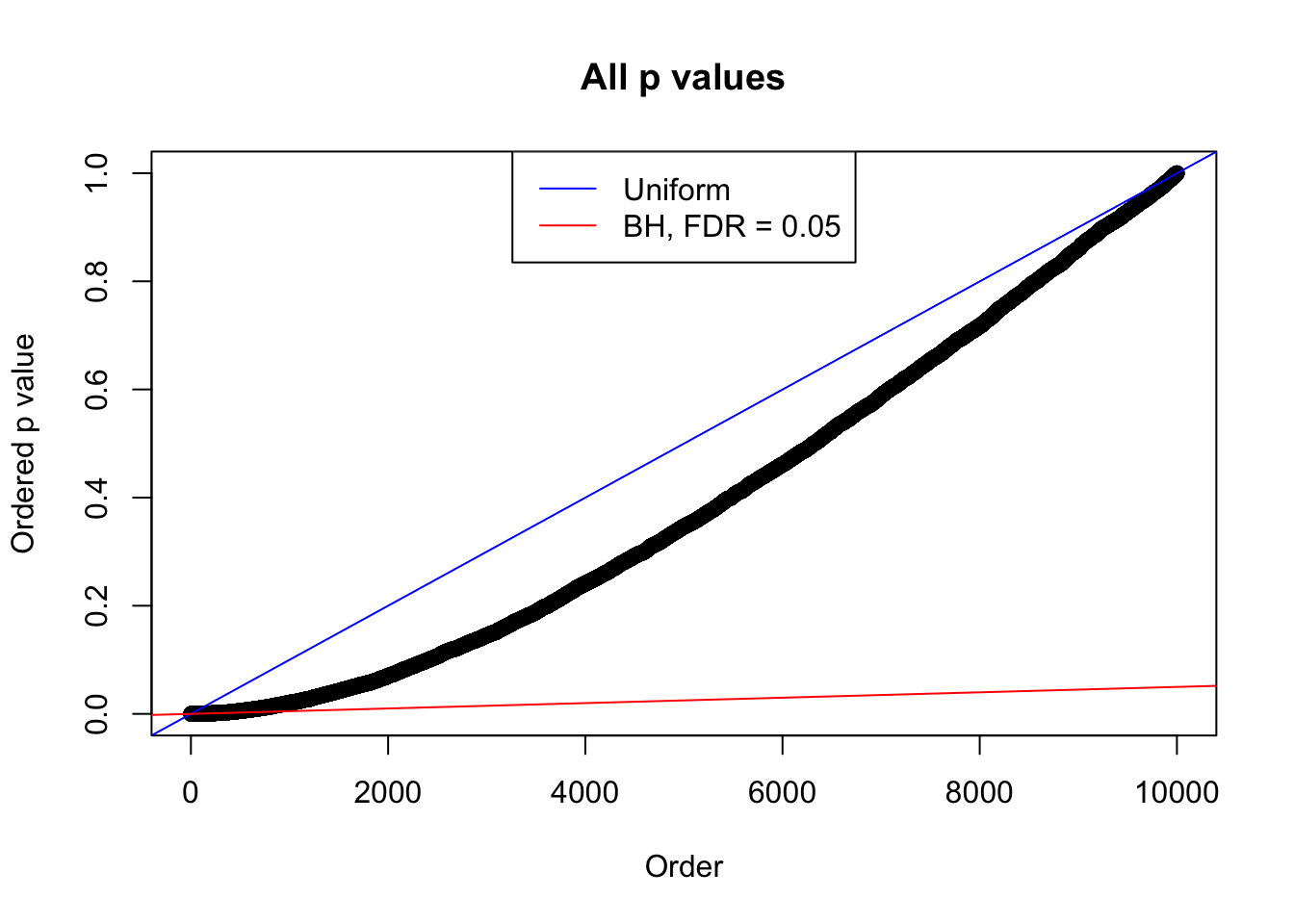
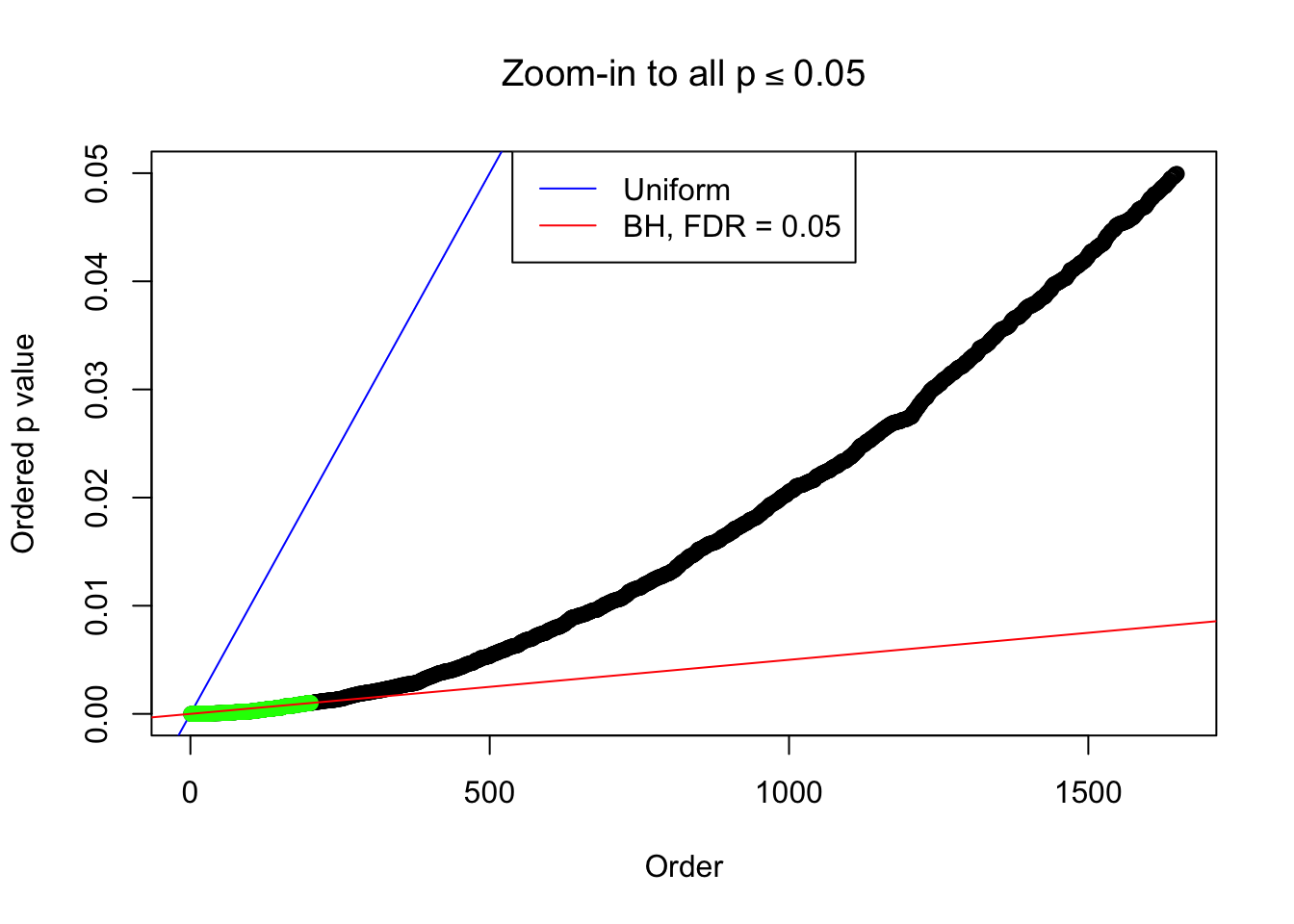
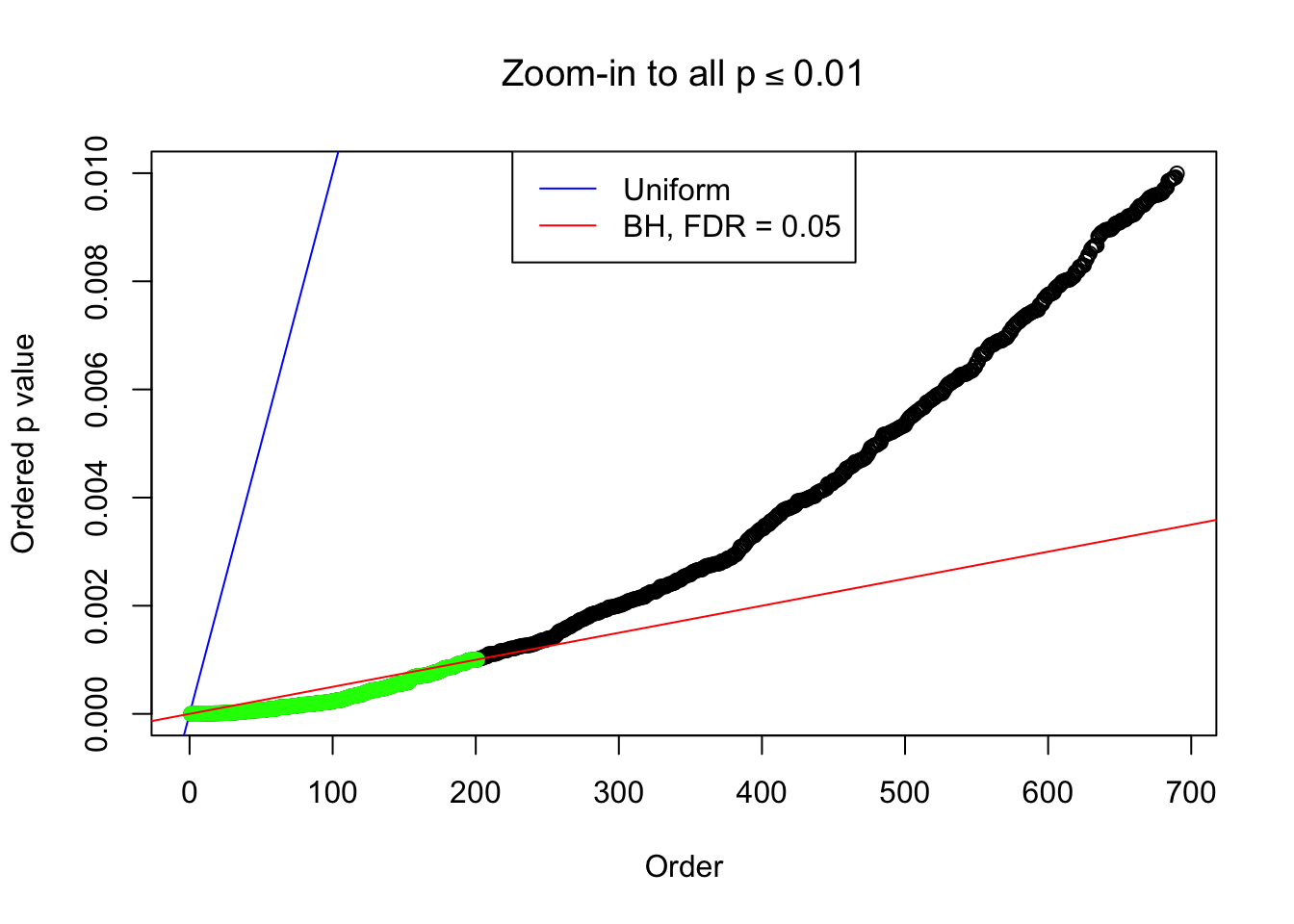
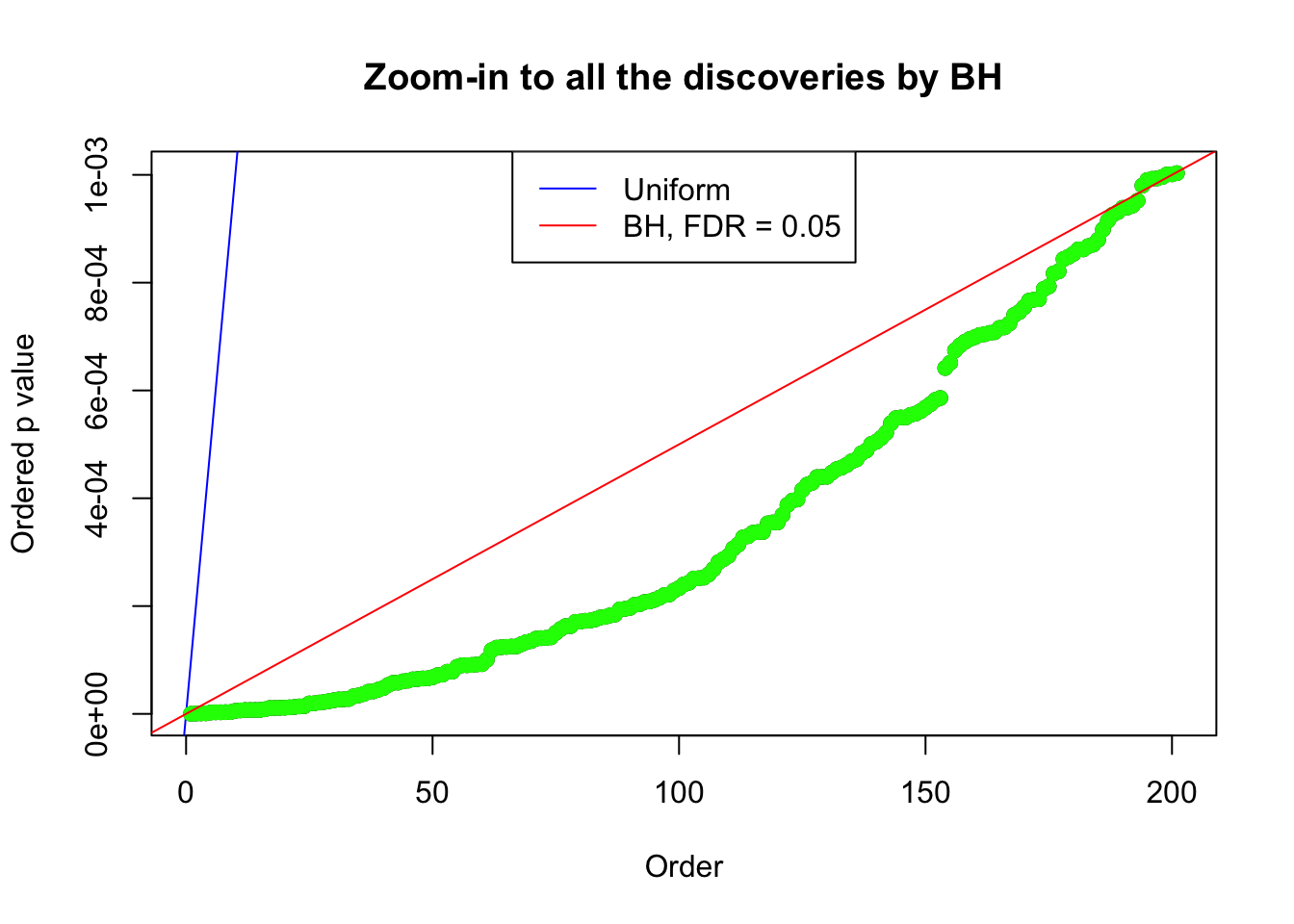
Example 4 : Number of Discoveries: 134 ; pihat0 = 0.3039997
Log-likelihood with N(0, 2): -17572.28
Log-likelihood with Gaussian Derivatives: -17589.35
Log-likelihood ratio between true N(0, 2) and fitted Gaussian derivatives: 17.07424
Normalized weights:
1 : -0.00303021567753385 ; 2 : 0.667140676046508 ; 3 : -0.00744442518950379 ; 4 : 0.4335954662891 ; 5 : 0.00652056989516479 ; 6 : 0.163579551221406 ; 7 : 0.0434395776822699 ;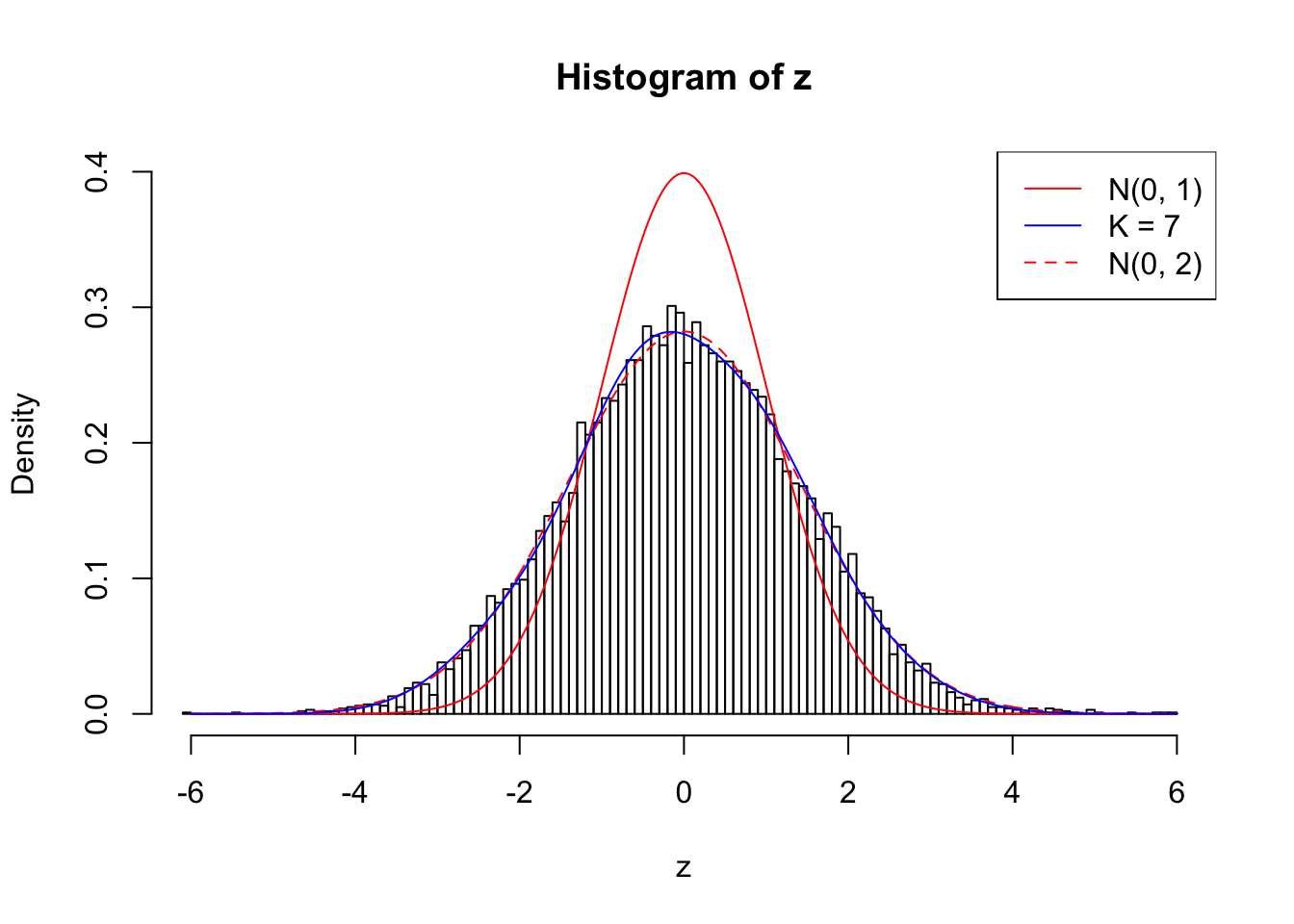
Zoom in to the left tail: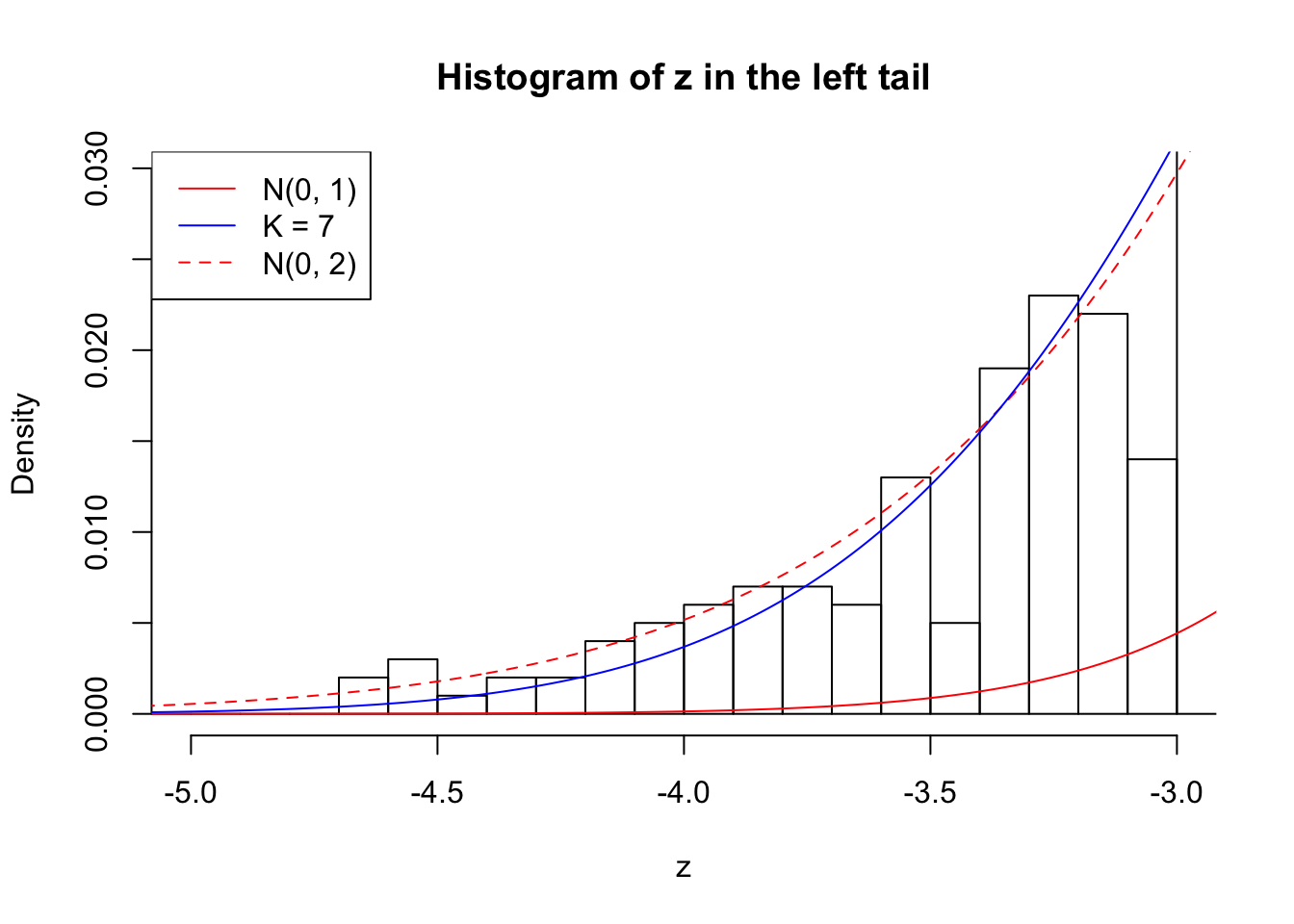
Zoom in to the right tail: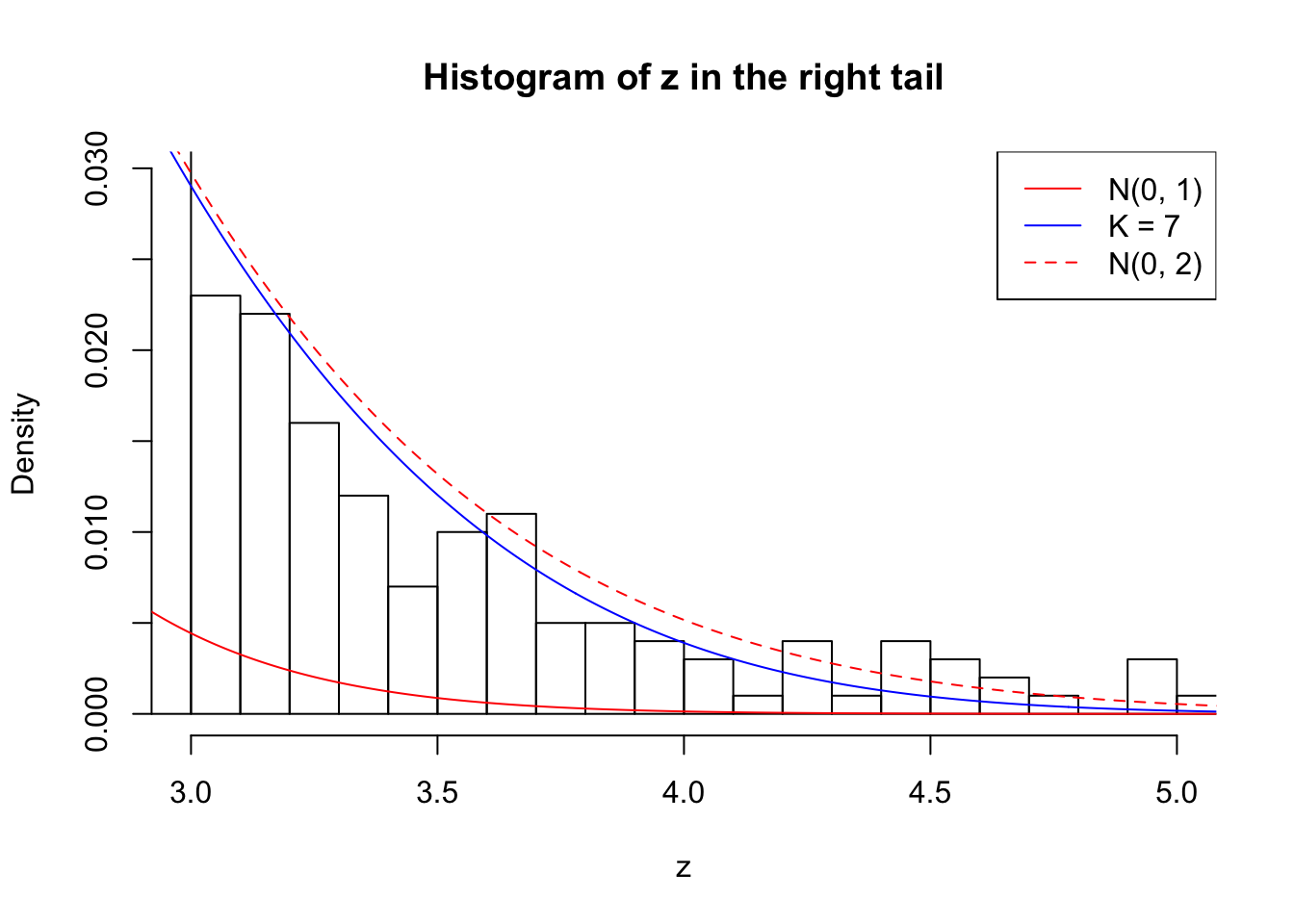
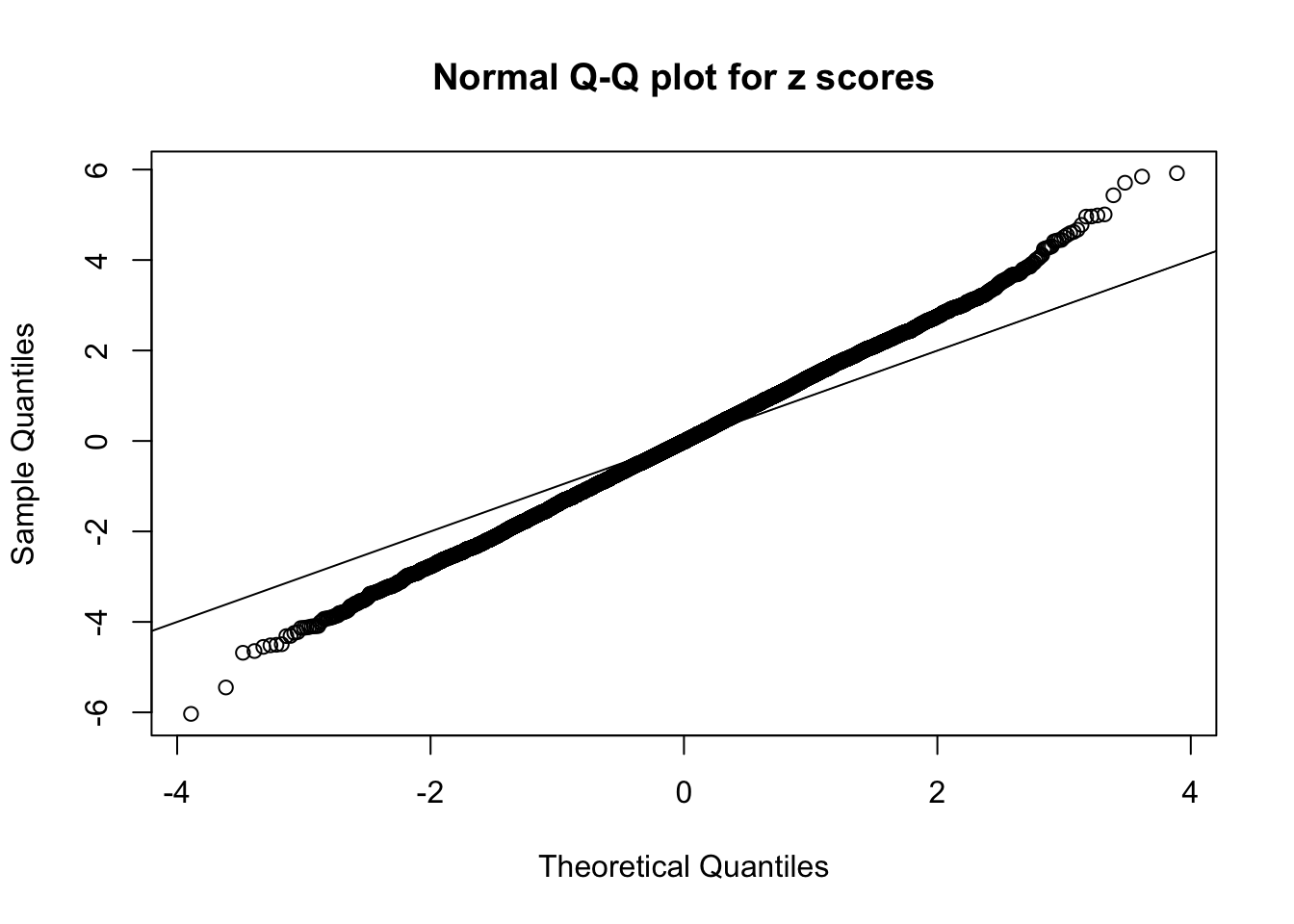
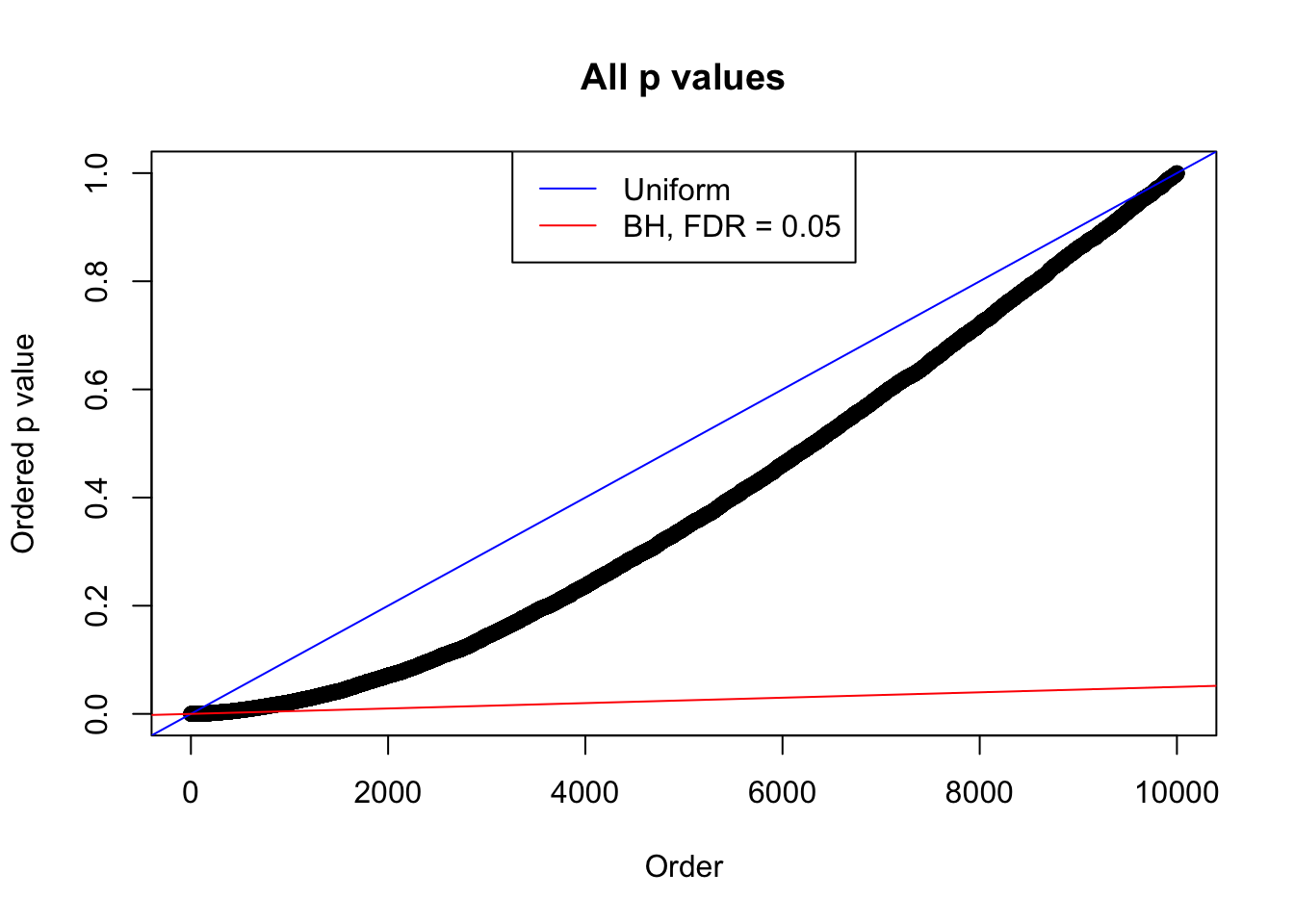
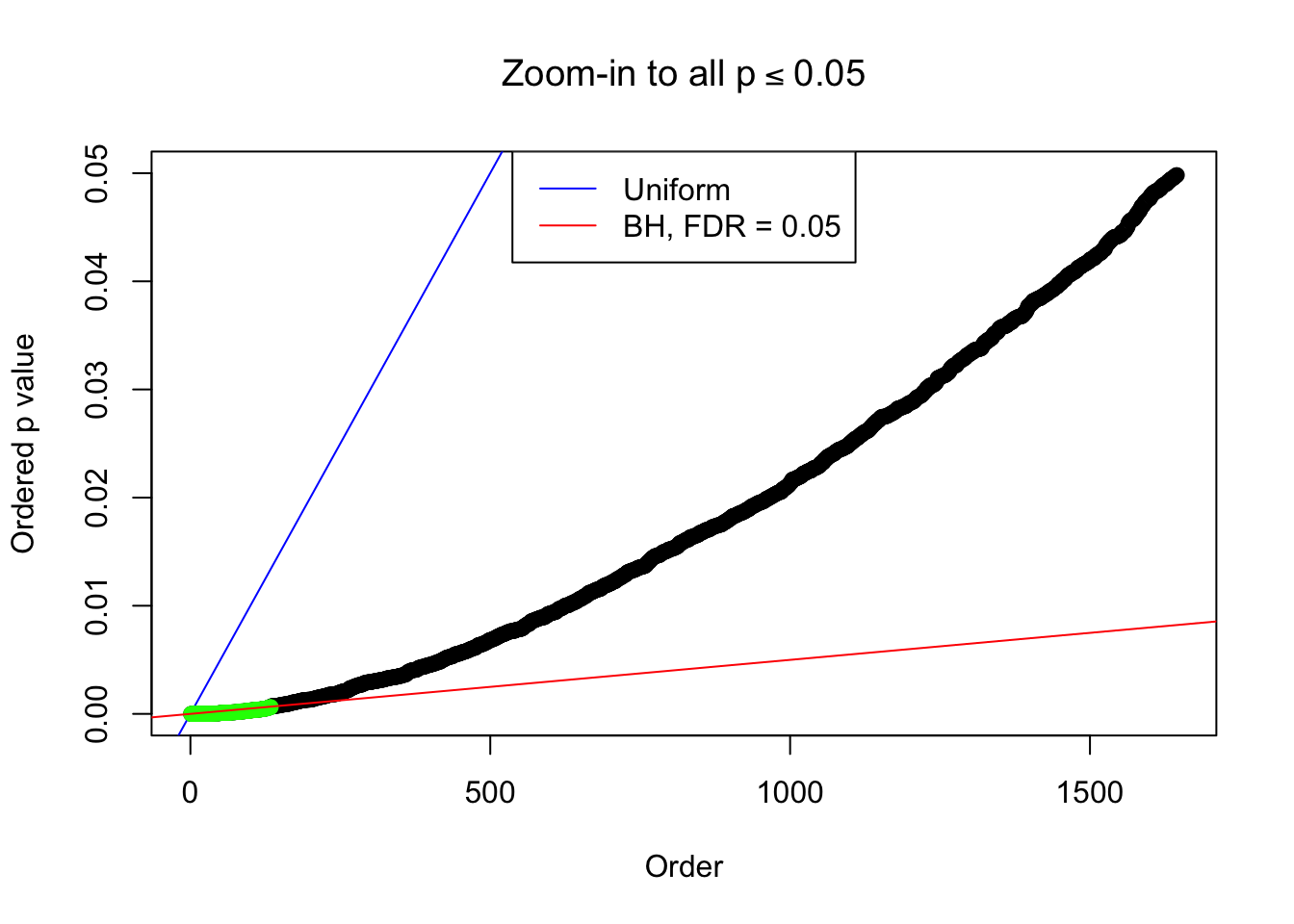
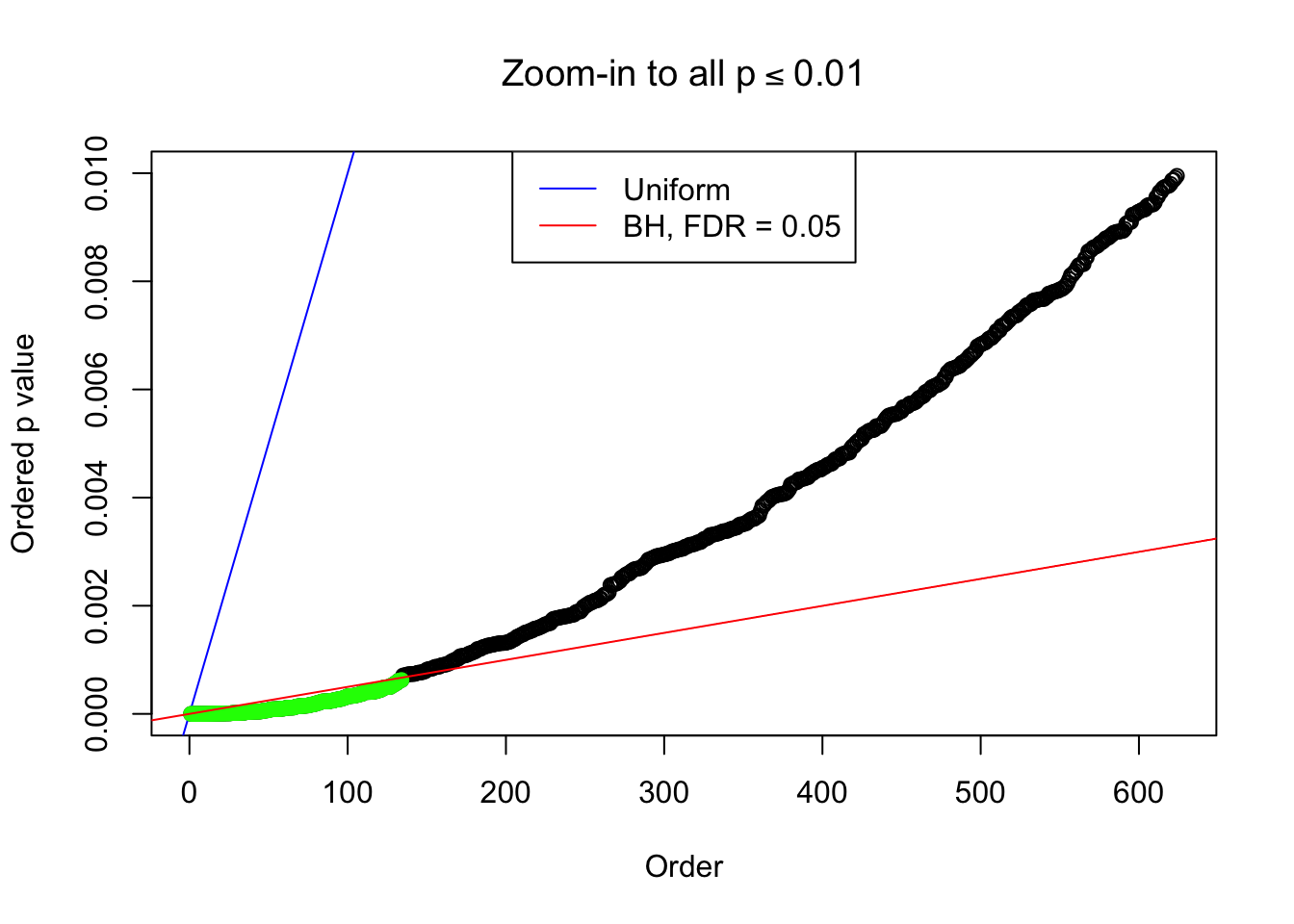
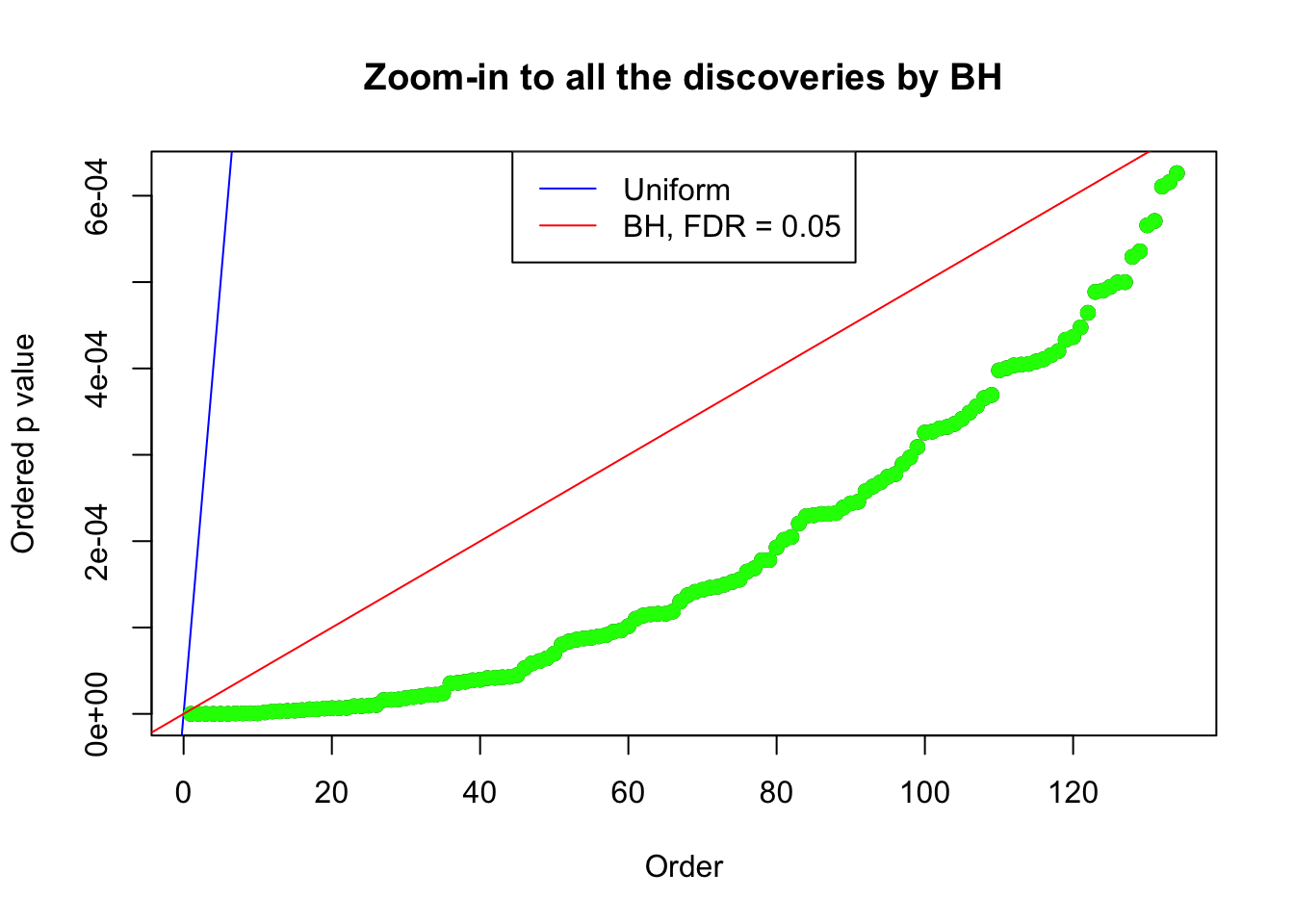
Example 5 : Number of Discoveries: 201 ; pihat0 = 0.3864133
Log-likelihood with N(0, 2): -17602.8
Log-likelihood with Gaussian Derivatives: -17607.36
Log-likelihood ratio between true N(0, 2) and fitted Gaussian derivatives: 4.565327
Normalized weights:
1 : -0.0149505230188178 ; 2 : 0.681006373173563 ; 3 : -0.029408092099831 ; 4 : 0.526597120212115 ; 5 : -0.0649823448928799 ; 6 : 0.248323484516014 ; 7 : -0.077154633635199 ;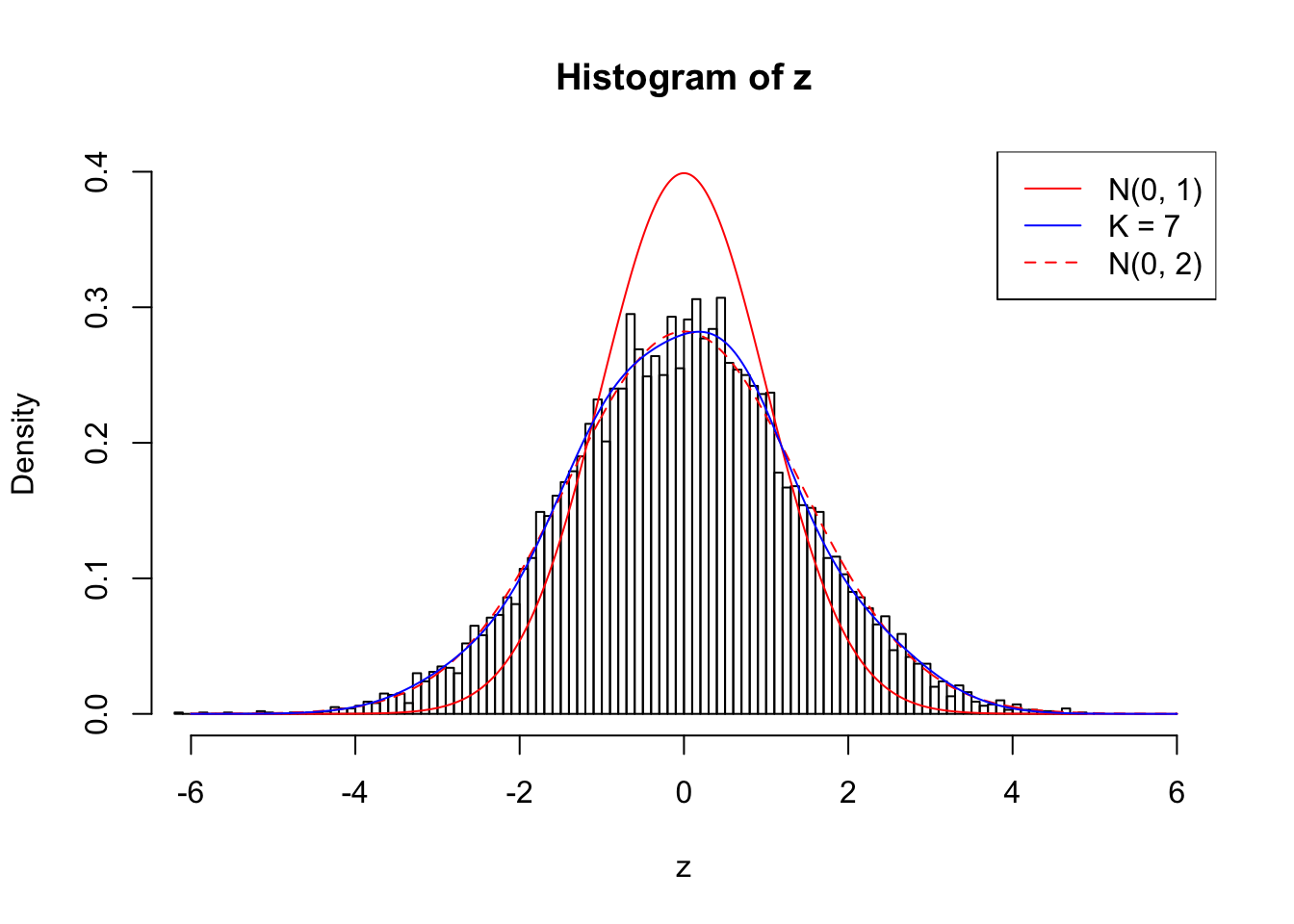
Zoom in to the left tail: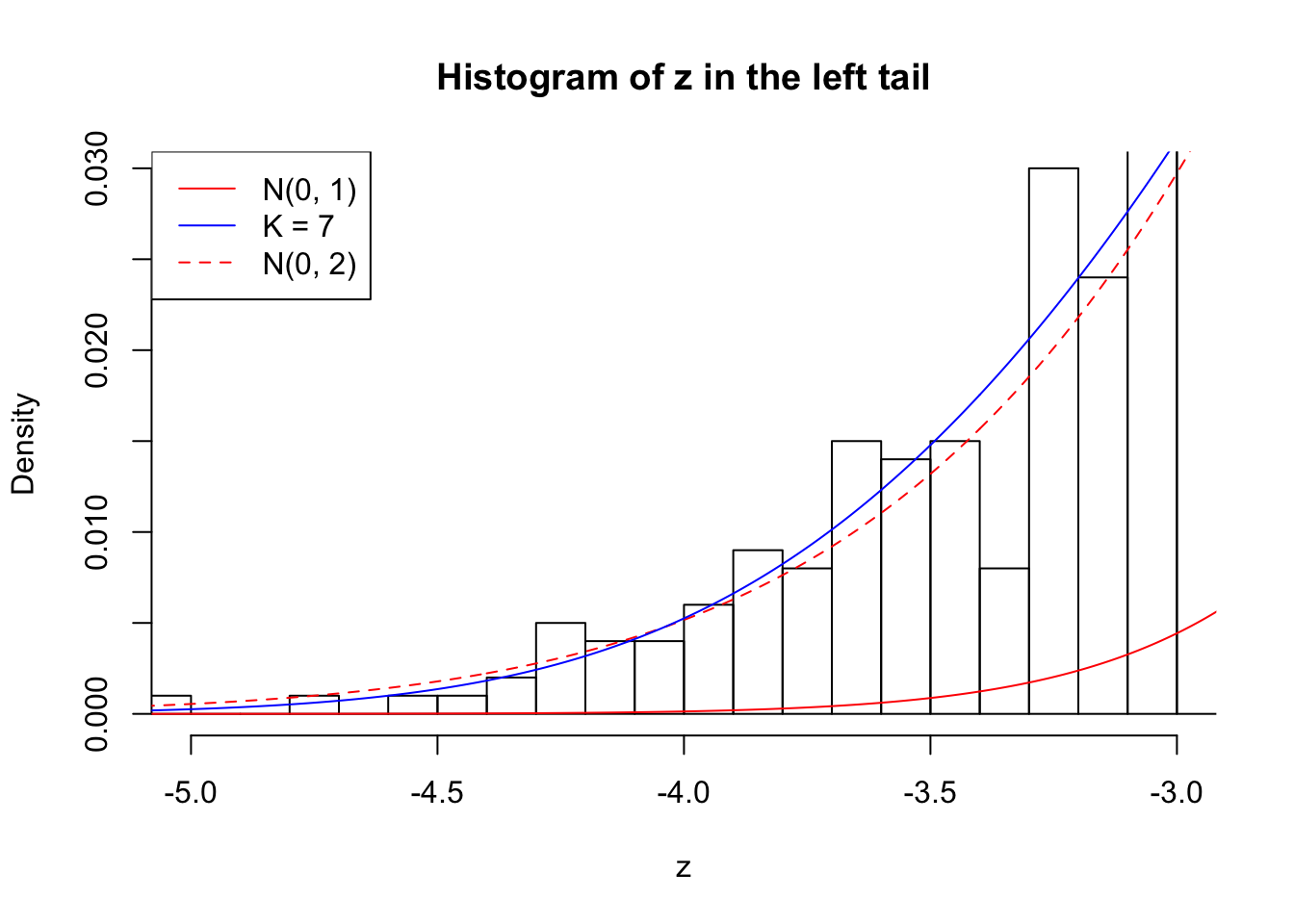
Zoom in to the right tail: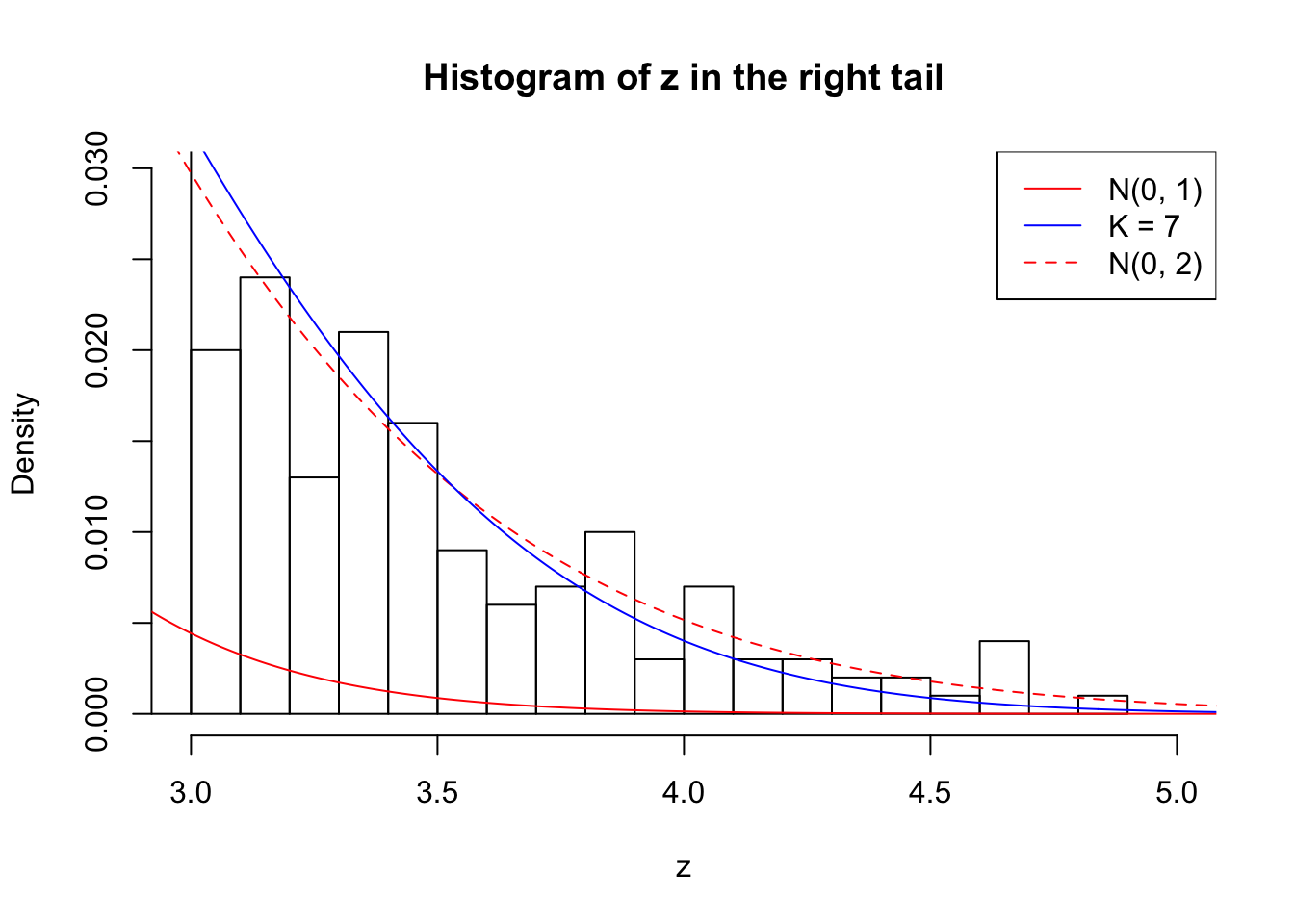
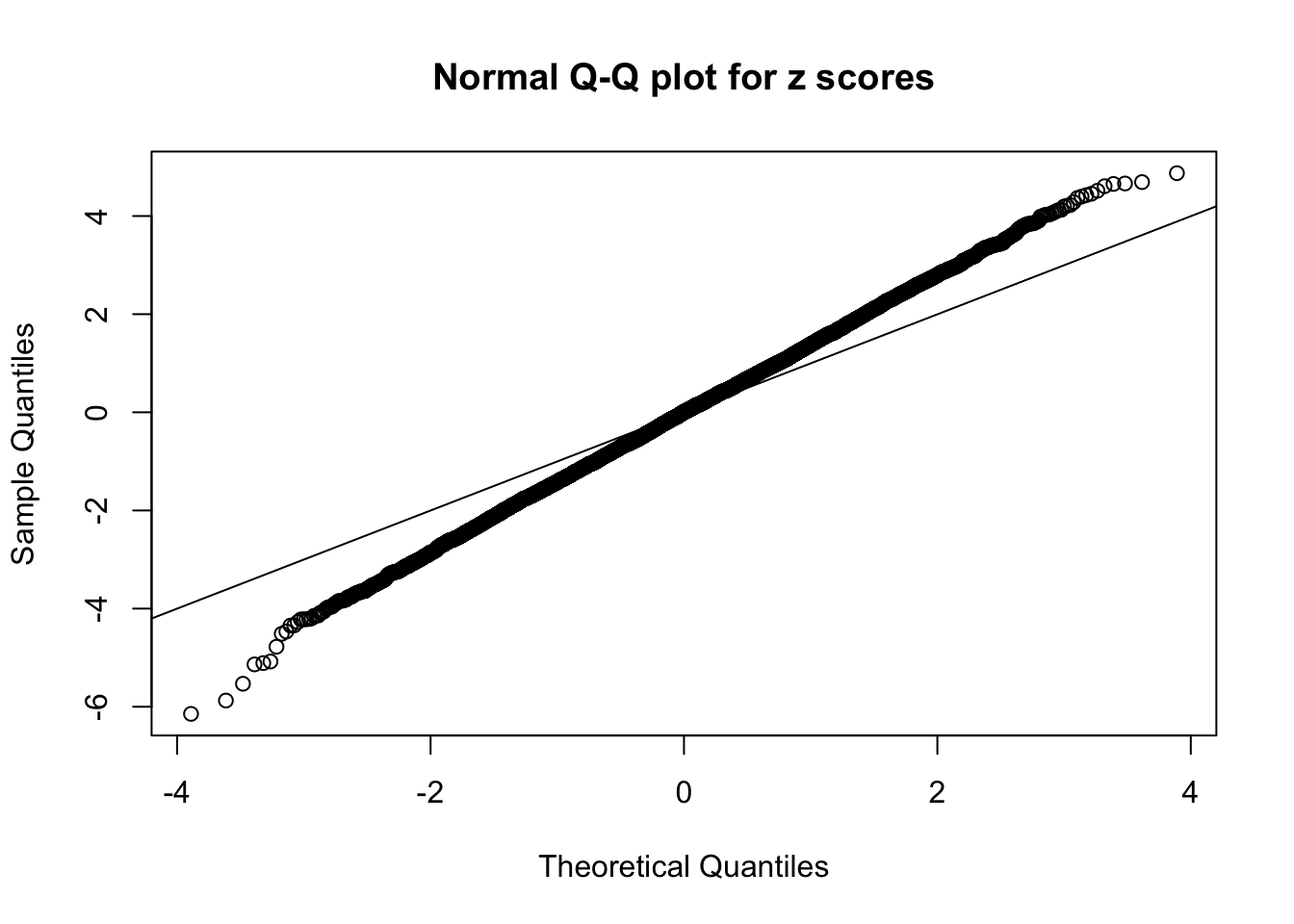
Session information
sessionInfo()R version 3.3.3 (2017-03-06)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: macOS Sierra 10.12.5
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] cvxr_0.0.0.9009 EQL_1.0-0 ttutils_1.0-1 ashr_2.1-13
loaded via a namespace (and not attached):
[1] Rcpp_0.12.10 knitr_1.16 magrittr_1.5
[4] REBayes_0.85 MASS_7.3-47 doParallel_1.0.10
[7] pscl_1.4.9 SQUAREM_2016.10-1 lattice_0.20-35
[10] R6_2.2.1 foreach_1.4.3 stringr_1.2.0
[13] tools_3.3.3 parallel_3.3.3 grid_3.3.3
[16] git2r_0.18.0 htmltools_0.3.6 iterators_1.0.8
[19] assertthat_0.2.0 yaml_2.1.14 rprojroot_1.2
[22] digest_0.6.12 Matrix_1.2-10 codetools_0.2-15
[25] evaluate_0.10 rmarkdown_1.5 stringi_1.1.5
[28] Rmosek_7.1.2 backports_1.0.5 truncnorm_1.0-7 This R Markdown site was created with workflowr