Simulating Design Matrix \(X\): Correlation patterns
Lei Sun
2018-02-05
Last updated: 2018-02-06
Code version: ee112bc
Introduction
For a fixed design matrix \(X\), \(\hat\beta \sim N(\beta, \sigma_e^2(X^TX)^{-1})\), and the empirical distribution of \(\hat z_j = \hat\beta_j / \hat{\text{SE}}(\hat\beta_j)\) under the null will depend on the average correlation in \((X^TX)^{-1}\).
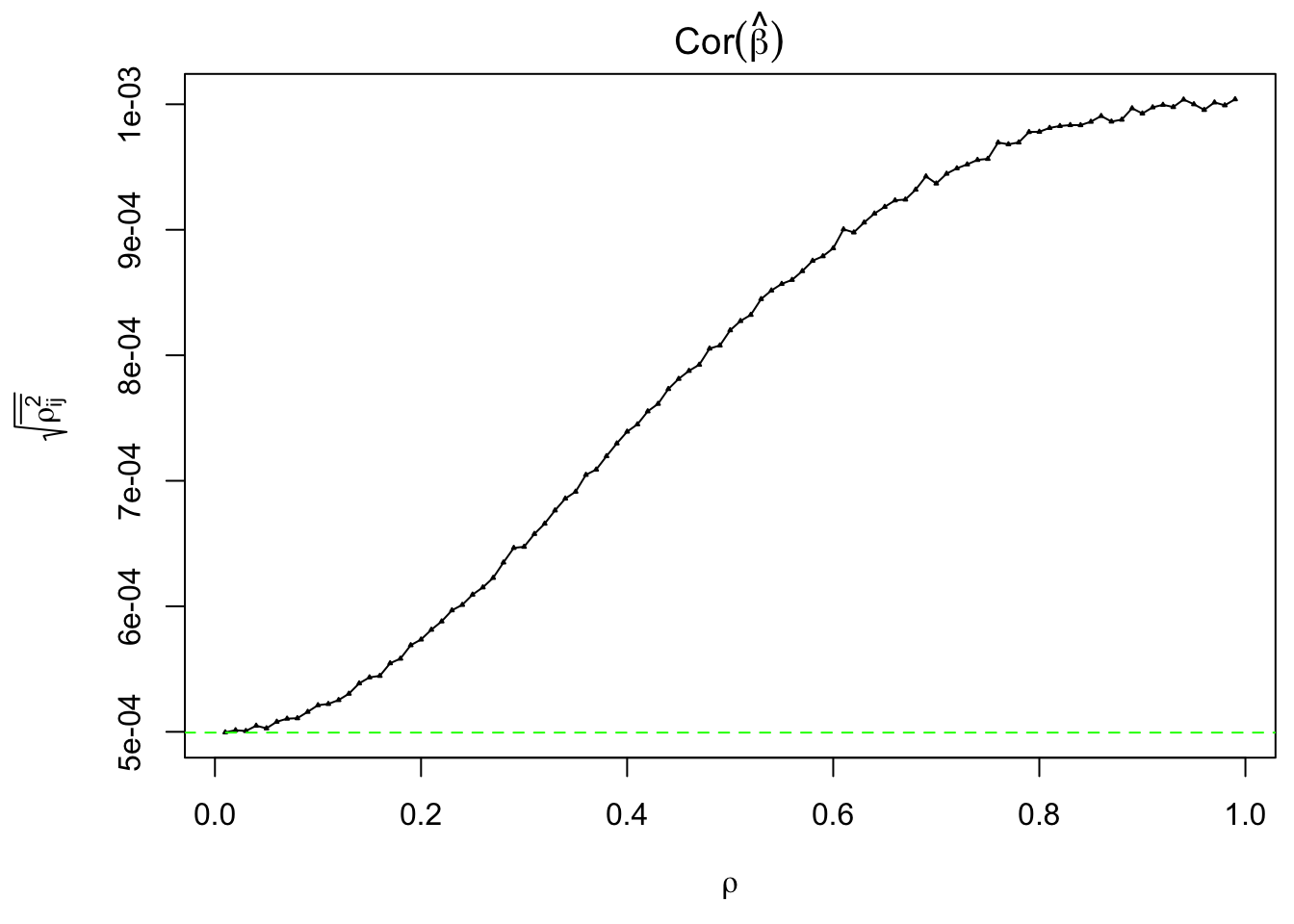
Actually the most important quantity to determine the shape of the empirical distribution of \(\hat z_j\) is the square root of the mean squared correlation among \(\hat\beta_j\)’s, that is, \(\sqrt{\overline{\rho_{\hat\beta_i, \hat\beta_j}^2}}\).
Now we are taking a look at this quantity for some commonly used design matrix in linear regression simulations.
In all three settings, each row of \(X_{n \times p}\) is independently drawn from a \(N(0, \Sigma)\) distribution, where the diagonal elements of \(\Sigma\) are all one. Then the columns of \(X\) are normalized such that \(\|X_j\|_2^2 = 1\).
Independent and normalized columns
- \(\Sigma = I\).

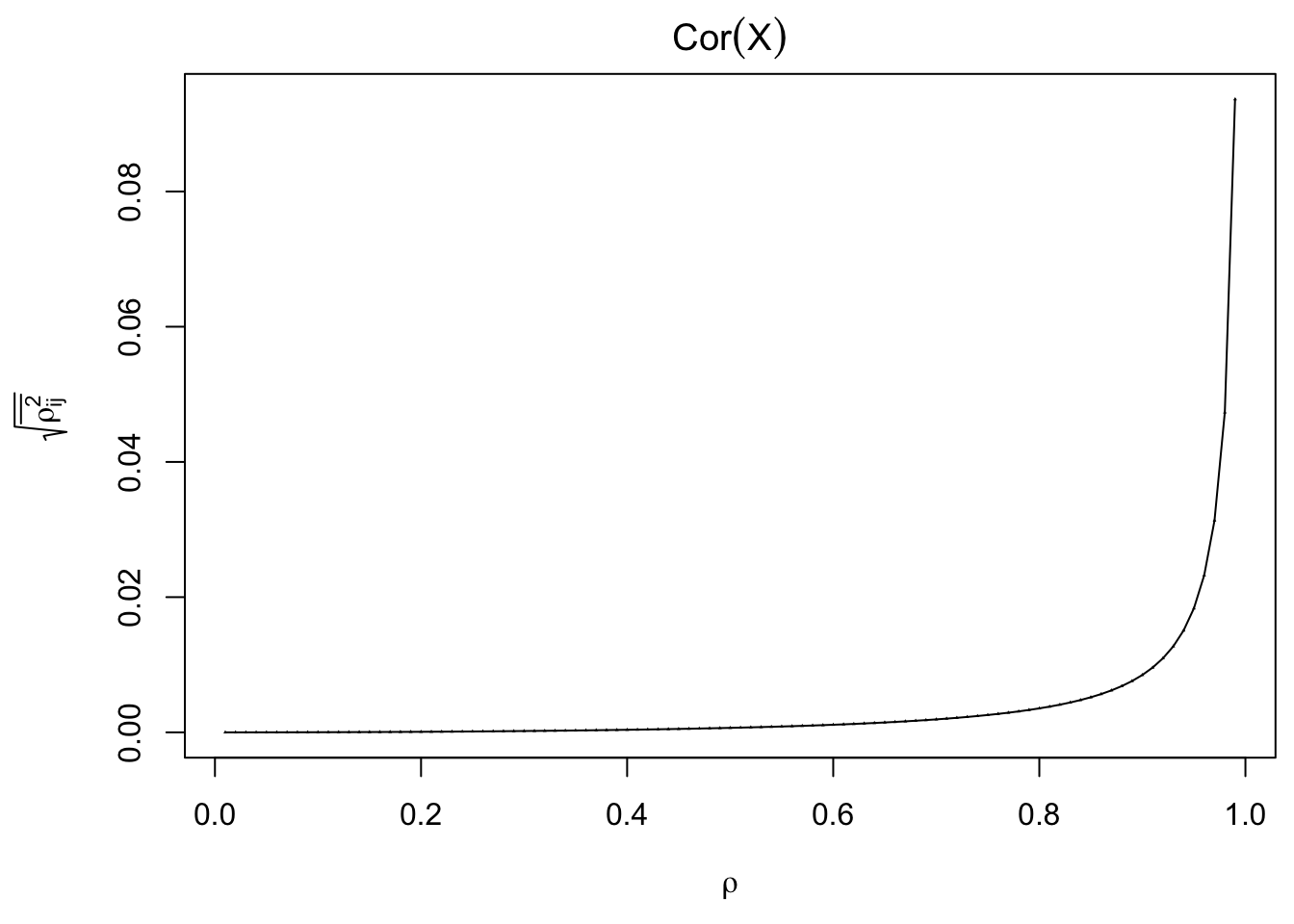
Toeplitz column correlation
- \(\Sigma_{ij} = \rho^{|i - j|}\)
\(\text{SE}\left(\hat\beta_j\right)\)
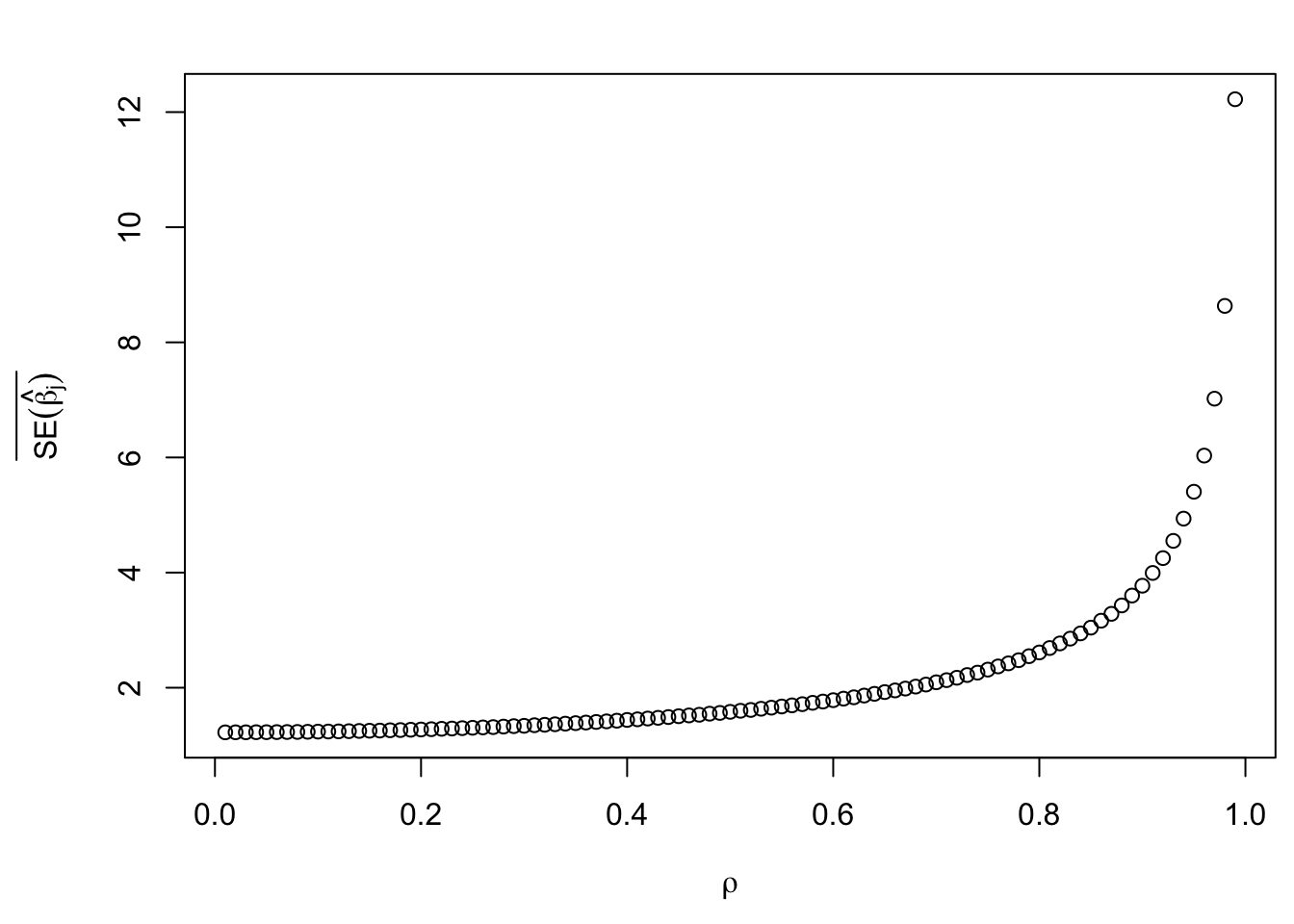

Average orrelation among \(X_j\) and \(\hat\beta_j\)
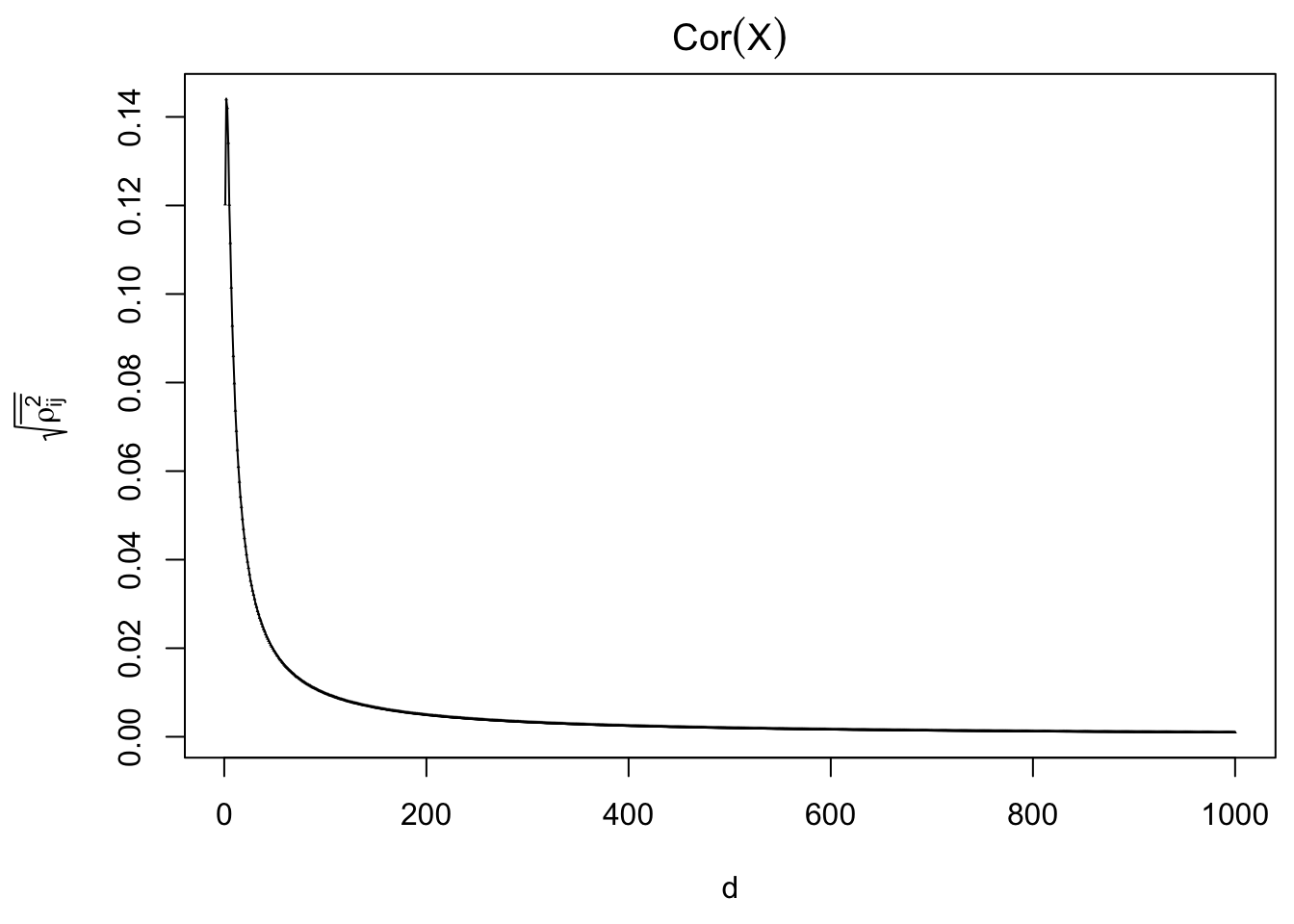
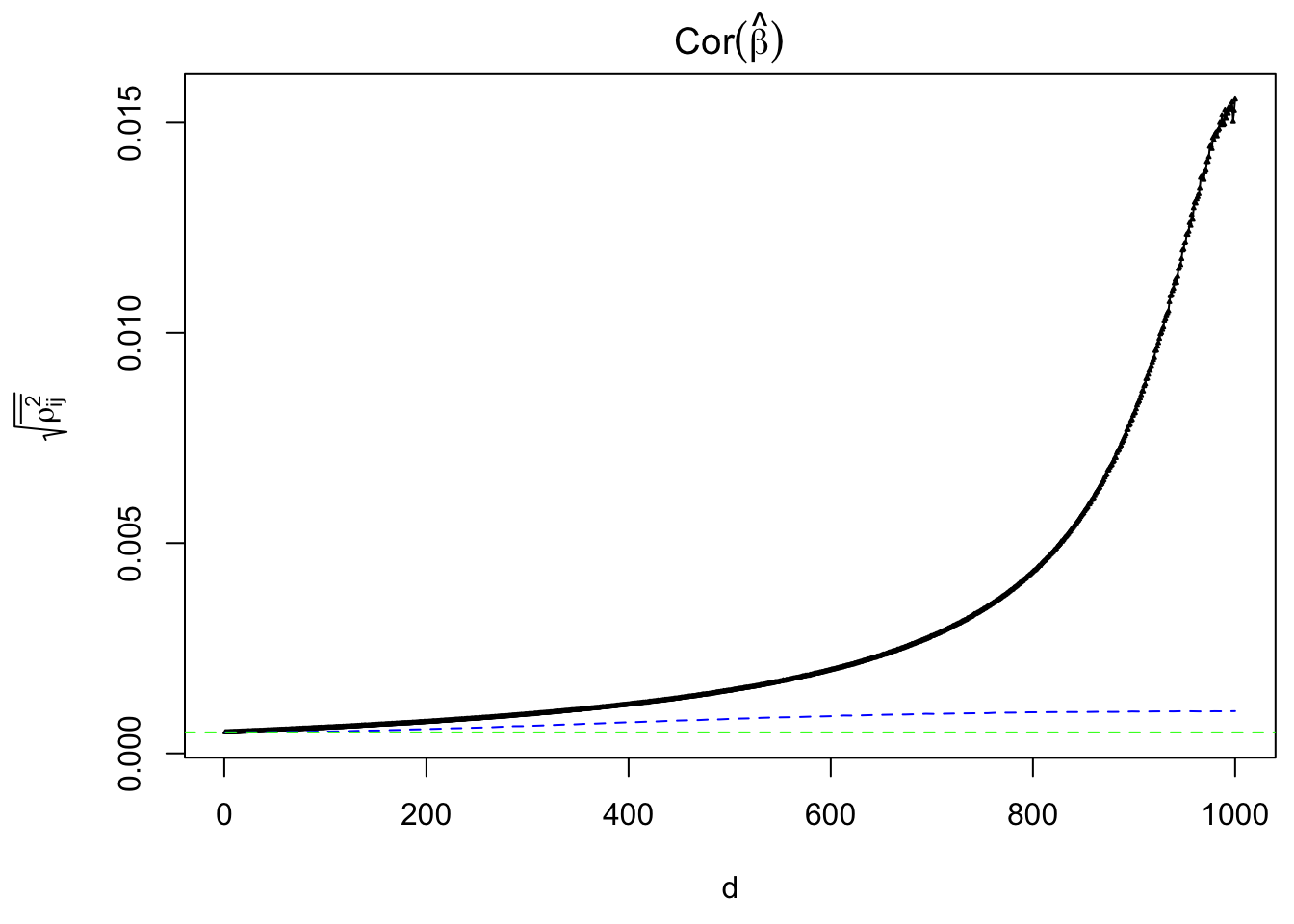
Factor model column correlation
- \(\Sigma = \texttt{cov2cor}(B_{p \times d}B_{d\times p}^T + I)\)
\(\text{SE}\left(\hat\beta_j\right)\)
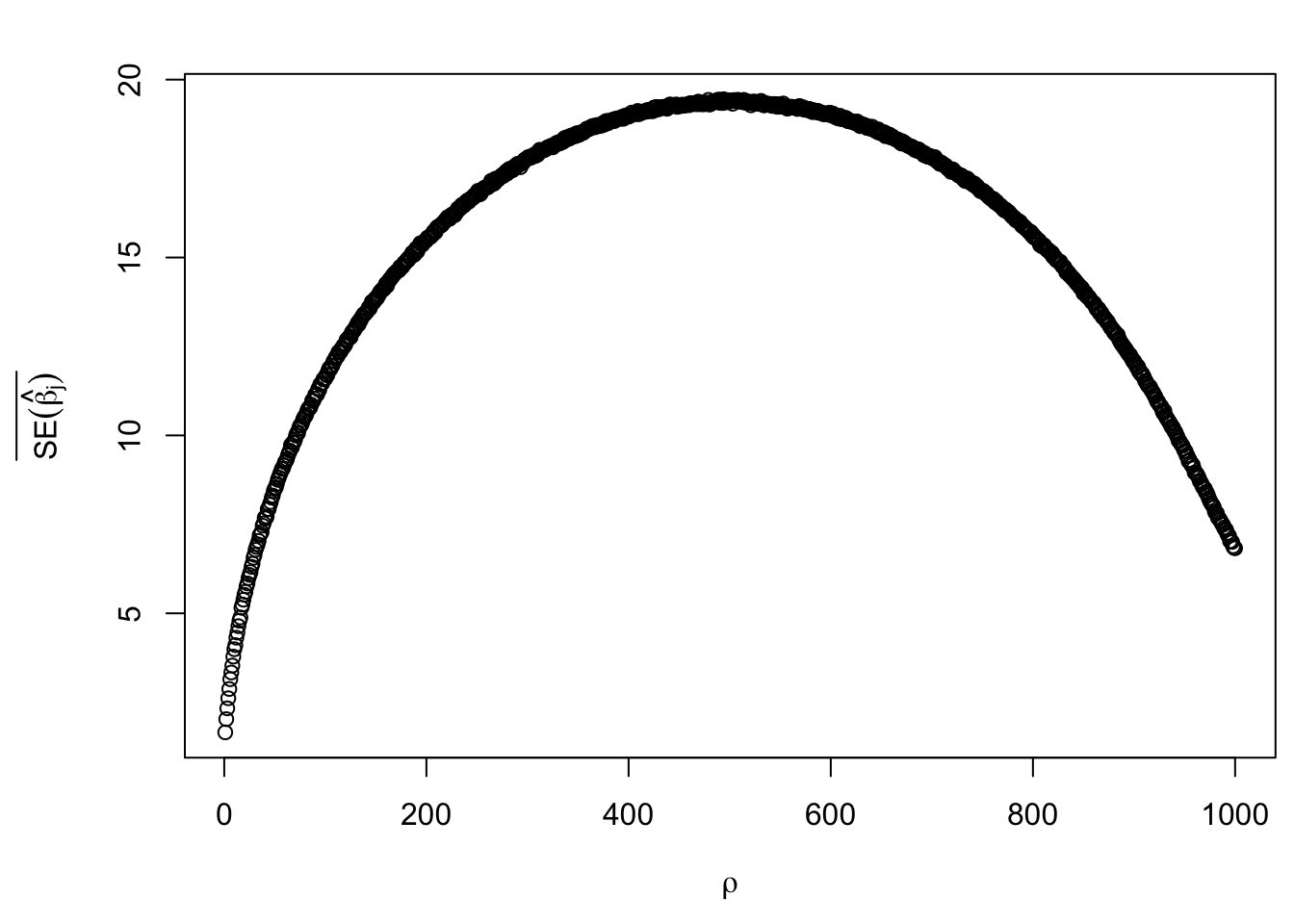
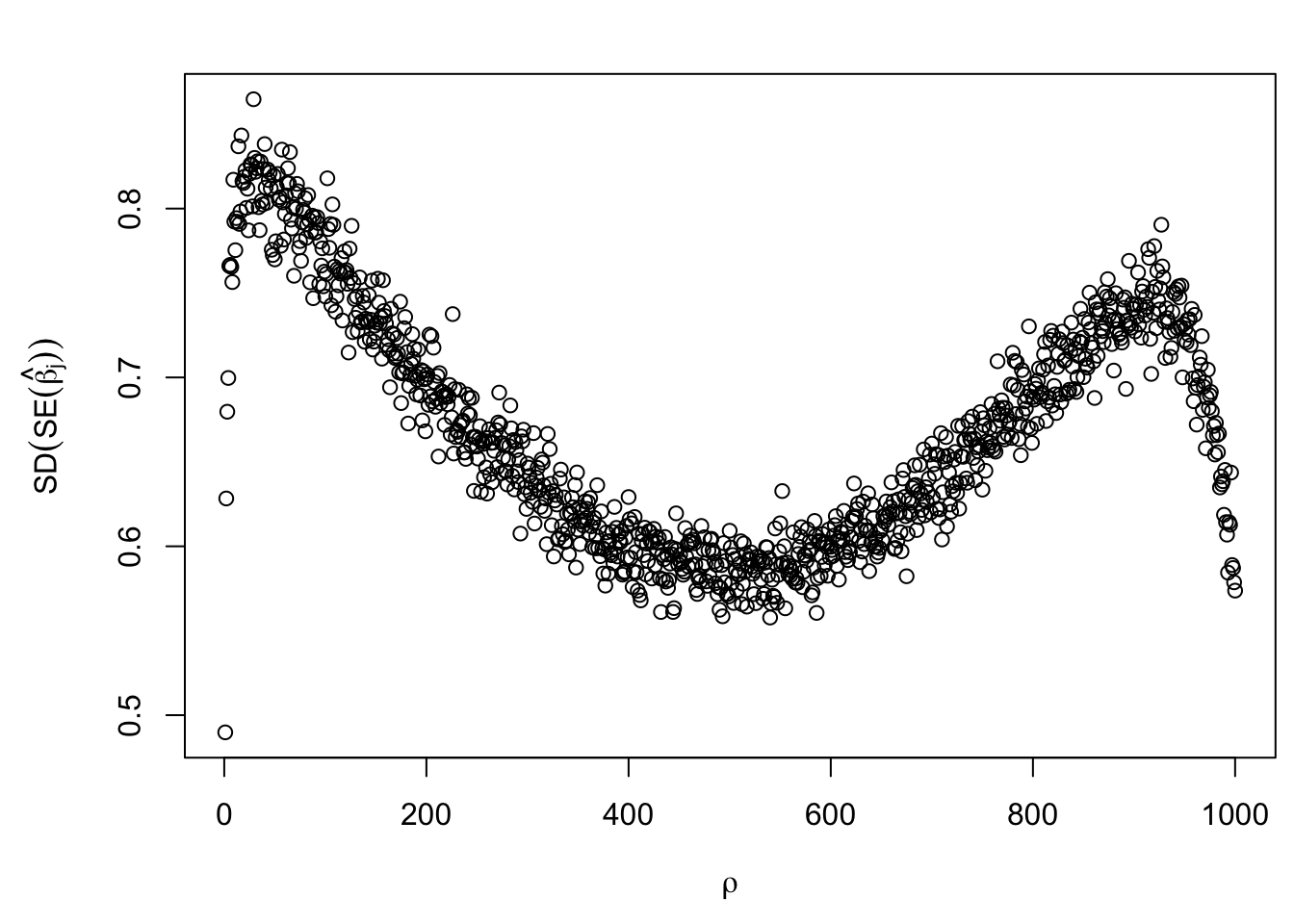
Average correlation among \(X_j\) and \(\hat\beta_j\).
Session information
sessionInfo()R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.2
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
loaded via a namespace (and not attached):
[1] compiler_3.4.3 backports_1.1.2 magrittr_1.5 rprojroot_1.3-2
[5] tools_3.4.3 htmltools_0.3.6 yaml_2.1.16 Rcpp_0.12.14
[9] stringi_1.1.6 rmarkdown_1.8 knitr_1.19 git2r_0.21.0
[13] stringr_1.2.0 digest_0.6.14 evaluate_0.10.1This R Markdown site was created with workflowr