Simulating Correlated \(N(0, 1)\) \(Z\) Scores
Lei Sun
2017-05-18
Last updated: 2017-11-07
Code version: 2c05d59
Introduction
Following Gao’s suggestion, we investigate whether Gaussian derivatives can fit the empirical distributions of purely synthetic correlated \(z\) scores simulated as follows.
\[ \begin{array}{rcl} z & = & L_{n \times k} x_k / \sqrt{\text{diag}\left(LL^T\right)} \ ;\\ k &\leq& n \ ; \\ l_{ij} & \sim & N\left(0, 1\right) \ ;\\ x_j & \sim & N\left(0, 1\right) \ ;\\ L & = & \begin{bmatrix} l_1^T \\ \vdots \\ l_n^T \\ \end{bmatrix}_{n \times k} \ ; \\ z_i & = & l_{i}^Tx / \sqrt{l_i^Tl_i} \ . \\ \end{array} \]
Fitting
The coefficients are not fitted by convex optimization, but by the method of moments. Namely, if a density \(f\) can be decomposed by Gaussian derivatives, \[ f\left(z\right) = \sum\limits_{l = 0}^L w_l \frac{1}{\sqrt{l!}}\varphi^{\left(l\right)}\left(z\right) \ , \] then due to the orthonormality of normalized Hermite polynomials, \(w_l\) can be expressed as \[ w_l = \left(-1\right)^l\frac{1}{\sqrt{l!}}\int h_l\left(z\right)f\left(z\right)dz \ . \] Since \(h_l\)’s are polynomials, \(w_l\) is a linear combination of moments under \(f\), and can thus be estimated by sample moments, also called Hermite moments.
Examples
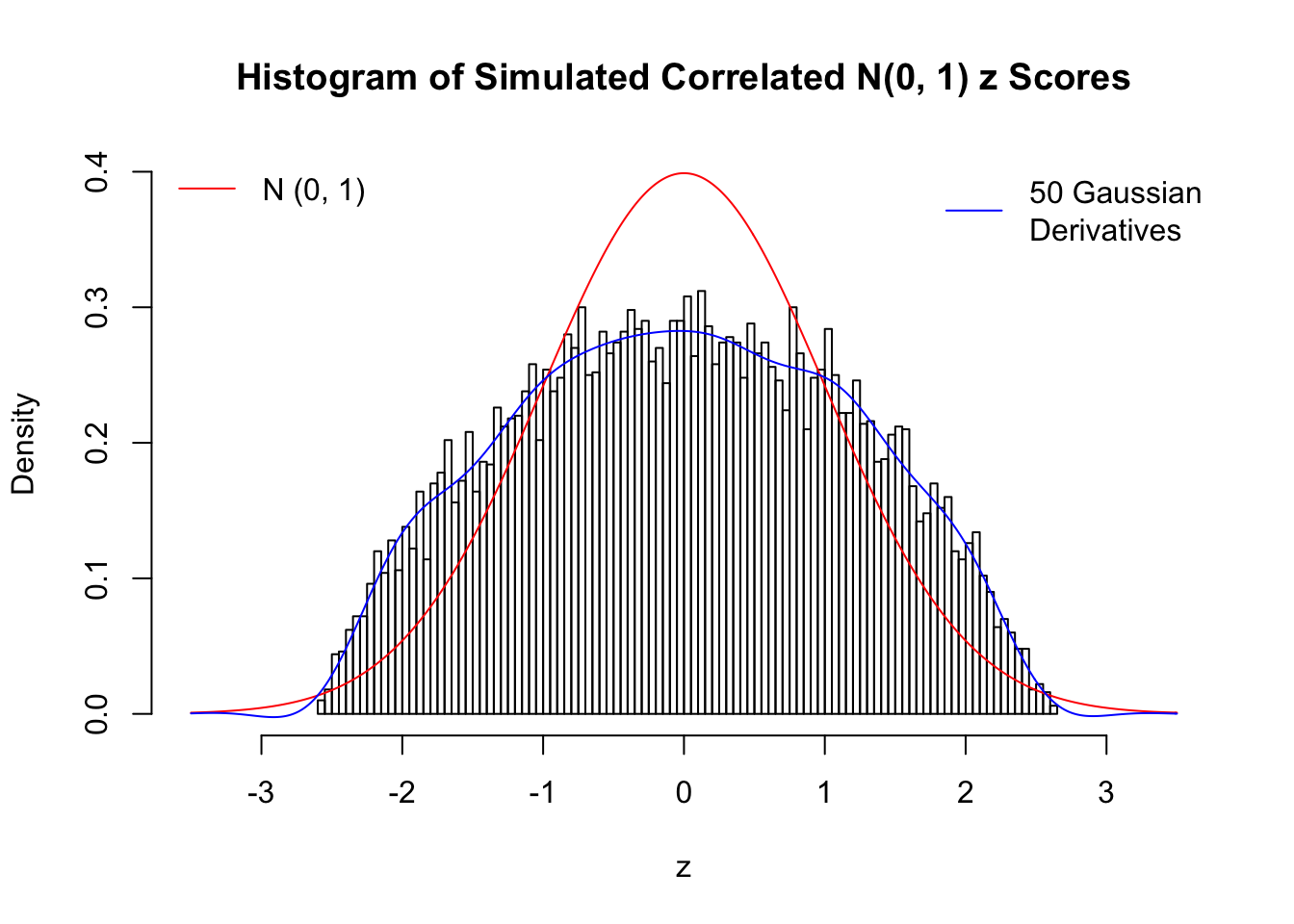
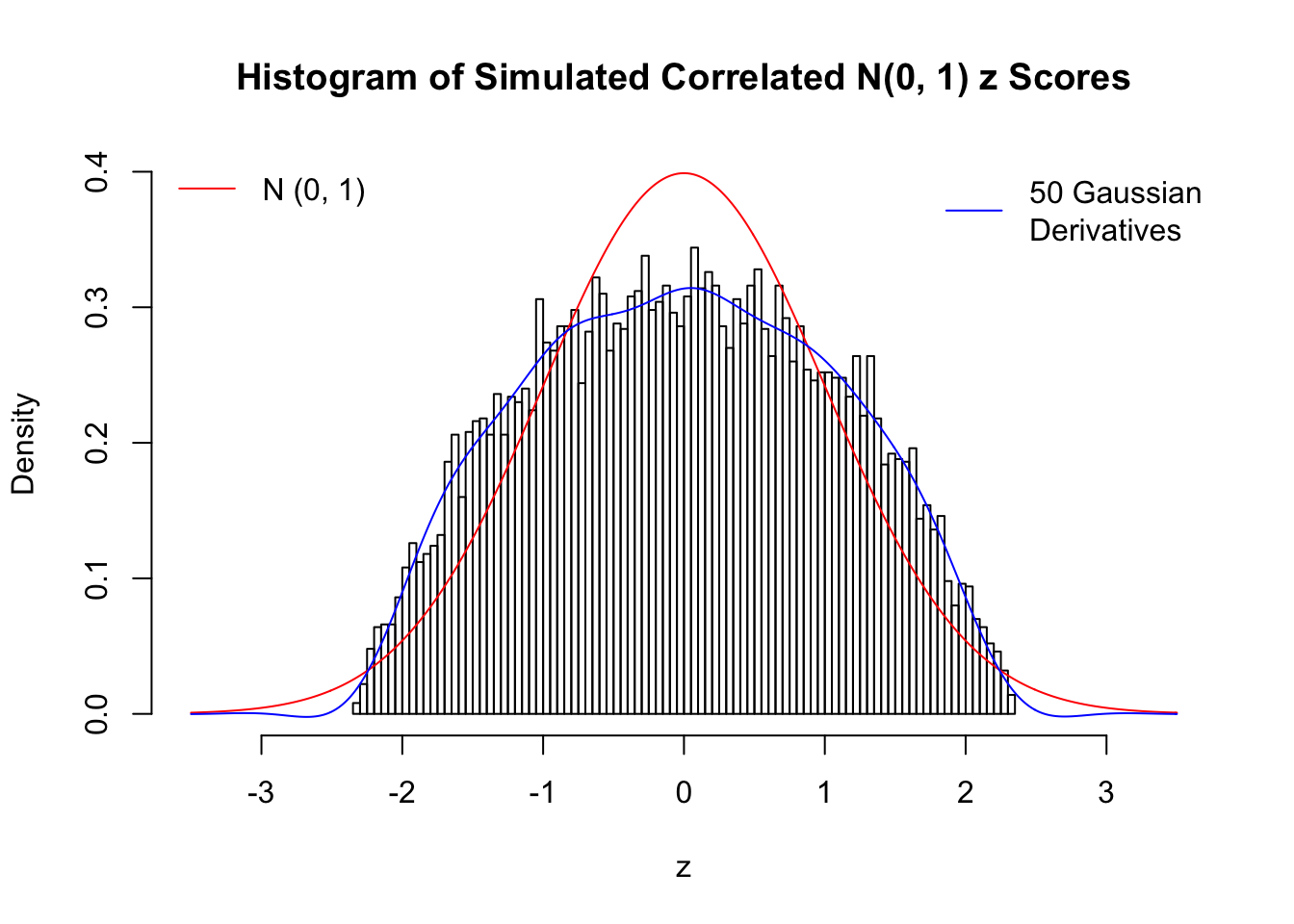
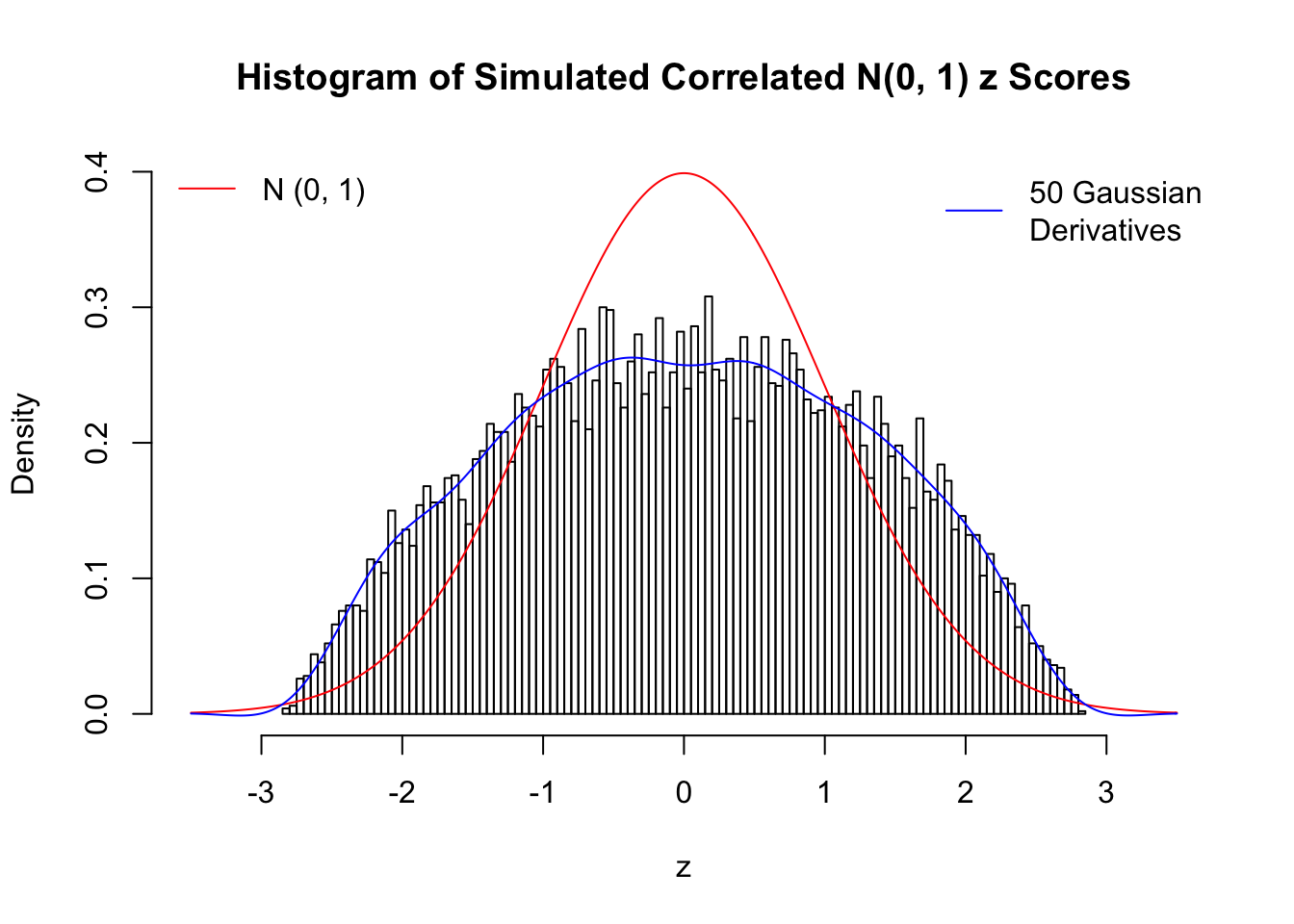
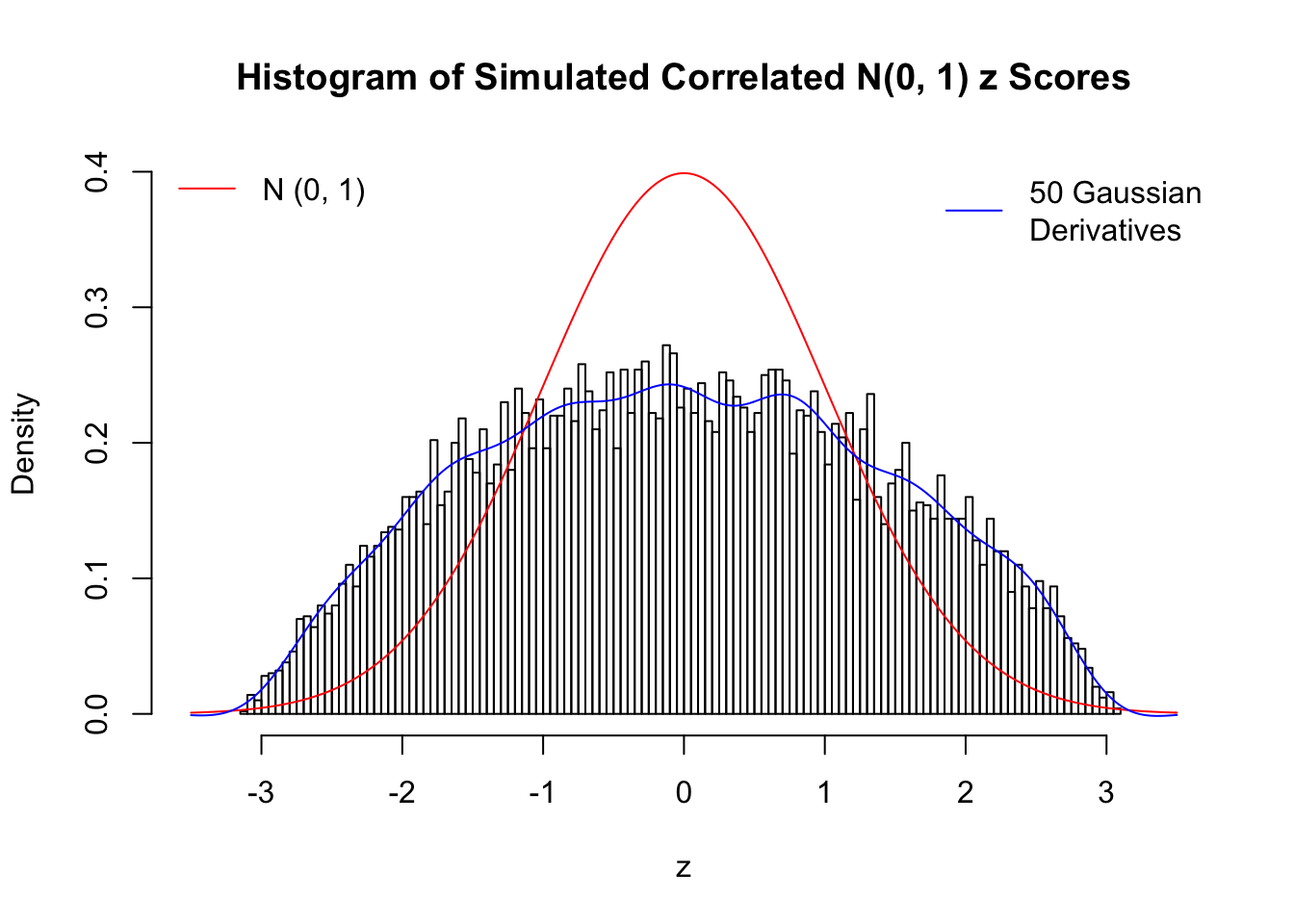
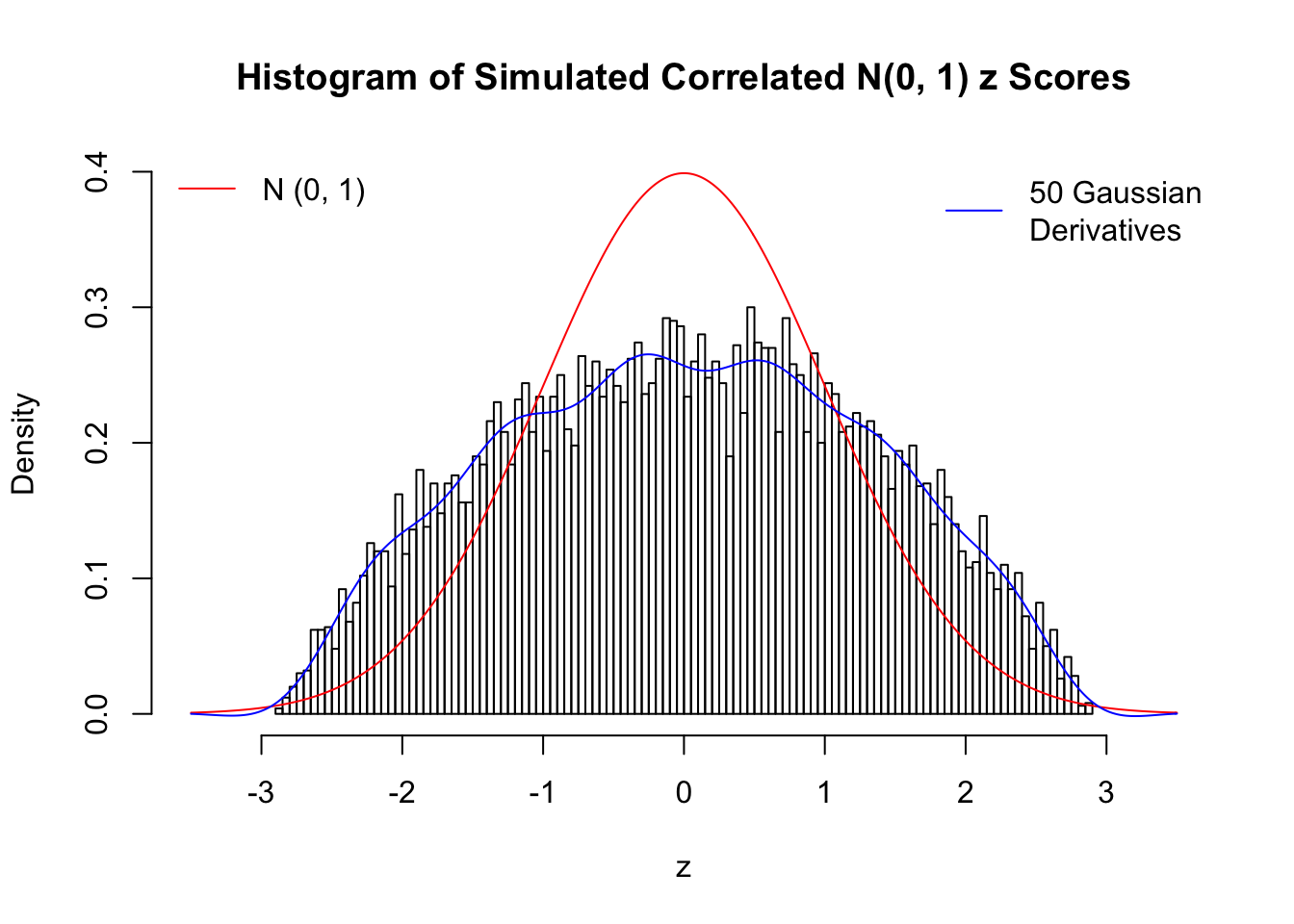
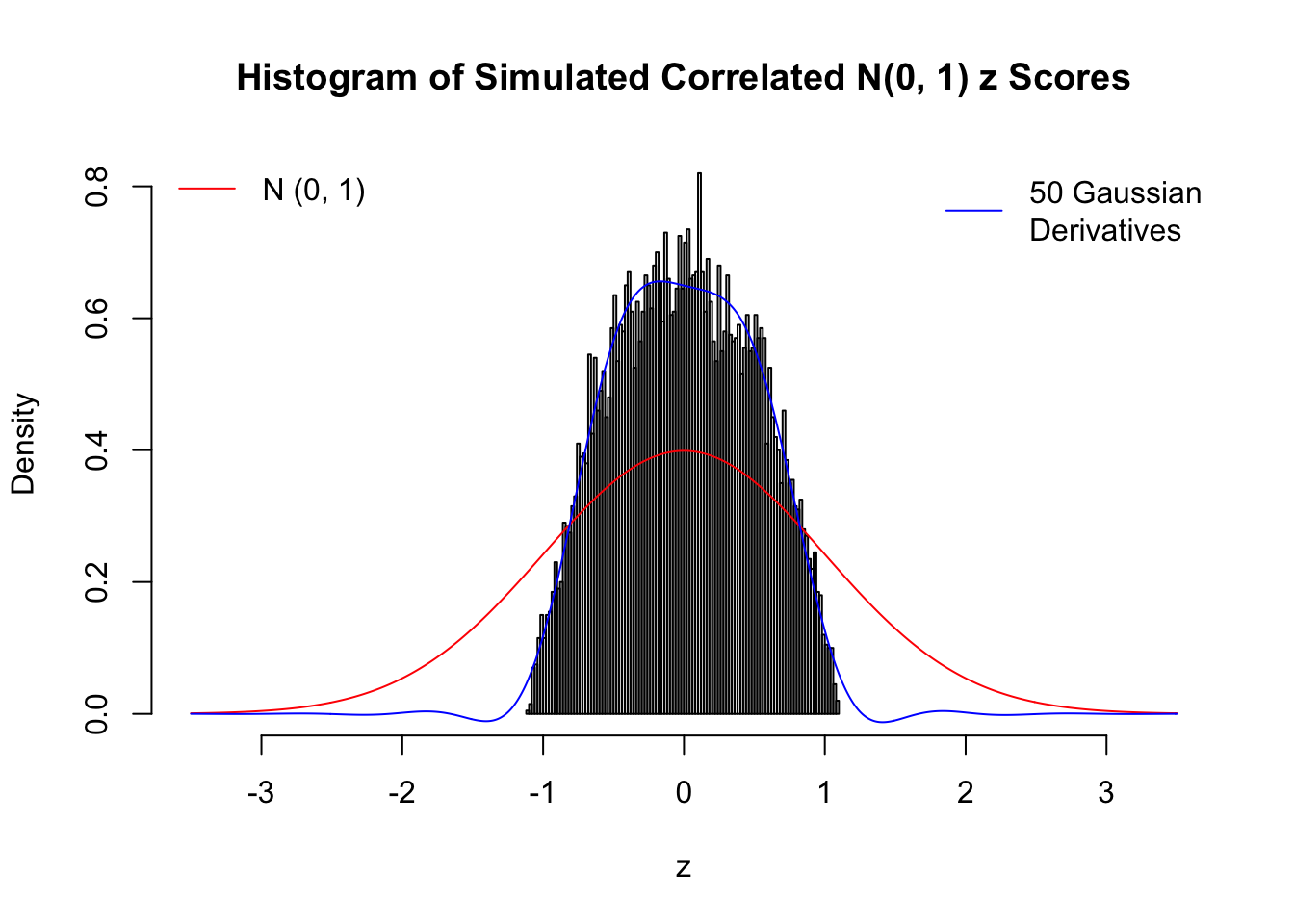
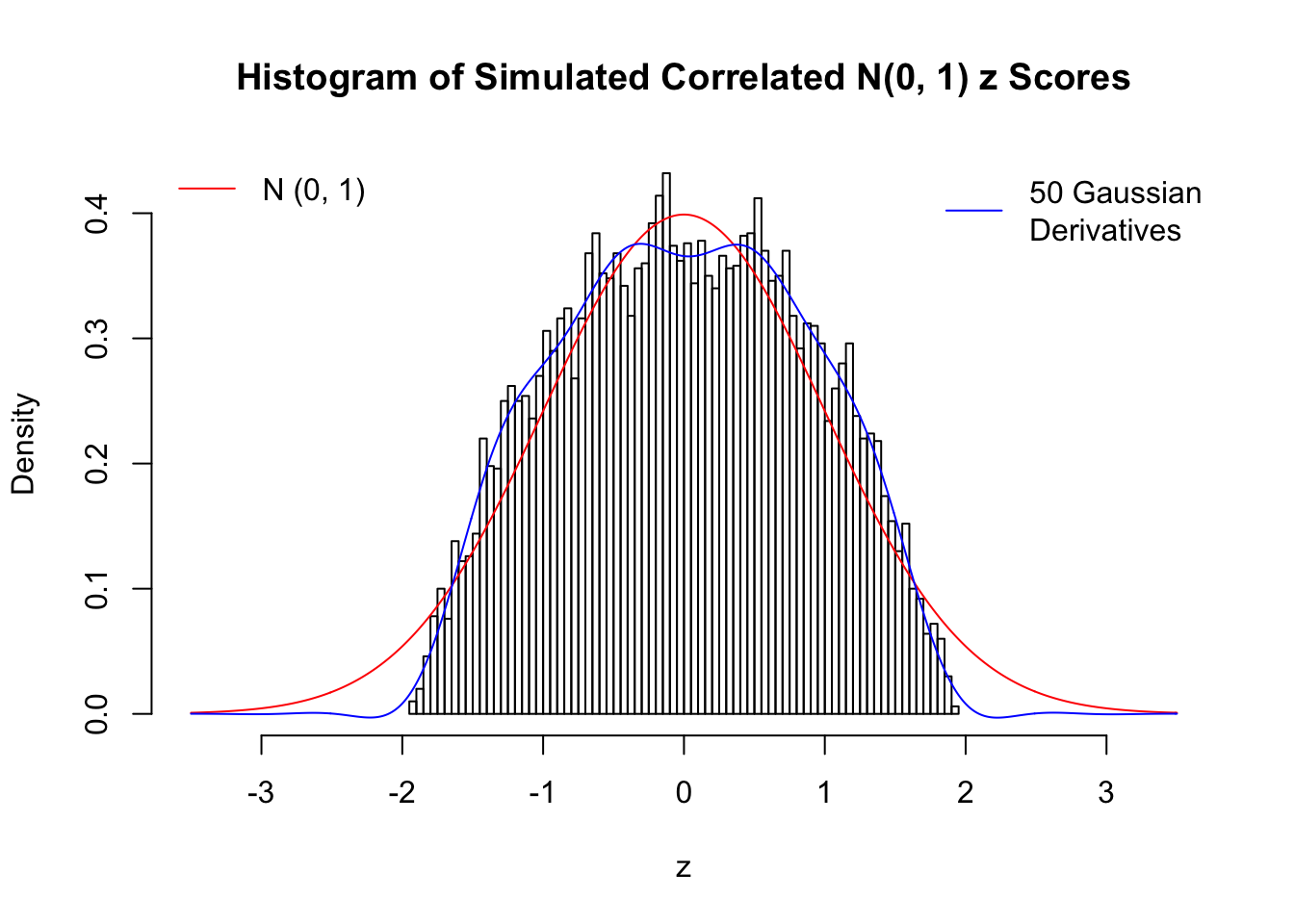
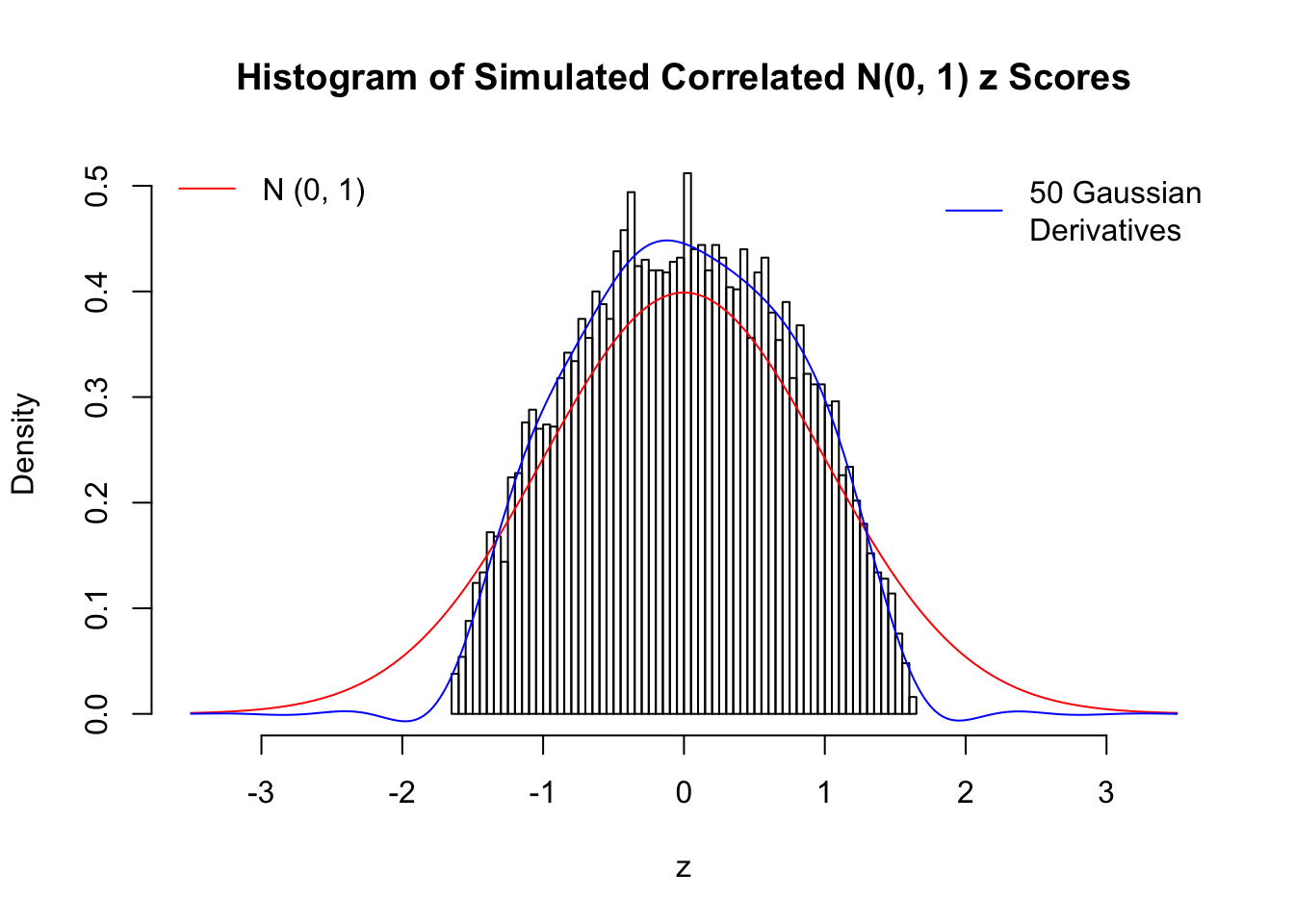
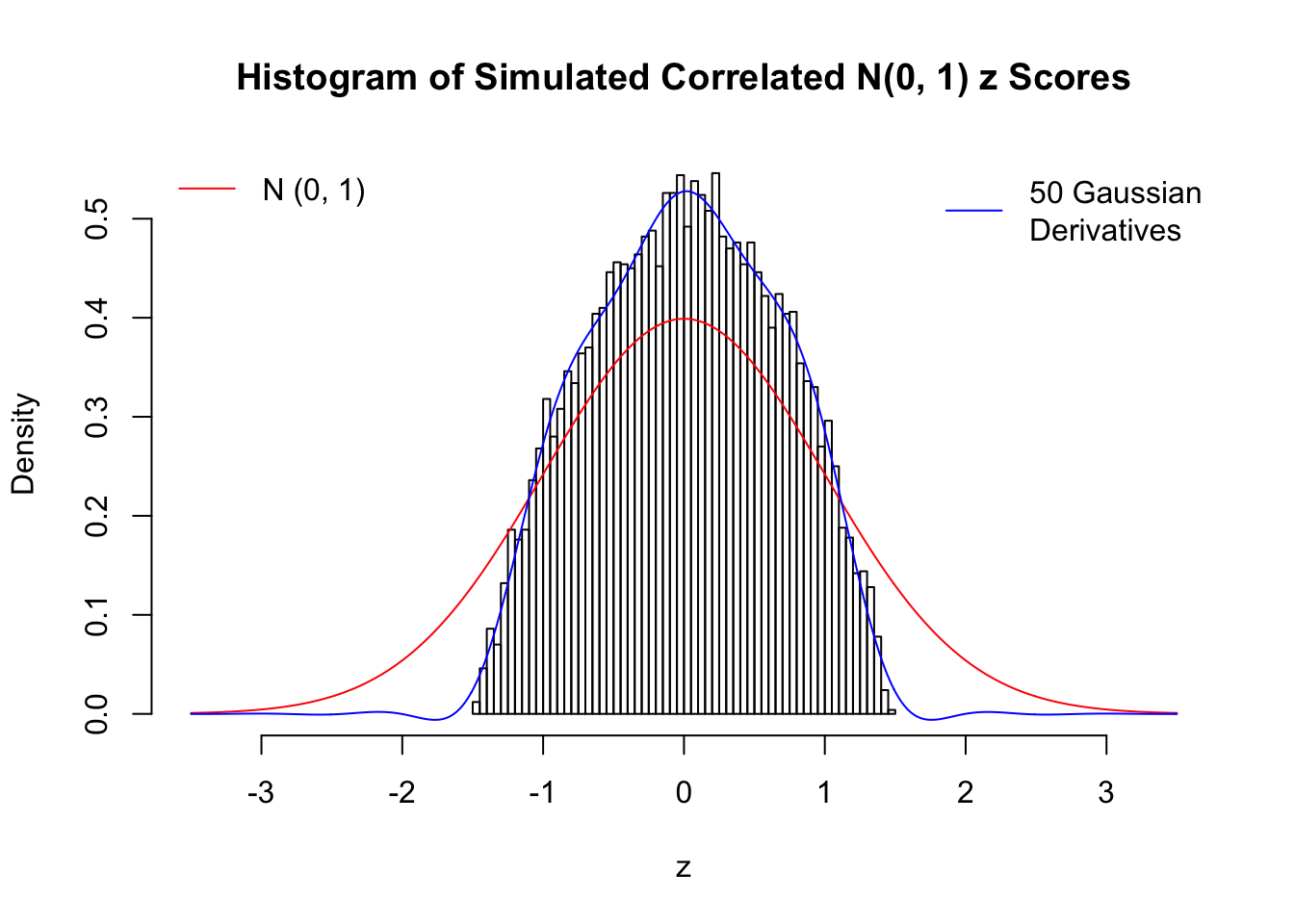
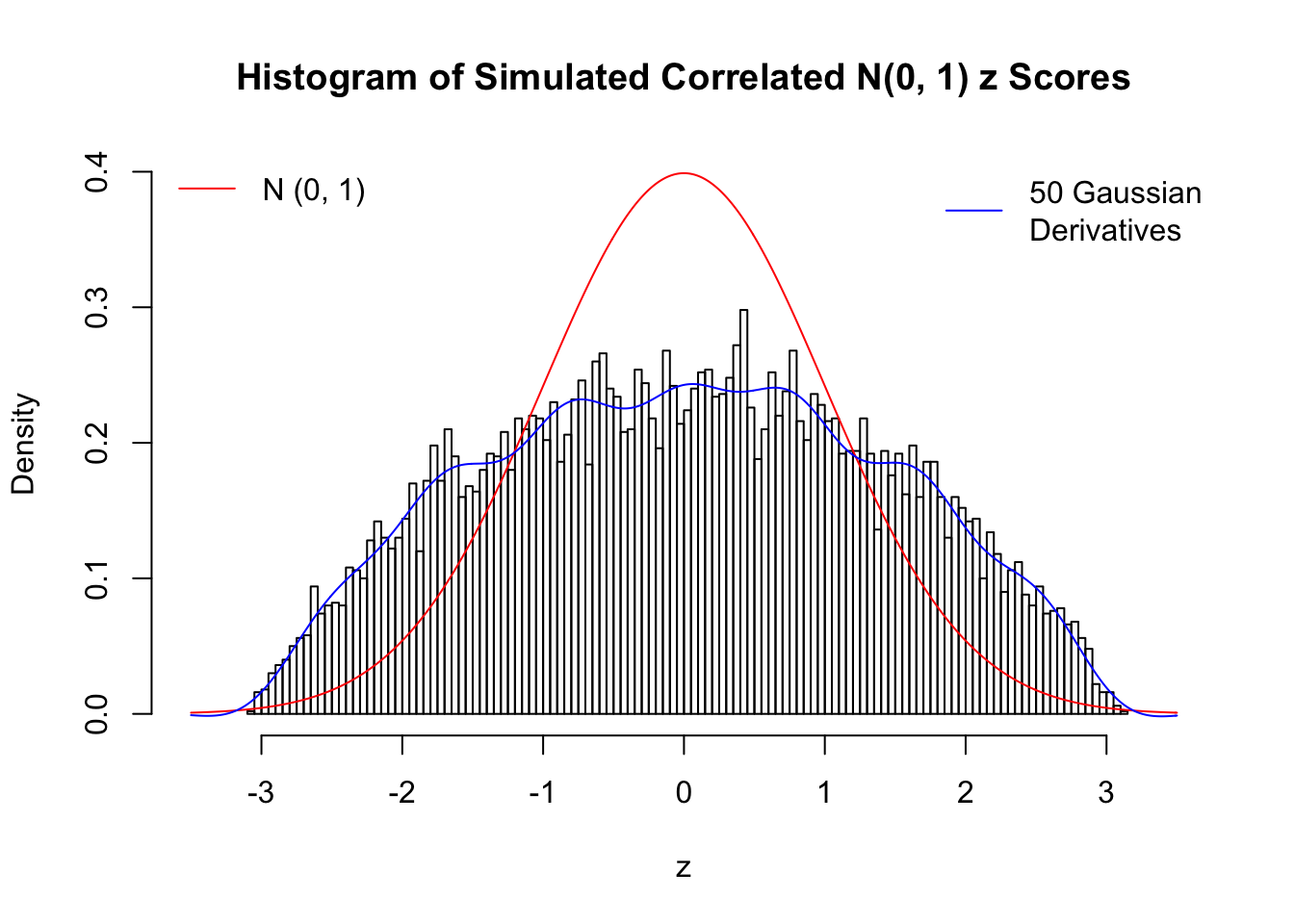
Remarks
The coefficients \(\hat w_l\) estimated by the method of moments are not very satisfying even with \(50\) Gaussian derivatives. The reason might be that completely synthetic correlated data are less likely to have samples on the extreme tails, as observed in the histograms, yet these extreme samples are supposed to have disproportional influence on the method of moments estimates. We also tried to estimate \(\hat w_l\) by the convex optimization approach, but the results were even worse, probably due to the same reason. The results might indicate an interesting but often neglected difference between real data and synthetic ones.
Session information
sessionInfo()R version 3.4.2 (2017-09-28)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS Sierra 10.12.6
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
loaded via a namespace (and not attached):
[1] compiler_3.4.2 backports_1.1.1 magrittr_1.5 rprojroot_1.2
[5] tools_3.4.2 htmltools_0.3.6 yaml_2.1.14 Rcpp_0.12.13
[9] stringi_1.1.5 rmarkdown_1.6 knitr_1.17 git2r_0.19.0
[13] stringr_1.2.0 digest_0.6.12 evaluate_0.10.1This R Markdown site was created with workflowr