Approximating the Delta function by Gaussian Derivatives
Lei Sun
2017-05-10
Last updated: 2017-05-11
Code version: 3501eca
Introduction
Theoretically, the Dirac delta function \(\delta_z\) can be approximated by infinite orders of Gaussian derivatives as follows,
\[
\delta_z = \sum\limits_{l = 0}^\infty \frac{1}{\sqrt{l!}}h_l\left(z\right)
\left(\frac{1}{\sqrt{l!}}h_l\left(x\right)\varphi(x)\right) \ .
\] Previously with the EQL::hermite function, it takes a very long time to evaluate an Hermite polynomial of a high degree, yet the PolynomF package provides a computationally efficient way to check if higher order Gaussian derivatives indeed approximate \(\delta_z\) at any \(z\).
With finite \(L\), we are looking at
\[ f_L\left(x\right) := \sum\limits_{l = 0}^L \frac{1}{\sqrt{l!}}h_l\left(z\right) \left( \frac{1}{\sqrt{l!}}h_l\left(x\right) \varphi\left(x\right) \right) \] and
\[ F_L\left(x\right) := \Phi\left(x\right) - \sum\limits_{l = 1}^L \frac{1}{\sqrt{l}} \frac{1}{\sqrt{l!}}h_l\left(z\right) \left( \frac{1}{\sqrt{\left(l - 1\right)!}}h_{l - 1}\left(x\right)\varphi\left(x\right)\right) \ . \] Given any \(z\), \(f_L\) should get closer to \(\delta_z\) and \(F_L\) to the \(0\)-\(1\) step function, as \(L\to\infty\).
\(z = -2\)
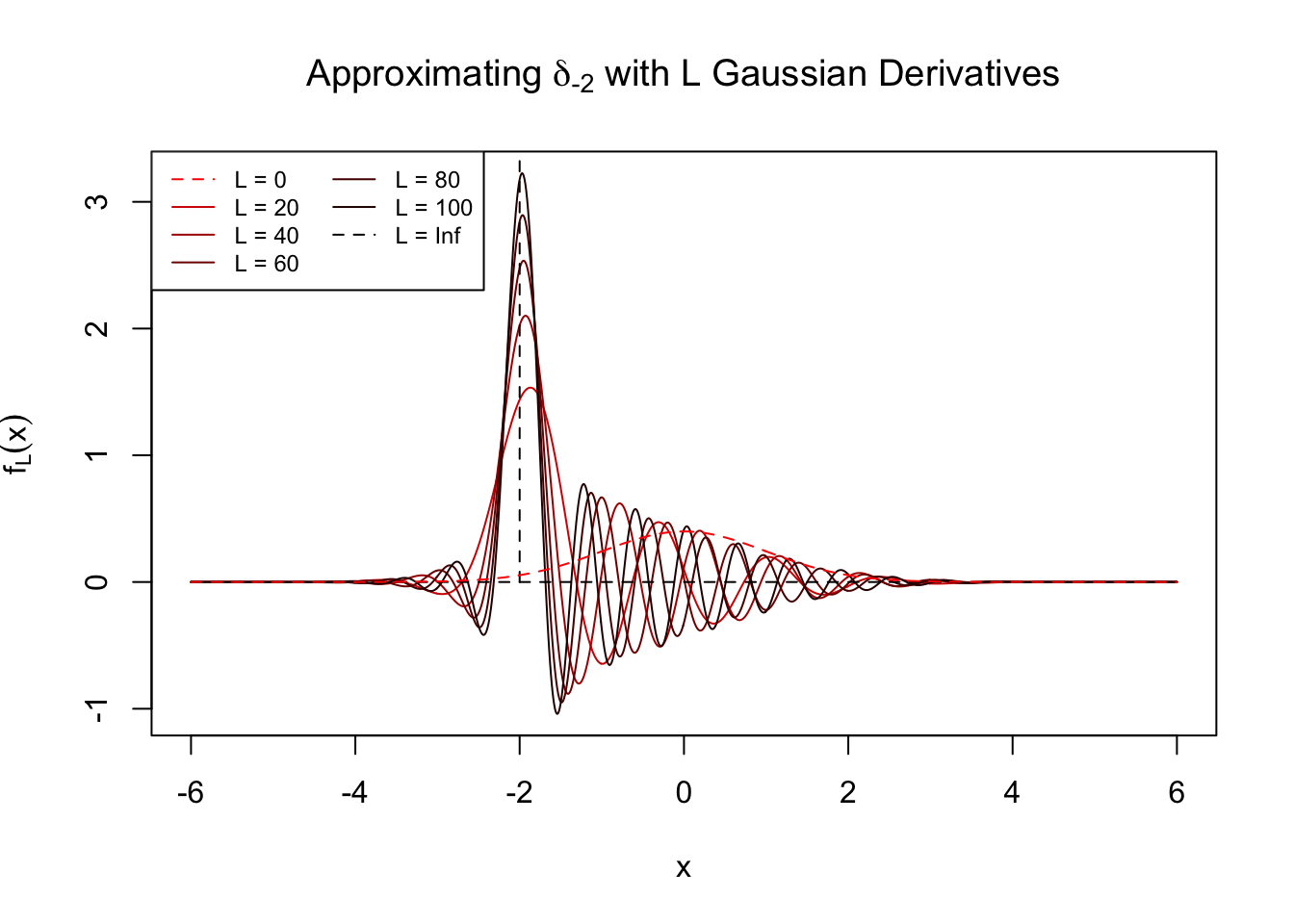
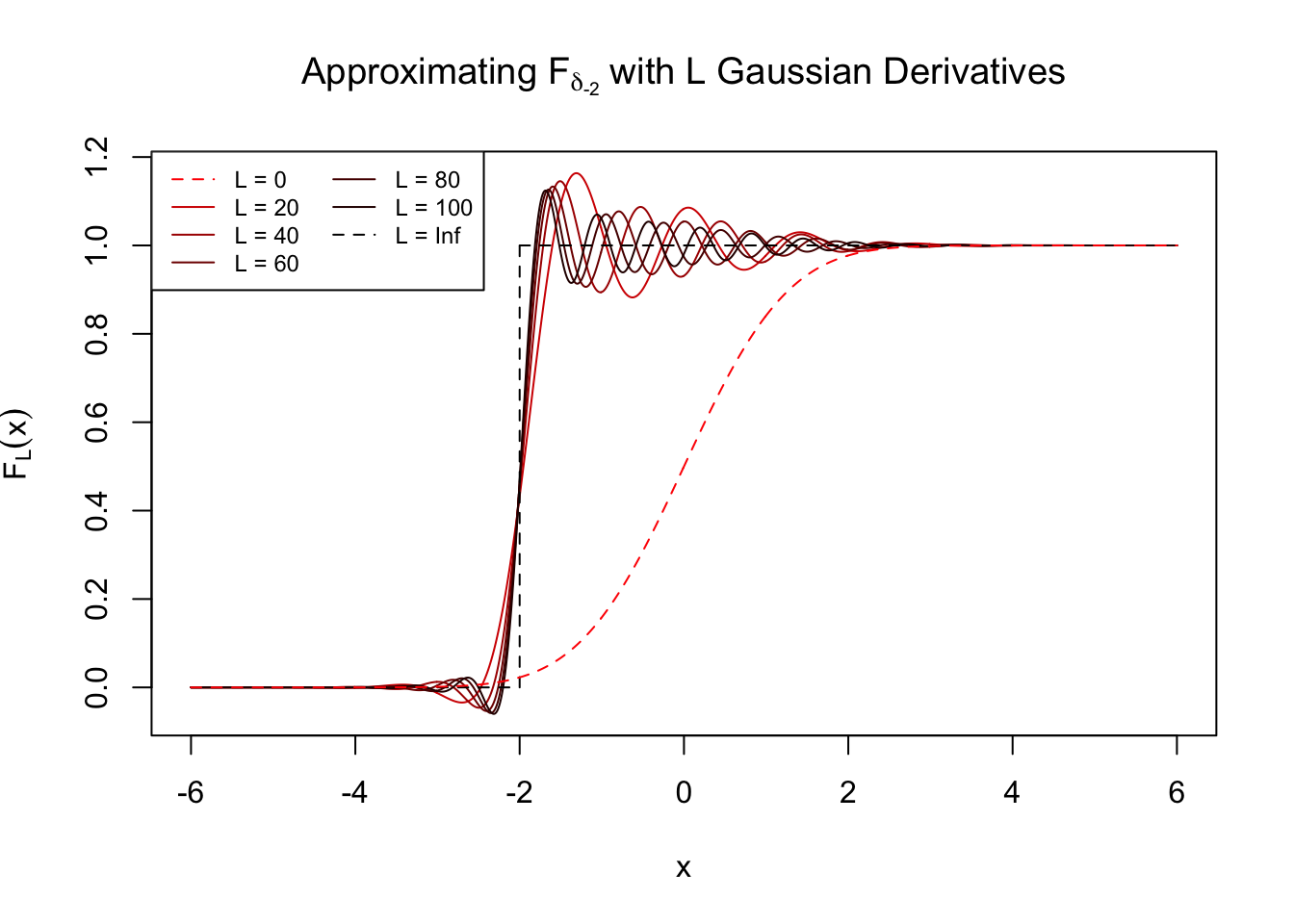
\(z = 0\)
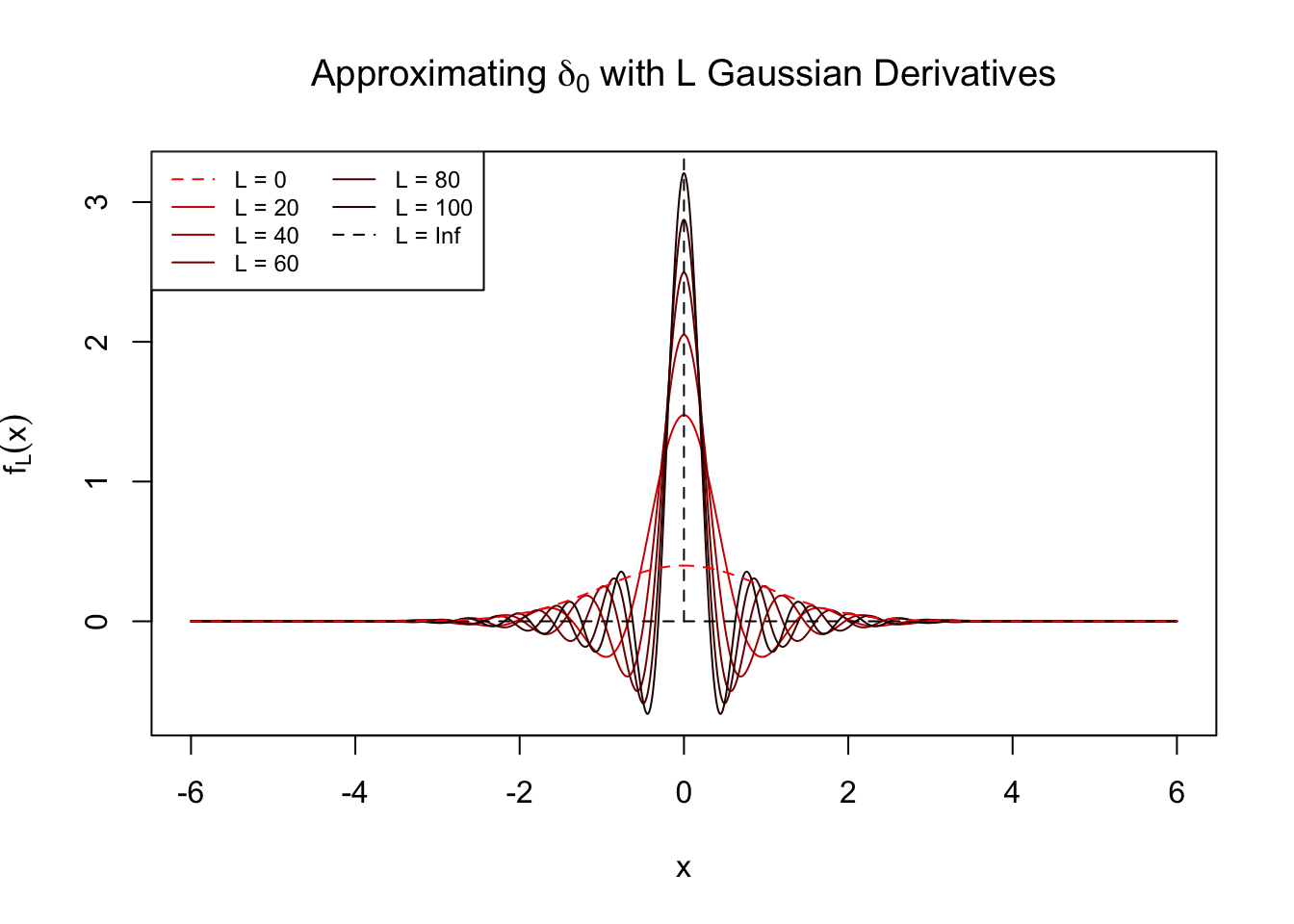
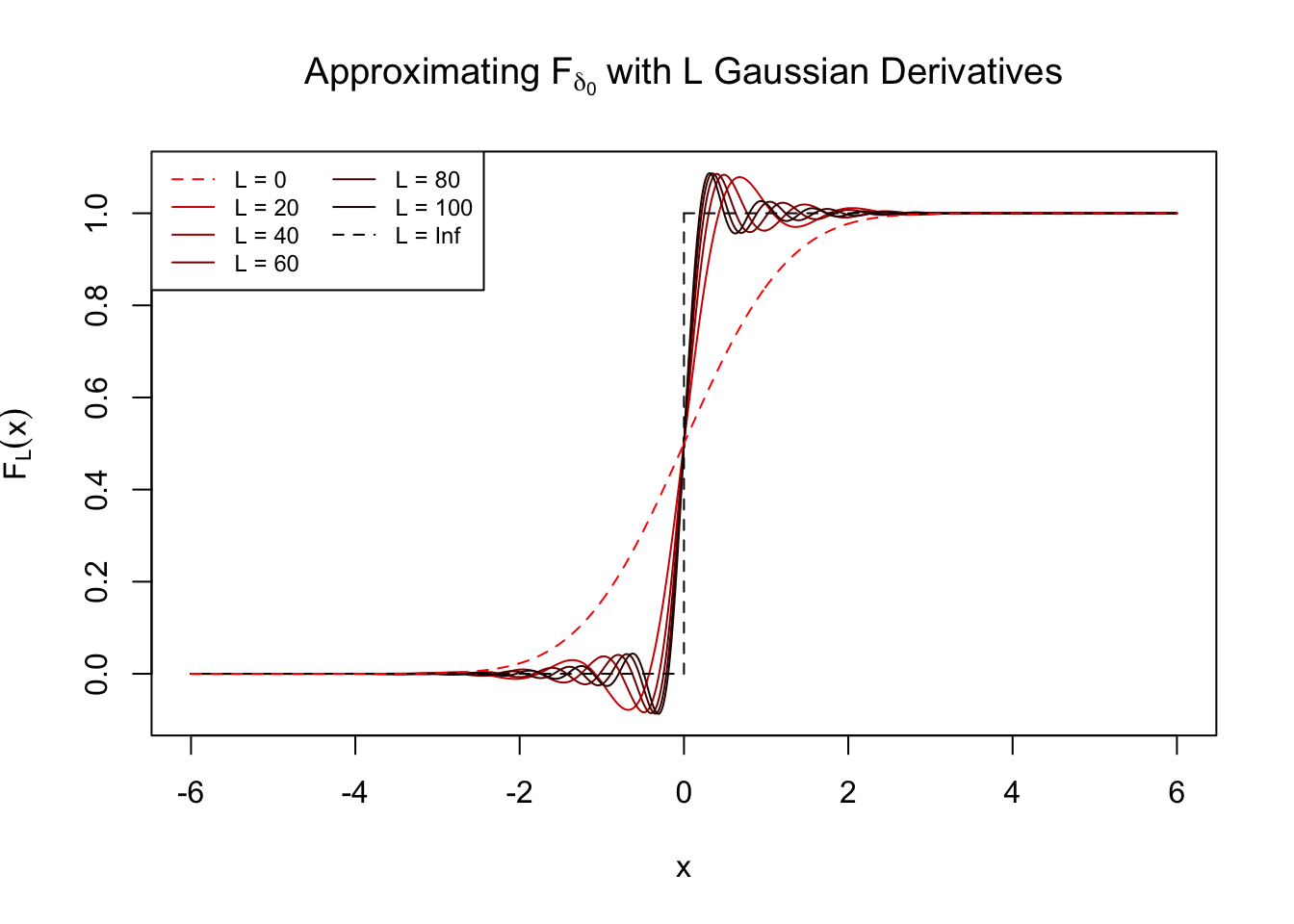
\(z = 4\)
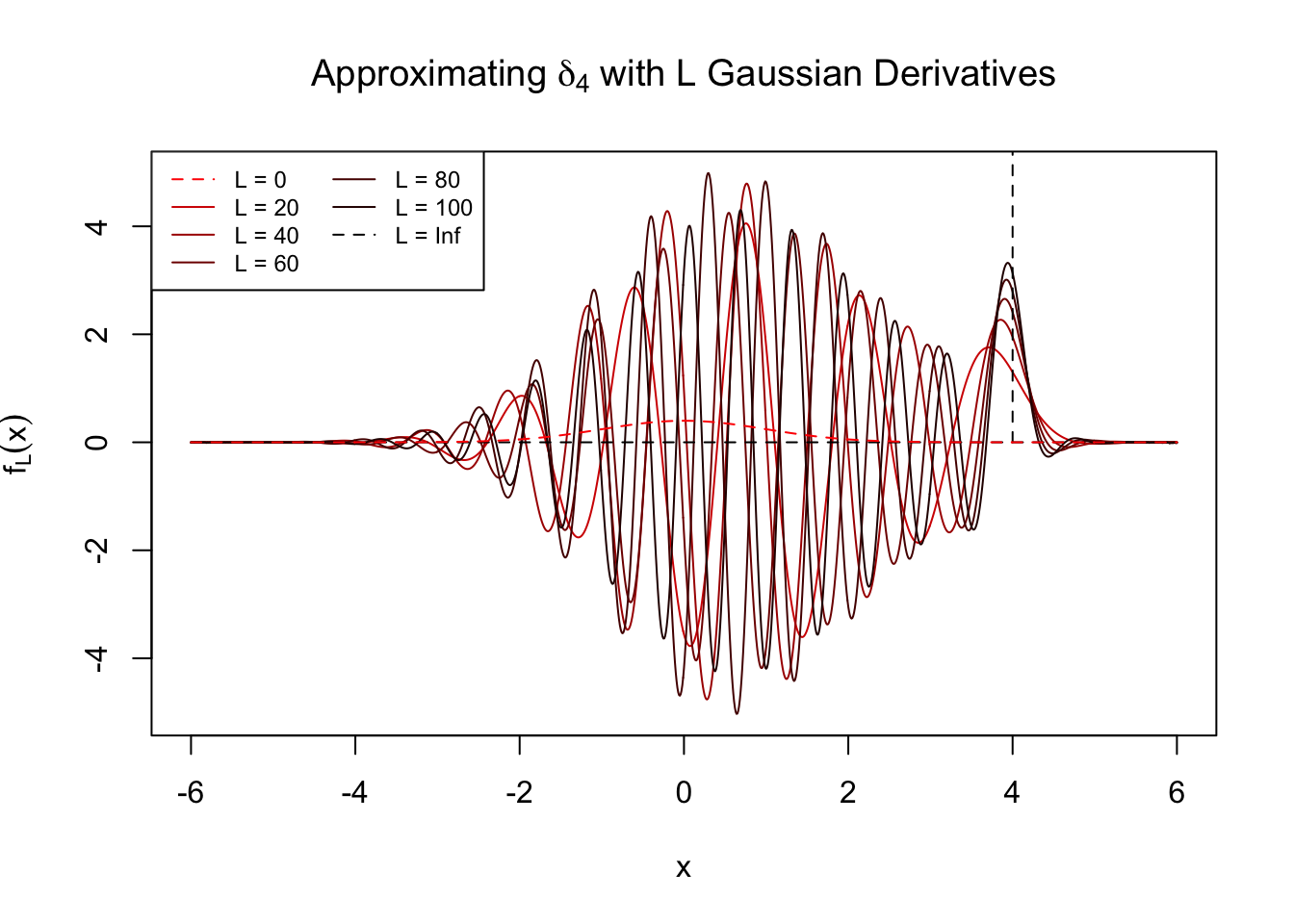
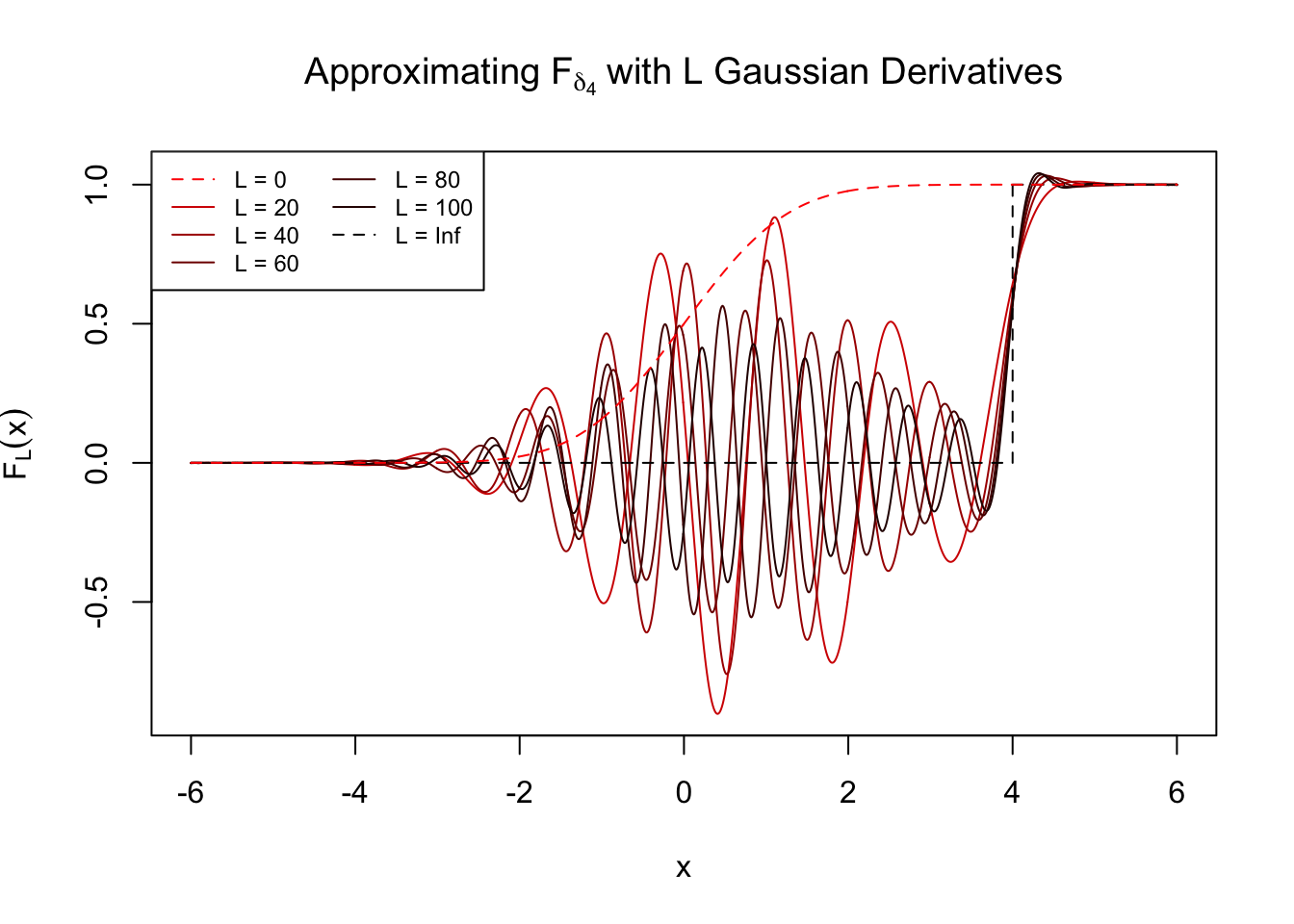
\(z = 6\)
Numerical instability.
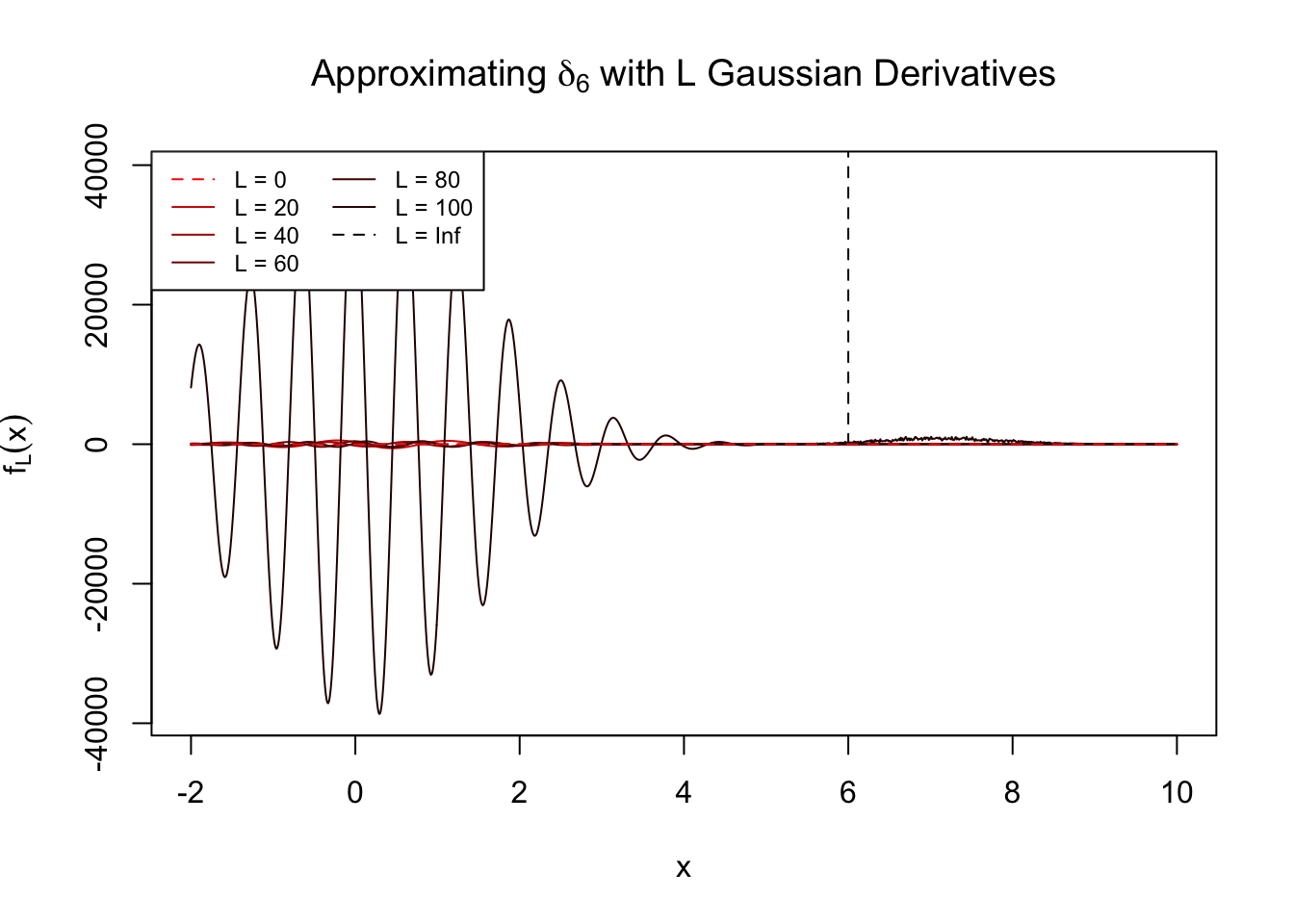
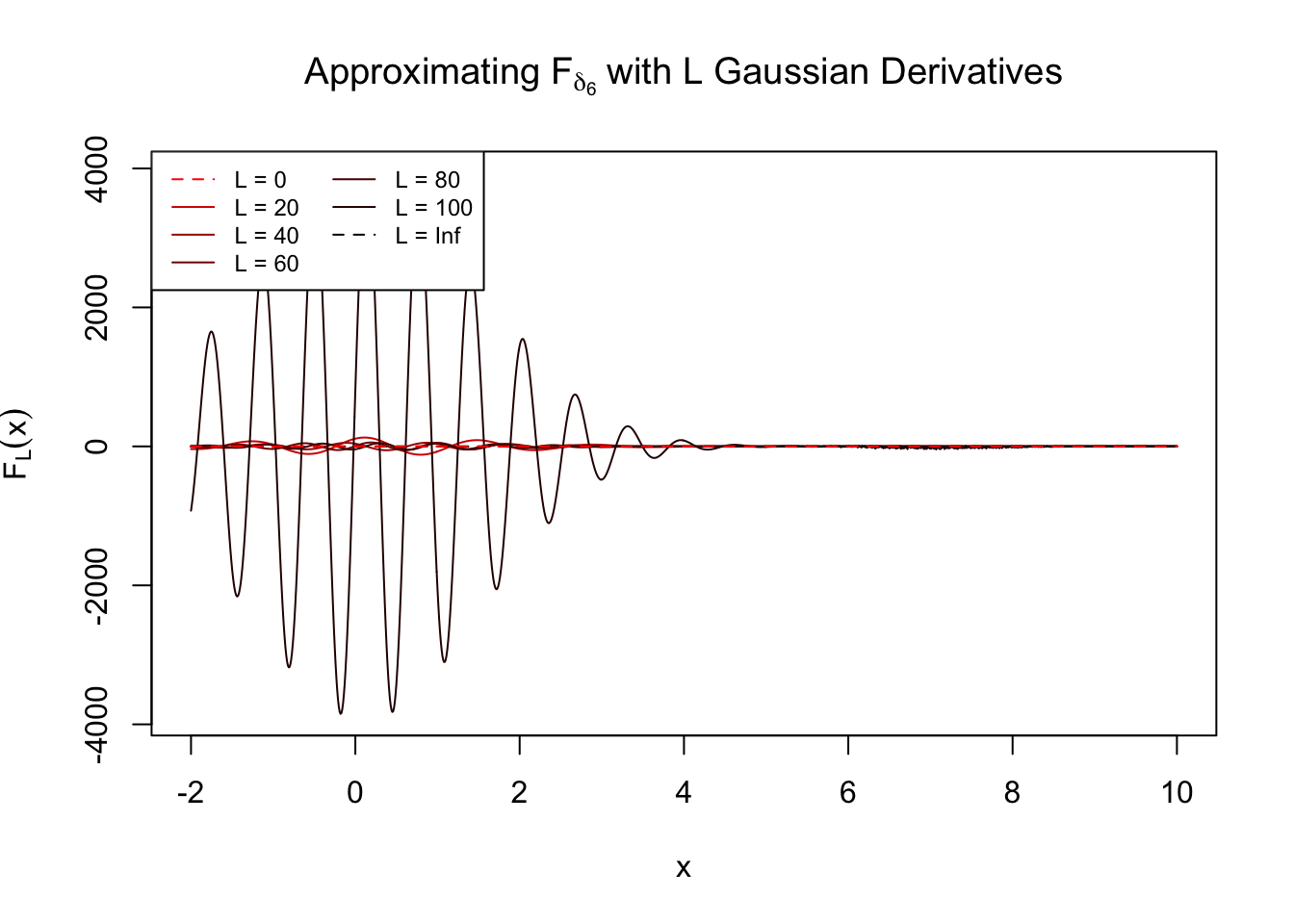
Session information
sessionInfo()R version 3.3.3 (2017-03-06)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: macOS Sierra 10.12.4
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
loaded via a namespace (and not attached):
[1] backports_1.0.5 magrittr_1.5 rprojroot_1.2 tools_3.3.3
[5] htmltools_0.3.5 yaml_2.1.14 Rcpp_0.12.10 stringi_1.1.2
[9] rmarkdown_1.3 knitr_1.15.1 git2r_0.18.0 stringr_1.2.0
[13] digest_0.6.11 evaluate_0.10 This R Markdown site was created with workflowr