Comparison with Knockoff: \(\Sigma_X\) is Toeplitz
Lei Sun
2017-01-18
Last updated: 2018-01-30
Code version: 5442ab8
Introduction
Applying CASH to linear regression variable selection, compared with other popular methods including BH, Knockoff.
Simulation Setting
The simulation setting is very similar to what’s used in Knockoff’s vignette. The only notable difference is that the non-zero signals are normally distributed centered at zero, rather than constant.
Data are simulated by \[ y_n = X_{n \times p}\beta_p + e_n \] where \[ \begin{array}{c} n = 2000 \\ p = 1000 \\ e_n \sim N(0, 1) \\ \beta \sim \eta\delta_0 + (1 - \eta)N(0, \sigma /\sqrt{n}) \end{array} \] Each row of \(X\) is generated independently from a \(N(0, \Sigma_\rho)\) distribution, where \(\left(\Sigma_\rho\right)_{j, k} = \rho^{|j - k|}\), a Toplitz matrix.
Every method selects the variables with respect to a nominal false discovery rate \(q = 0.1\).
In simulations, we are changing the values of the sparsity level \(\eta\), the signal strength \(\sigma\), the feature correlation \(\rho\).
Methods
BH: First run multiple linear regression, then apply BH to obtained \(p\)-values.
qvalue: First run multiple linear regression, then apply
qvalue::qvalueto obtained \(p\)-values.Knockoff: Directly apply
knockoff::knockoffon \(X\), \(y\).ASH: First run multiple linear regression, then apply
ashr::ashon obtained \(\hat\beta\) and \(\hat{\text{se}}\left(\hat \beta\right)\), using normal mixture and normal likelihood.CASH: First run multiple linear regression, then apply
cashon obtained \(\hat\beta\) and \(\hat{\text{se}}\left(\hat \beta\right)\), using normal mixture and normal likelihood, with default penalty on Gaussian derivative coefficients.CASH+: CASH with perfect knowledge, using real noise level \(\text{se}\left(\hat{\beta}\right)\).
Observations
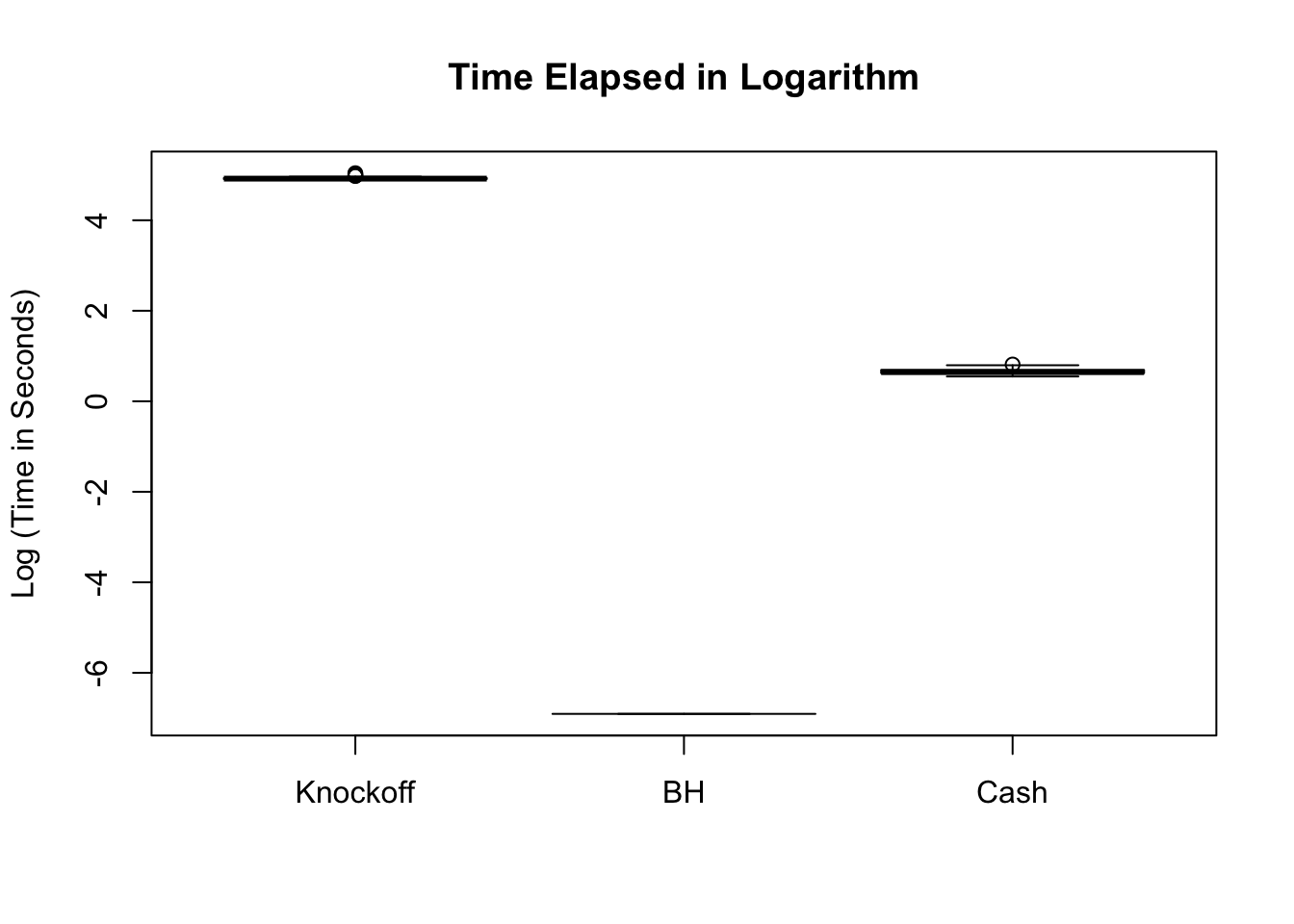
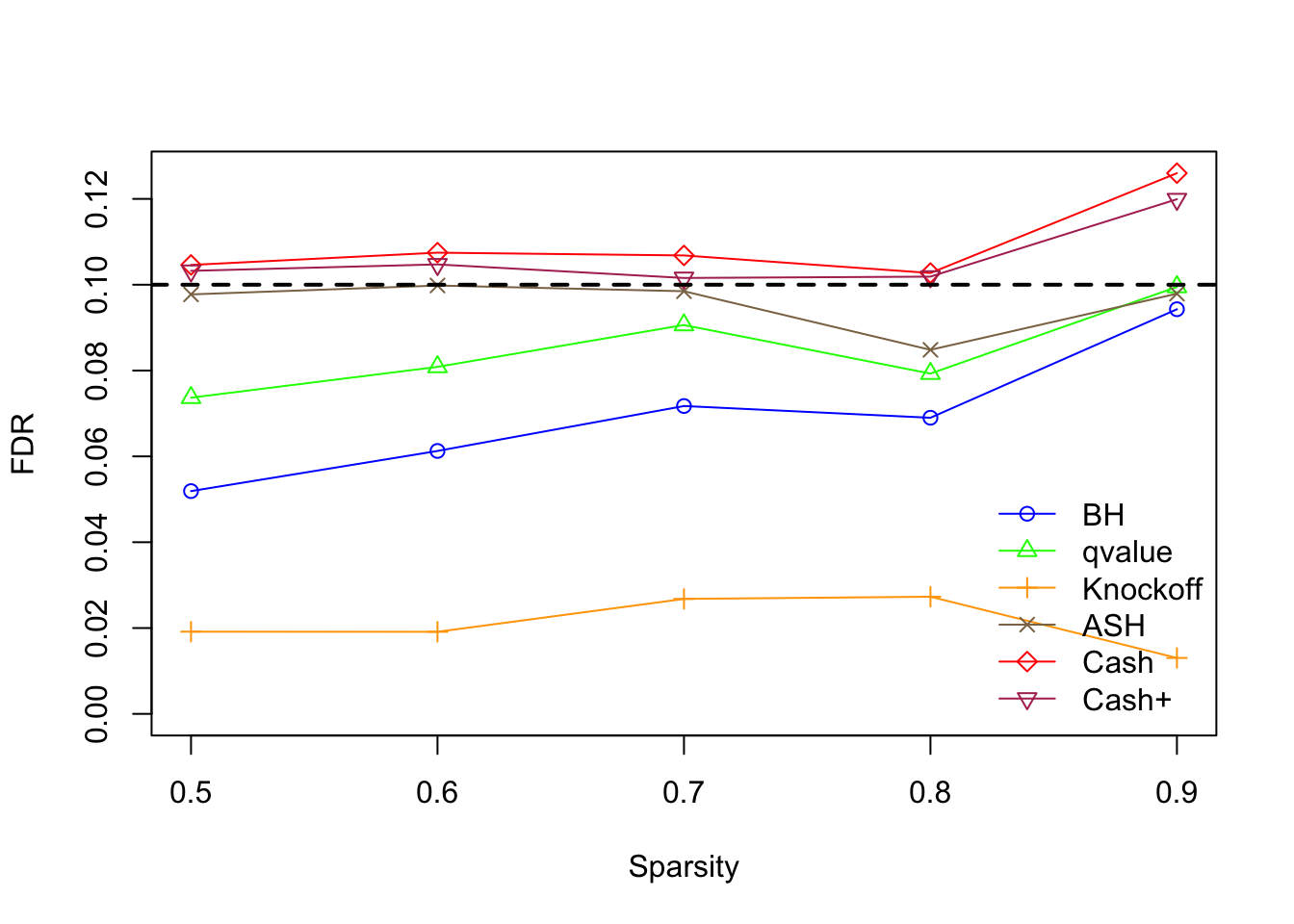
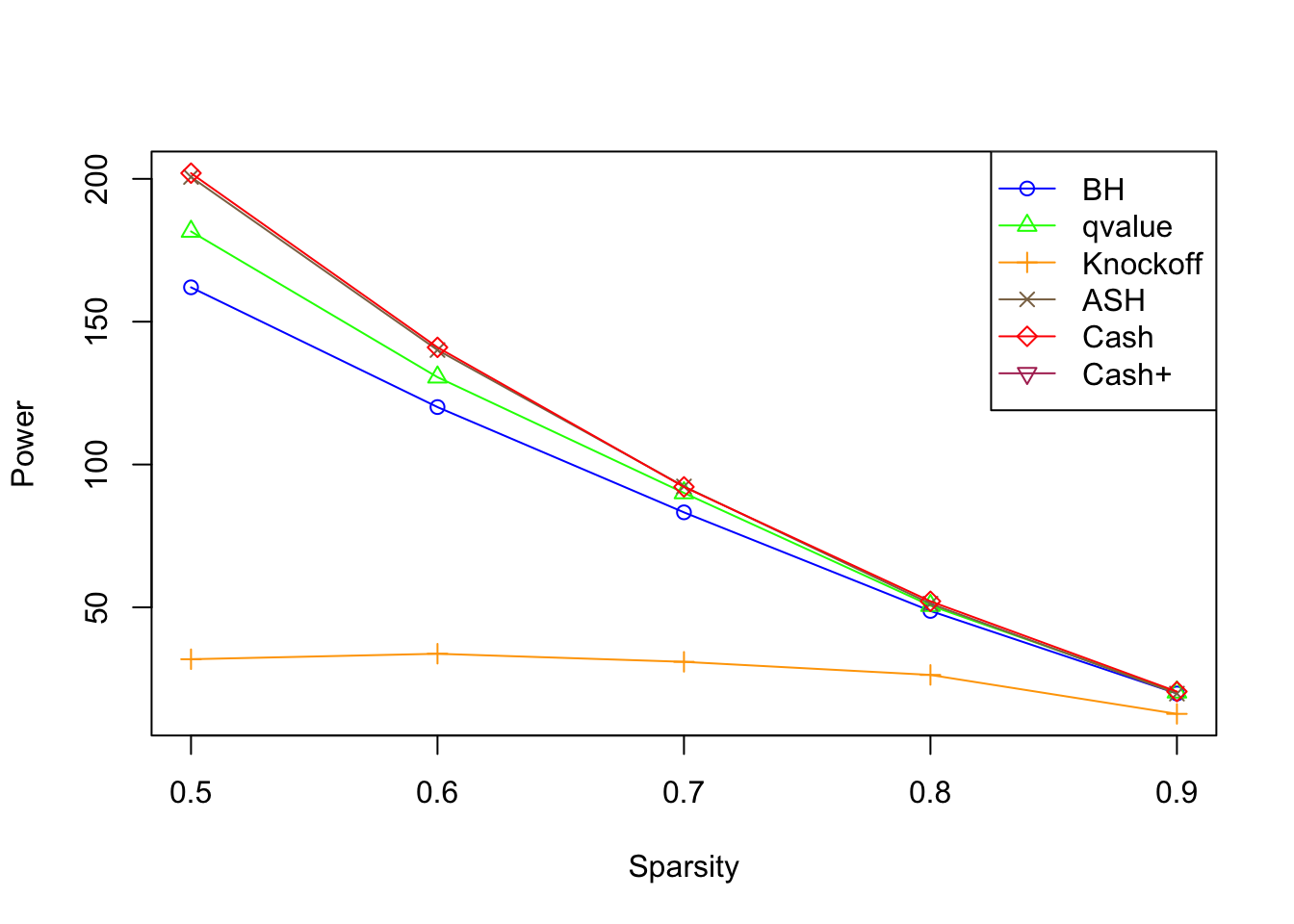
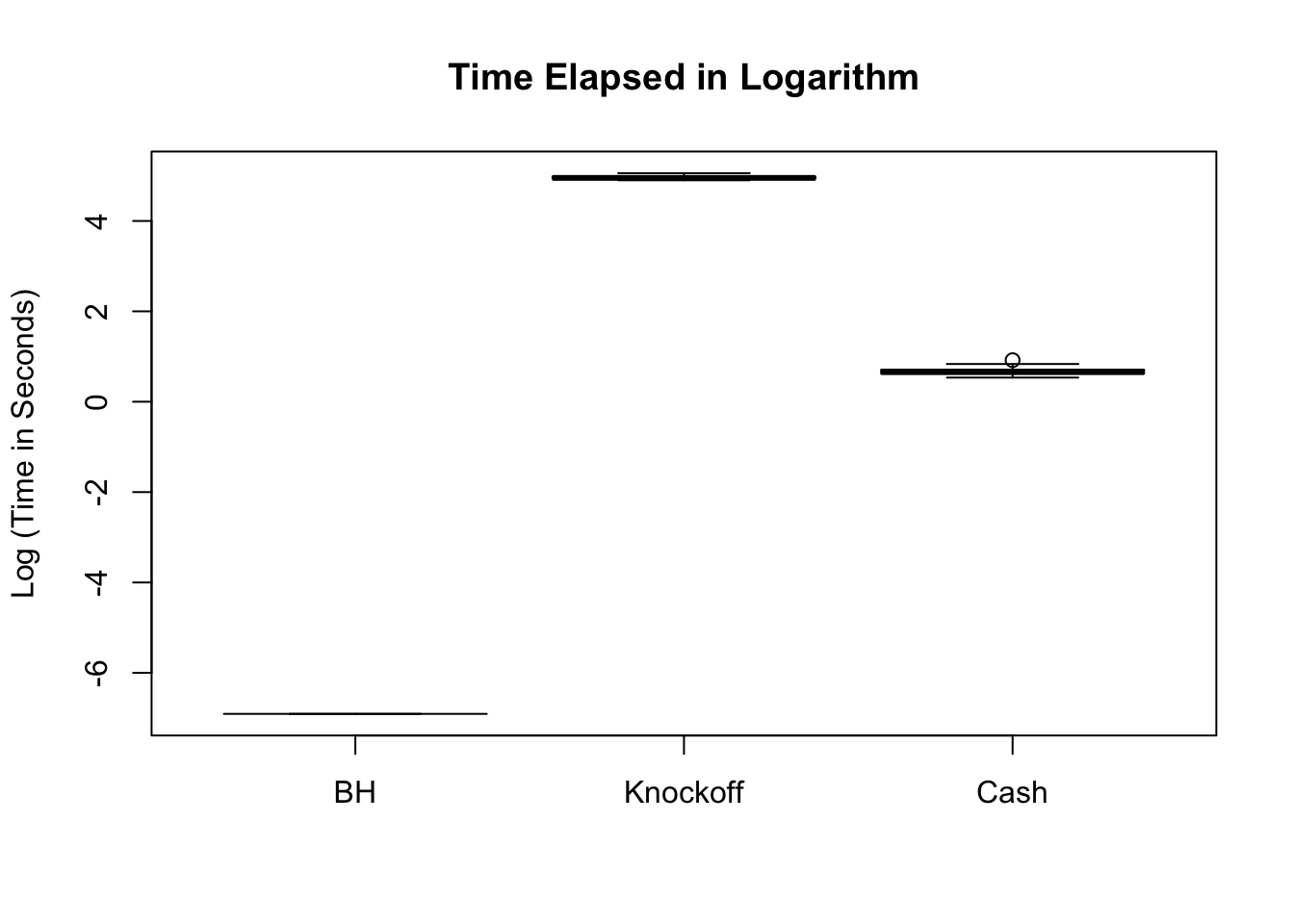
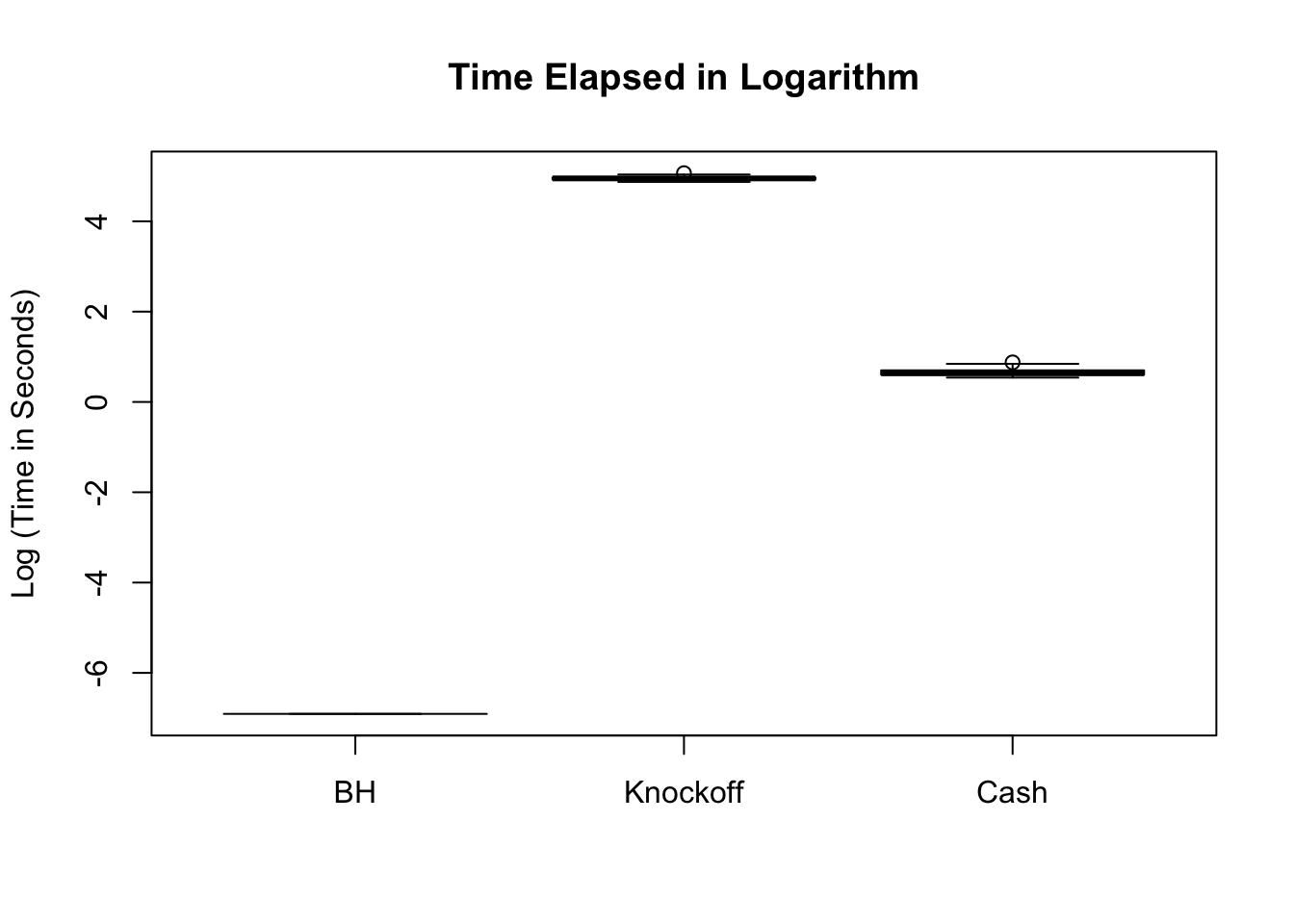
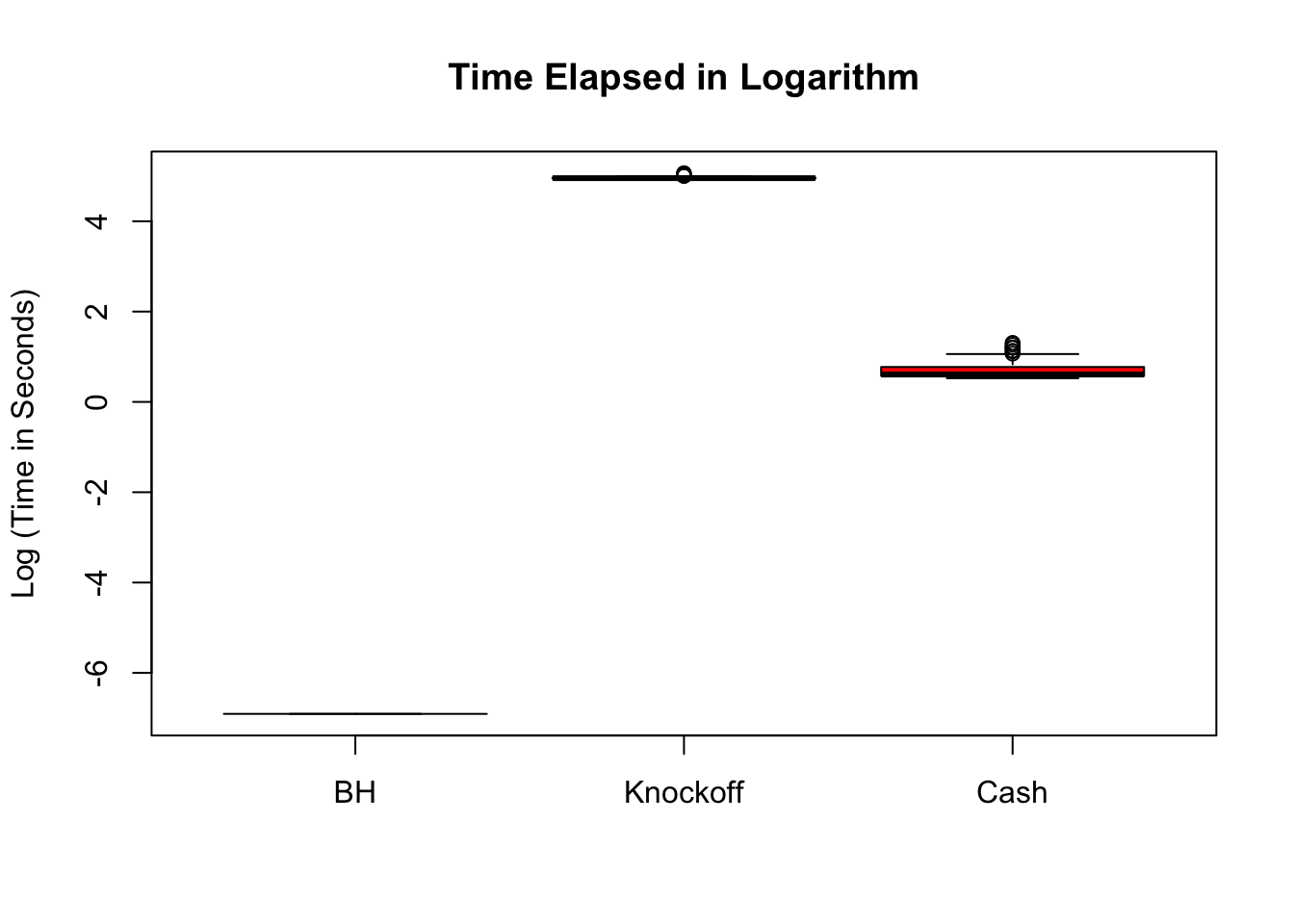
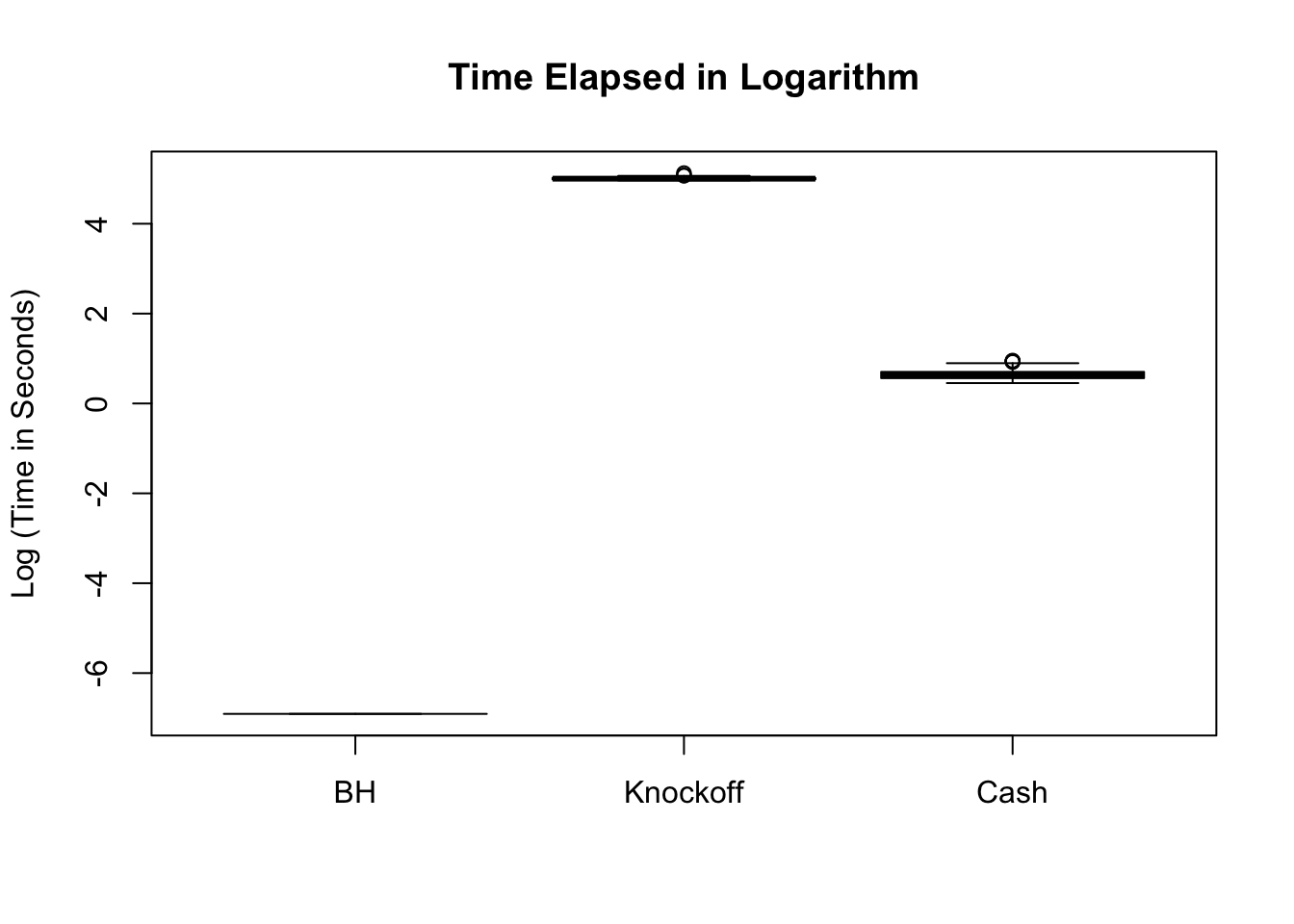
BH is very robust, very fast.
Knockoff is way too slow and way too conservative with signals being unimodal at zero. Perhaps it needs strong signals distinctly different from the “bulk.” Unimodal setting is really adversary to this method.
CASHworks fine, but not better than the basicASH.
\(\eta = 0.9\), \(\sigma = 5\), \(\rho = 0.5\)
No id variables; using all as measure variables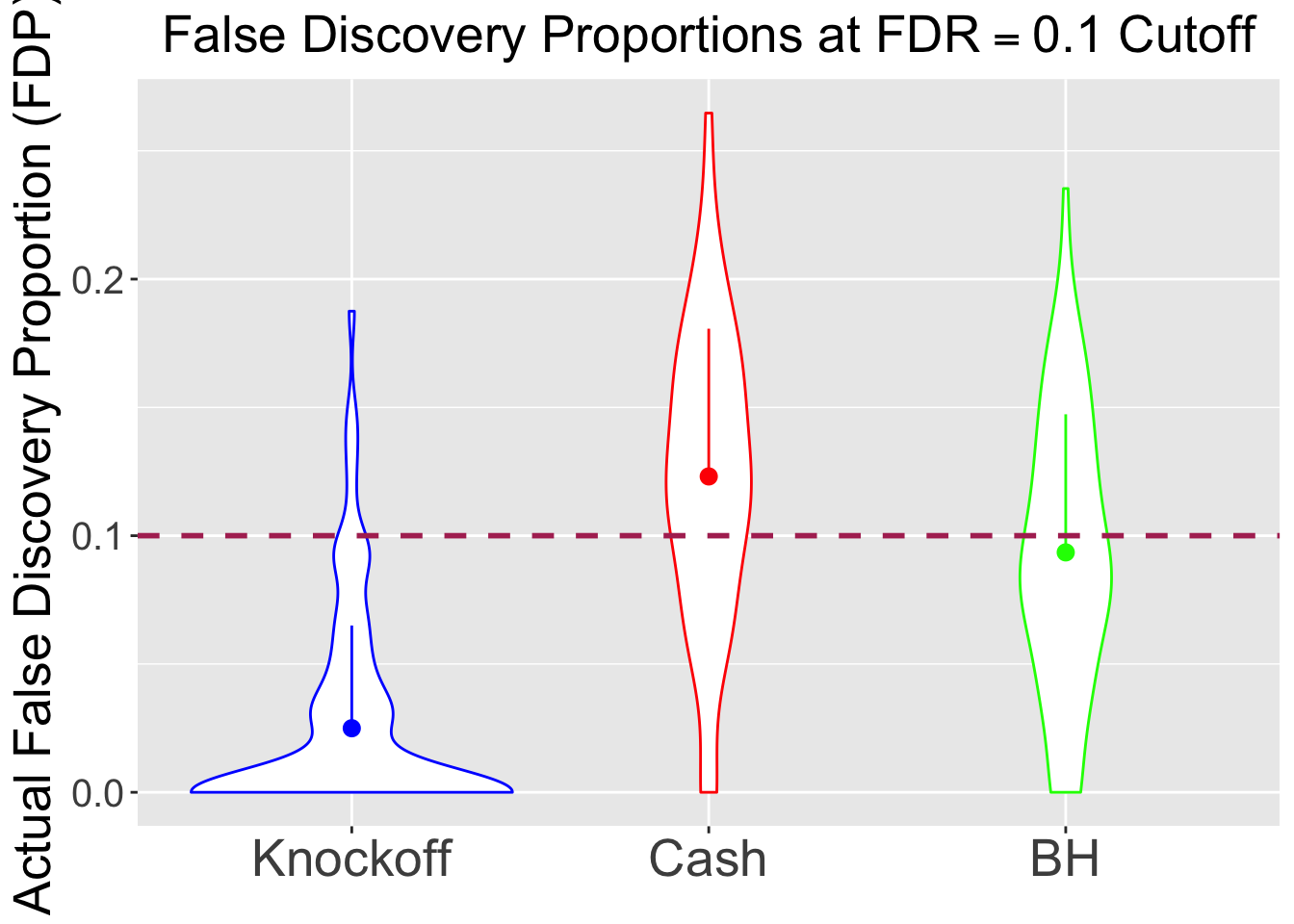
No id variables; using all as measure variables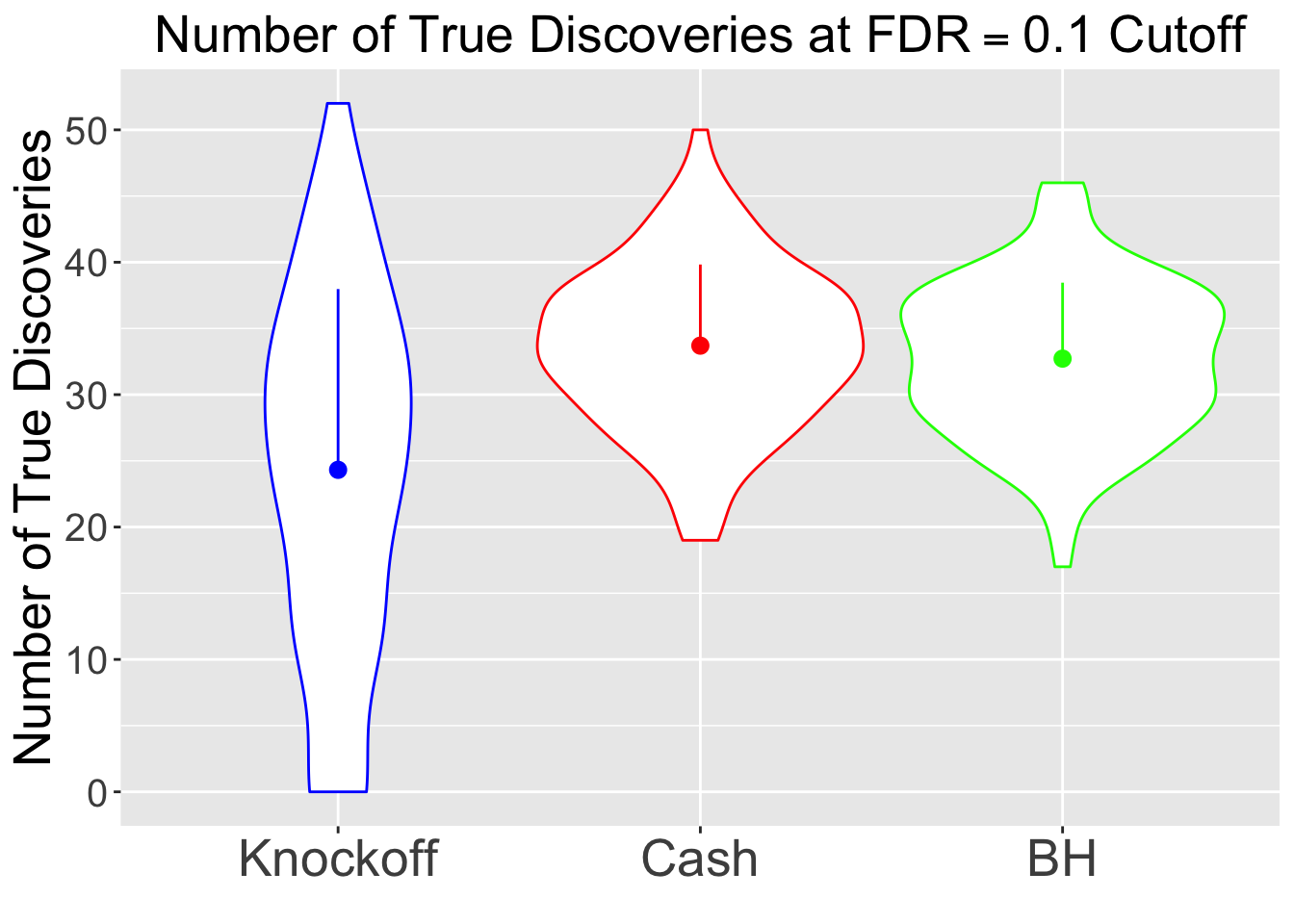
Warning in bplt(at[i], wid = width[i], stats = z$stats[, i], out = z$out[z
$group == : Outlier (-Inf) in boxplot 3 is not drawn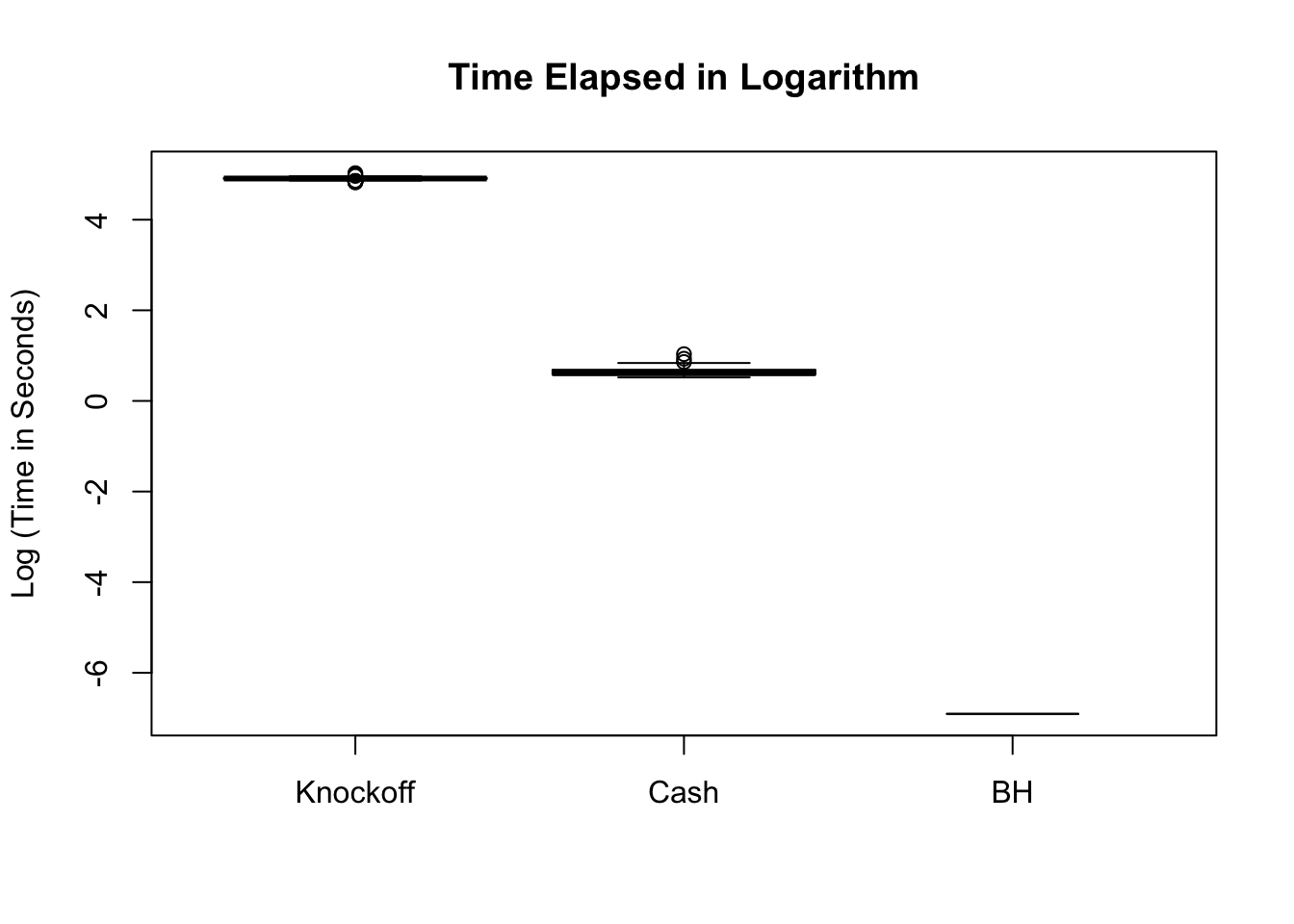
\(\eta = 0.8\), \(\sigma = 4\), \(\rho = 0.5\)
No id variables; using all as measure variables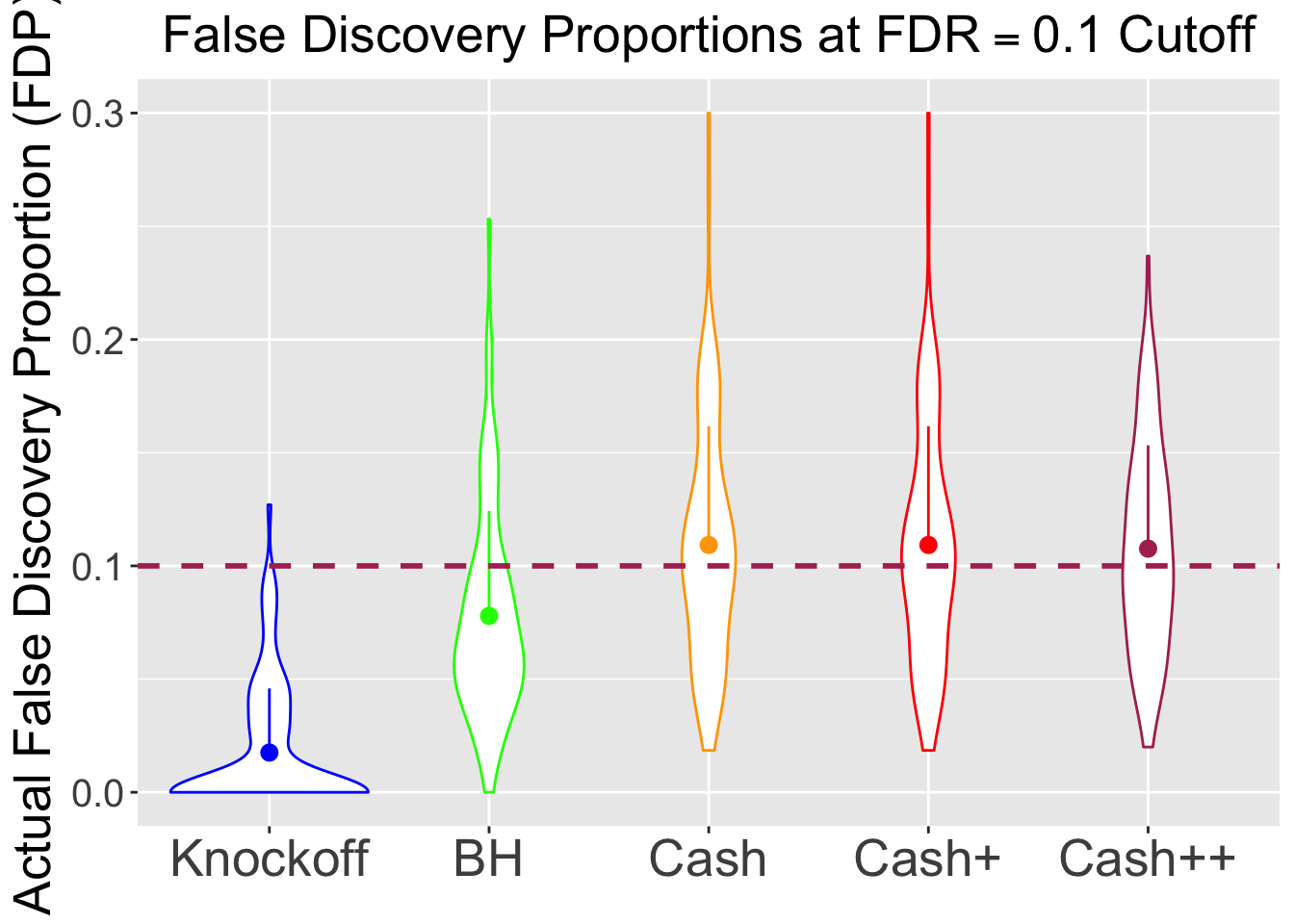
No id variables; using all as measure variables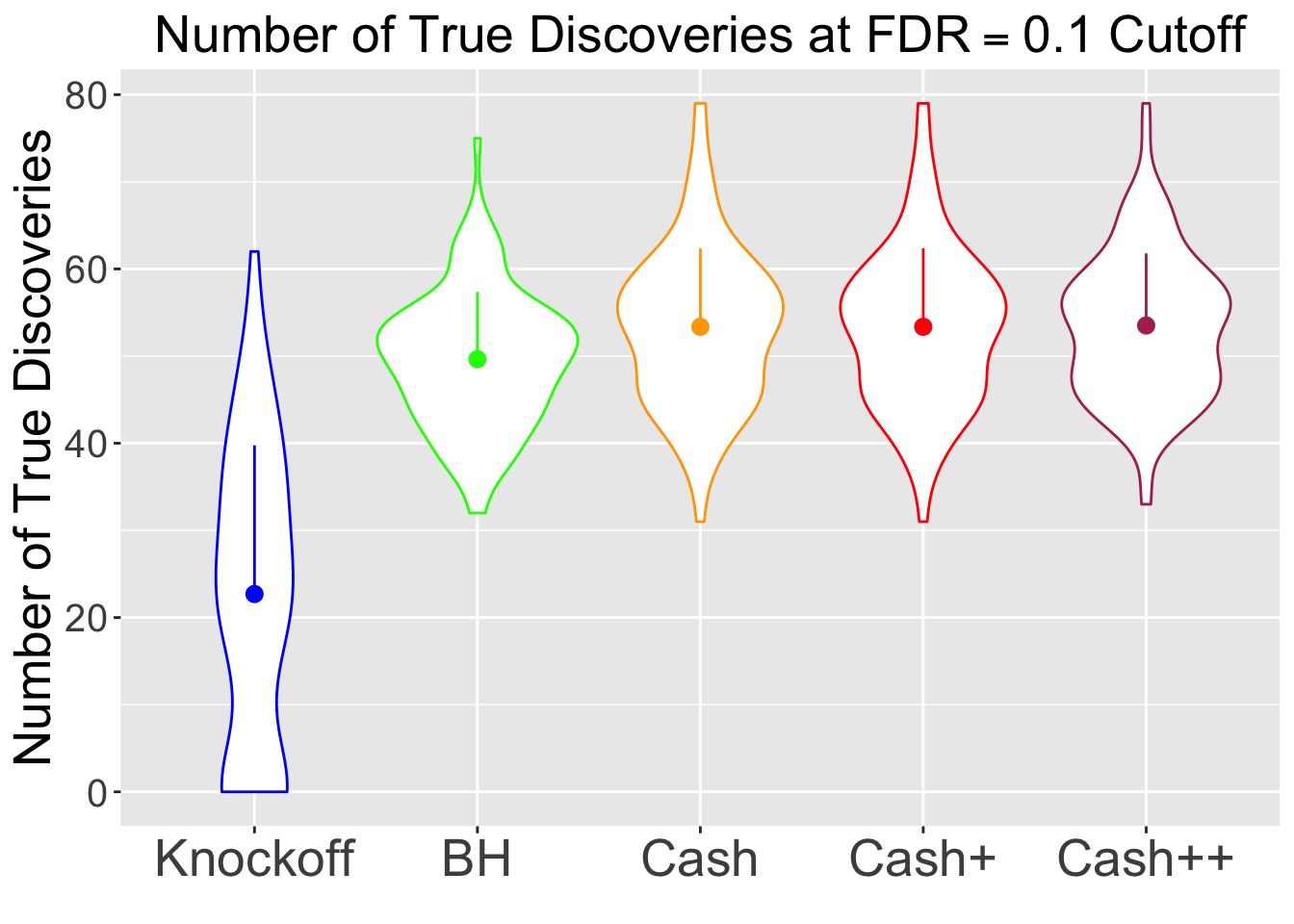
Warning in bplt(at[i], wid = width[i], stats = z$stats[, i], out = z$out[z
$group == : Outlier (-Inf) in boxplot 2 is not drawn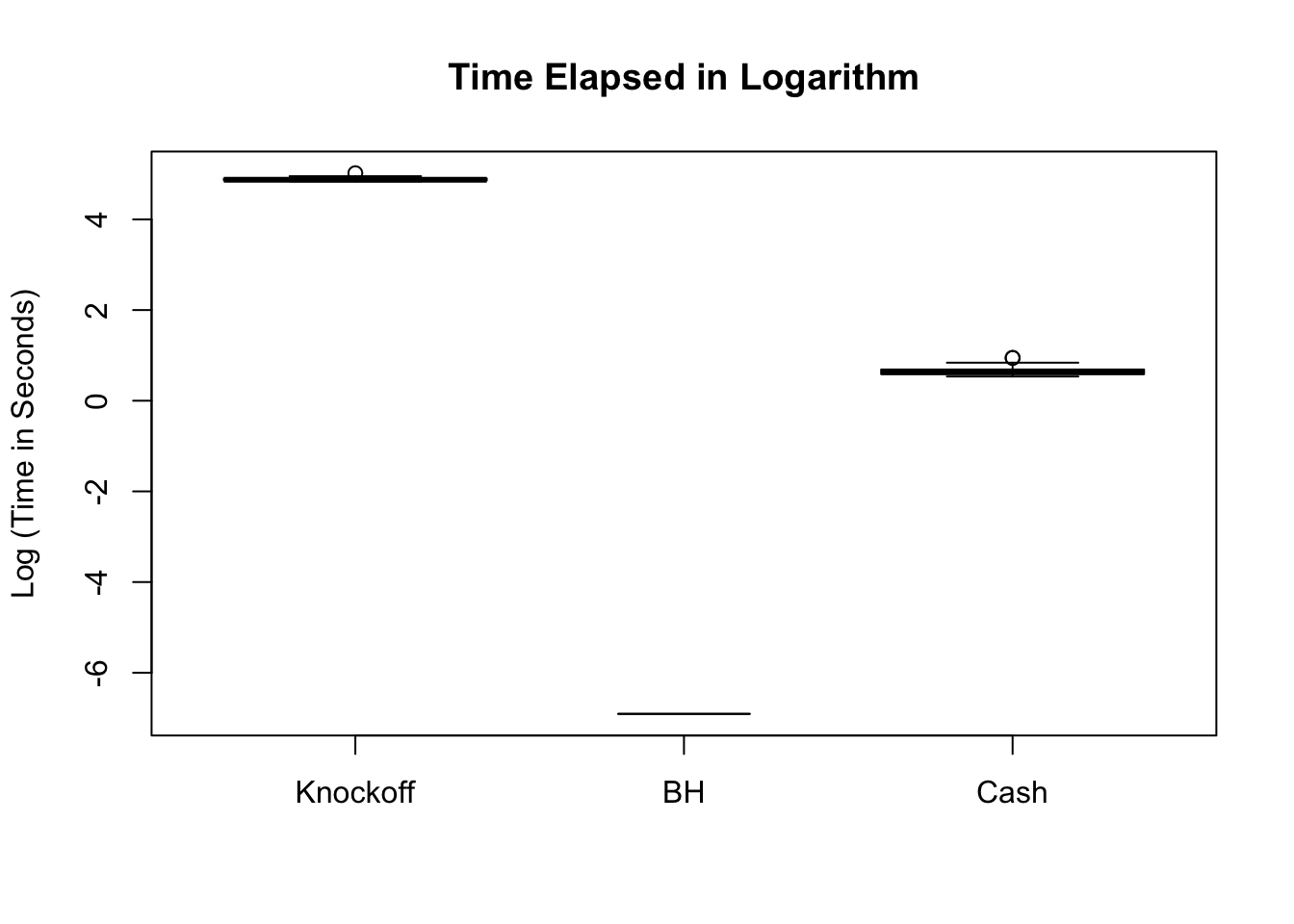
\(\eta = 0.5\), \(\sigma = 4\), \(\rho = 0.5\)
No id variables; using all as measure variables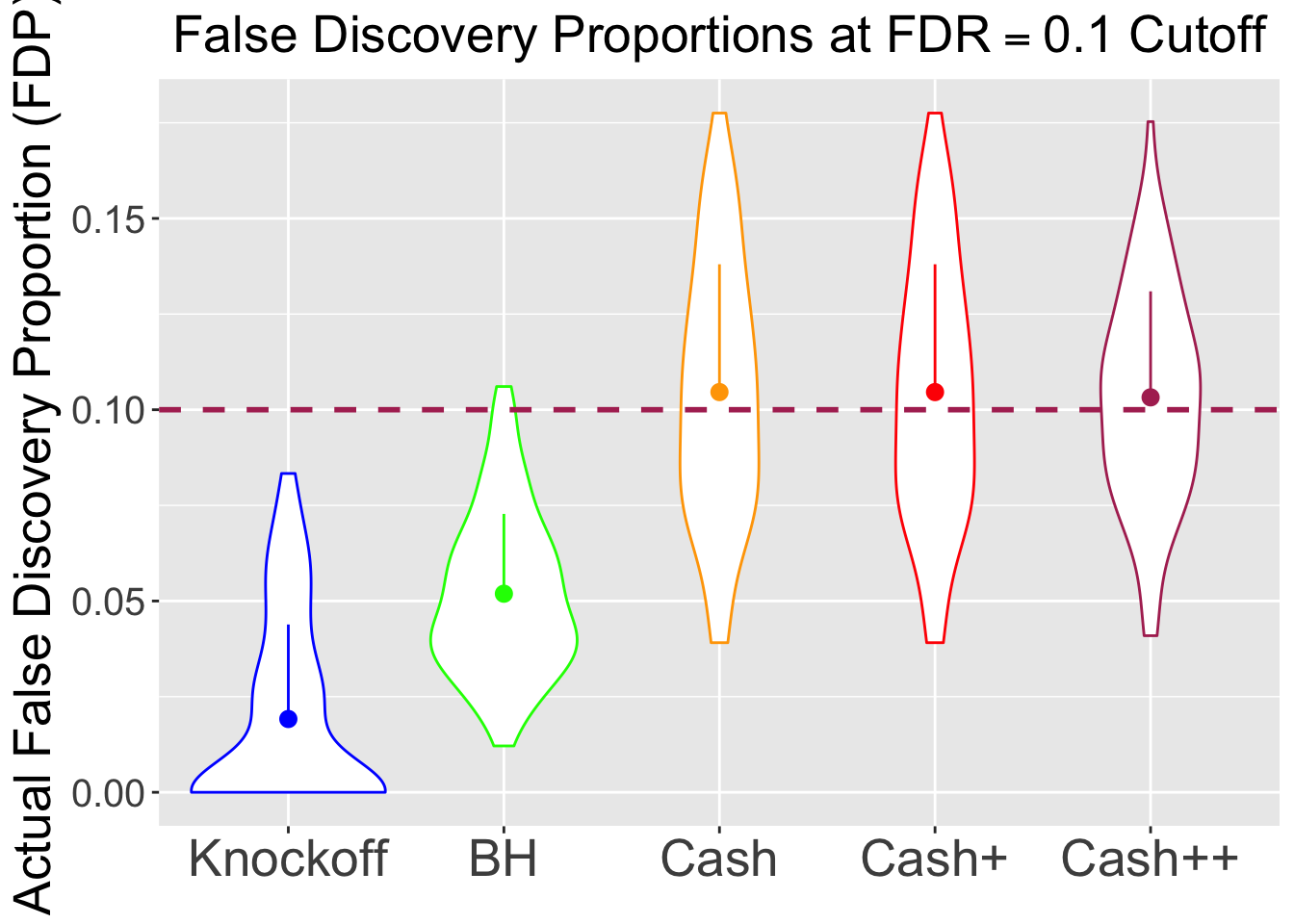
No id variables; using all as measure variables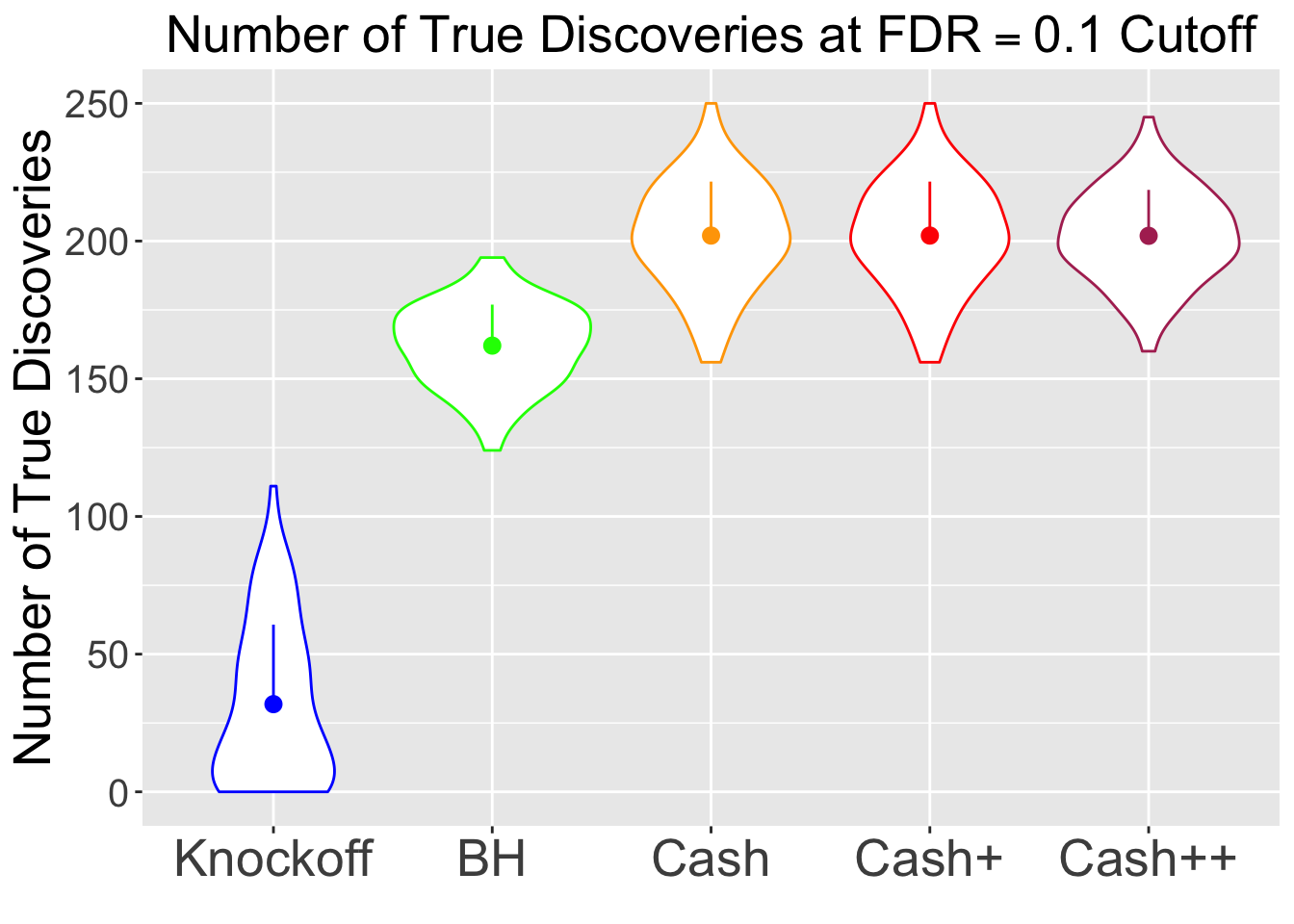
\(\eta \in \left\{0.5, 0.6, 0.7, 0.8, 0.9\right\}\), \(\sigma = 4\), \(\rho = 0.5\)
Overall across all sparsity
\(\eta = 0.5\), \(\sigma = 4\), \(\rho = 0.5\)
No id variables; using all as measure variables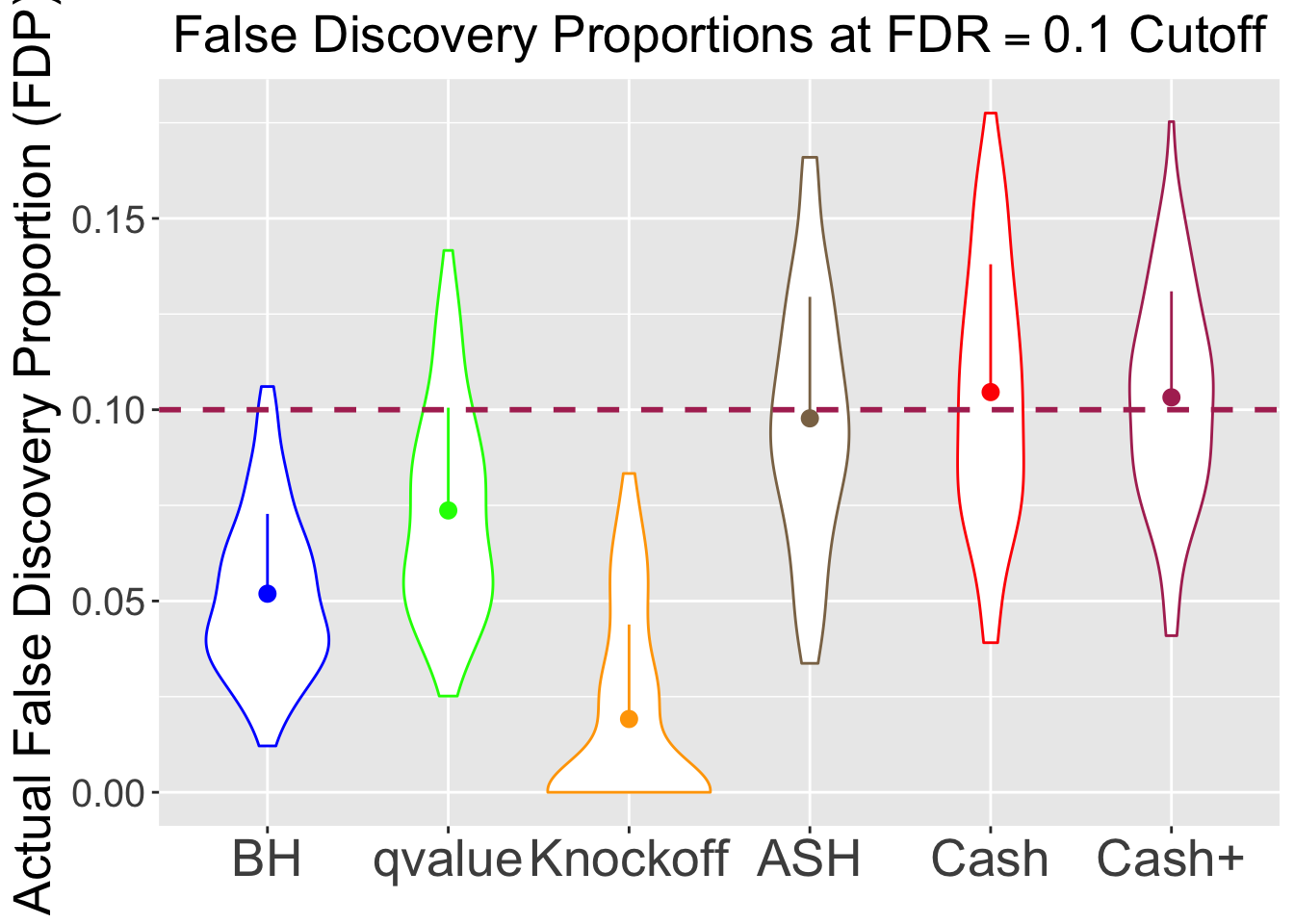
No id variables; using all as measure variables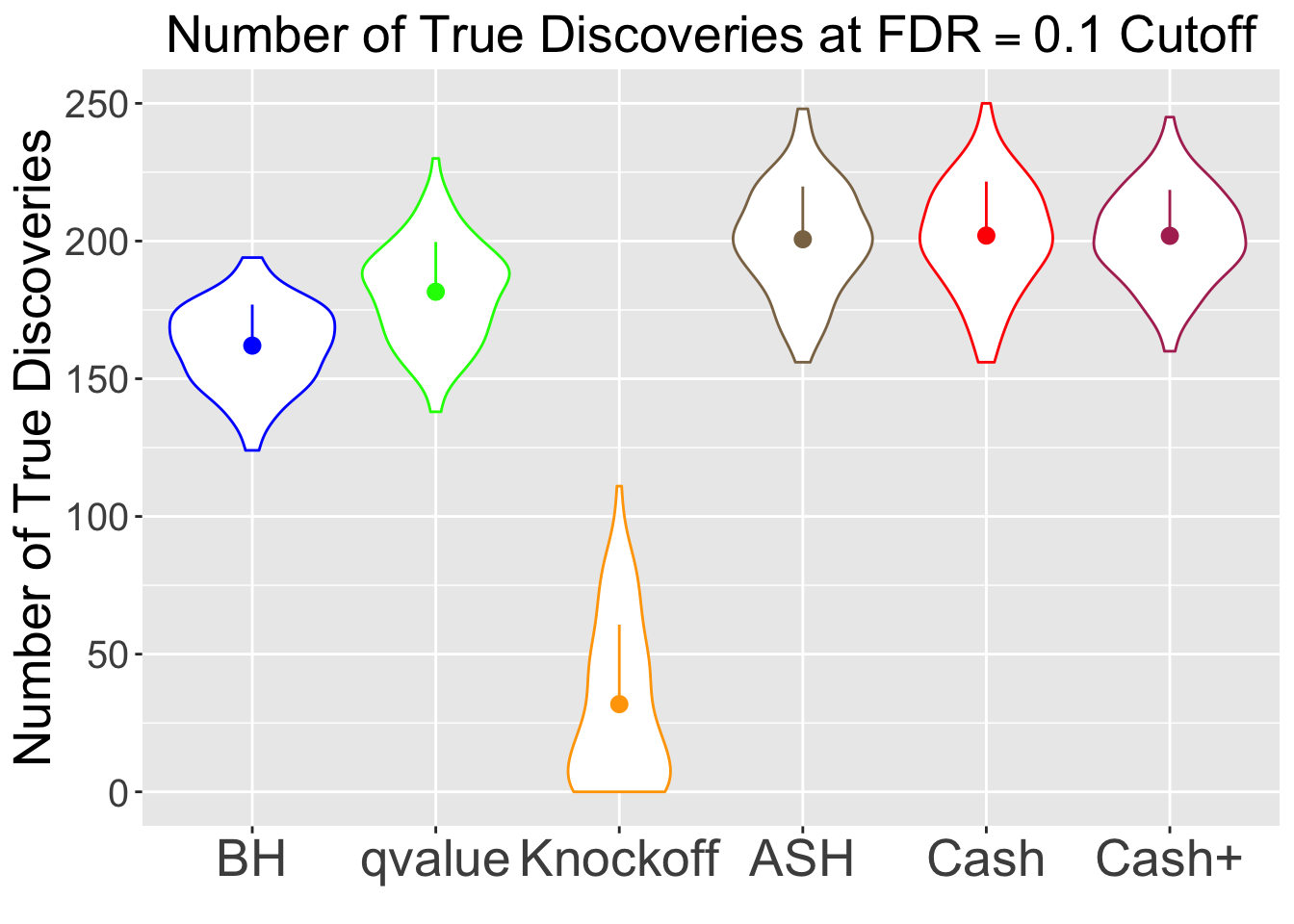
\(\eta = 0.9\), \(\sigma = 4\), \(\rho = 0.5\)
No id variables; using all as measure variables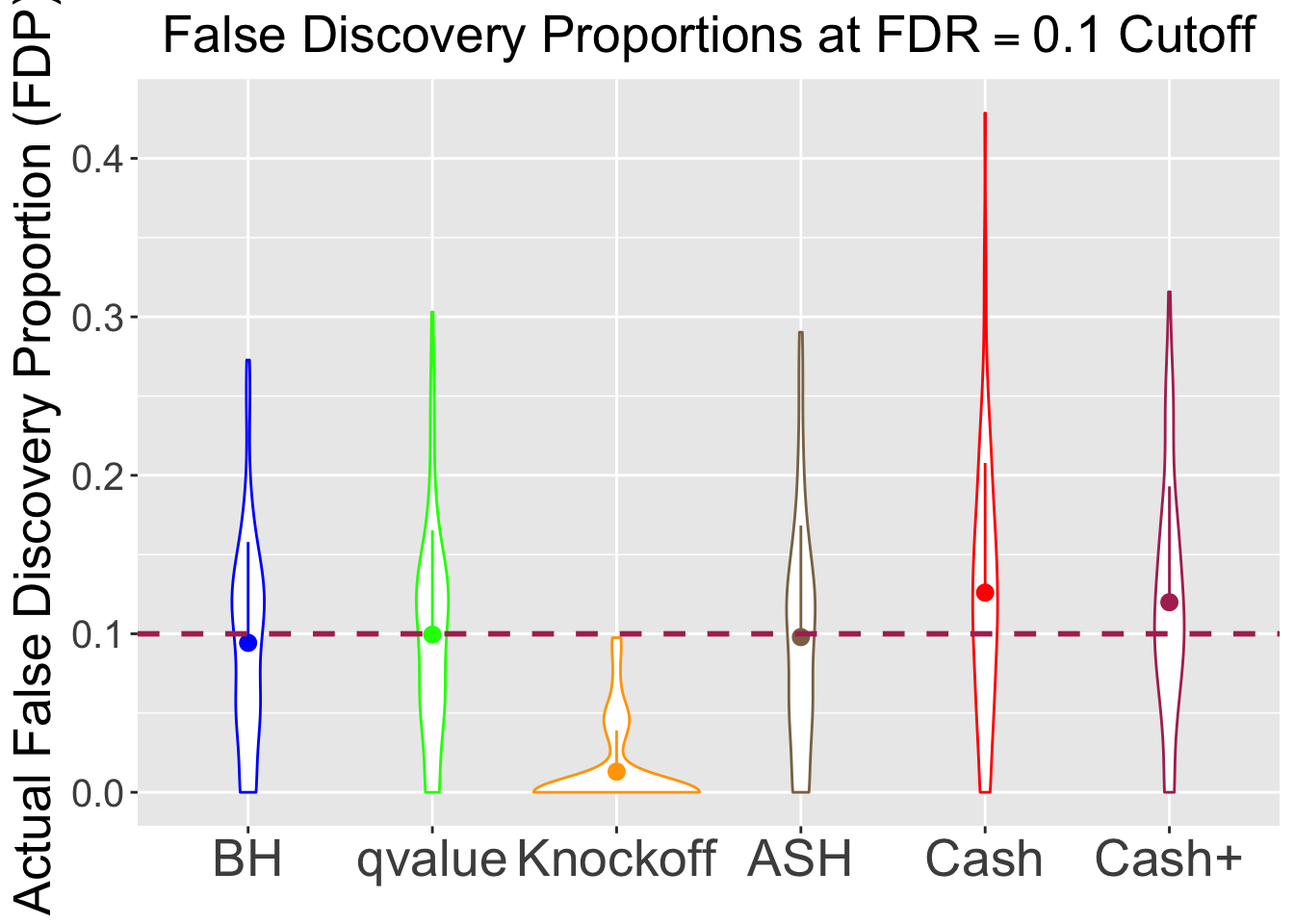
No id variables; using all as measure variables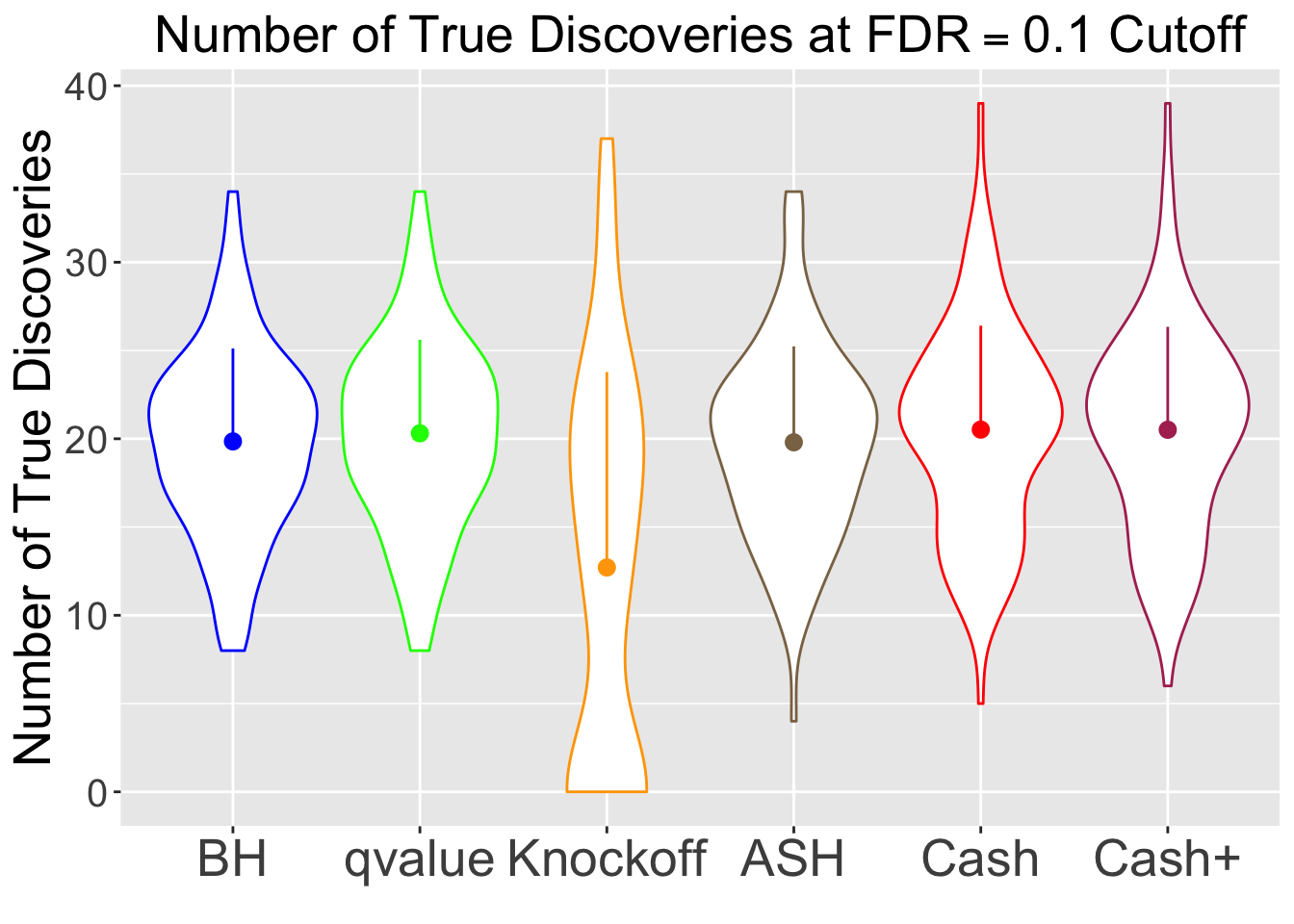
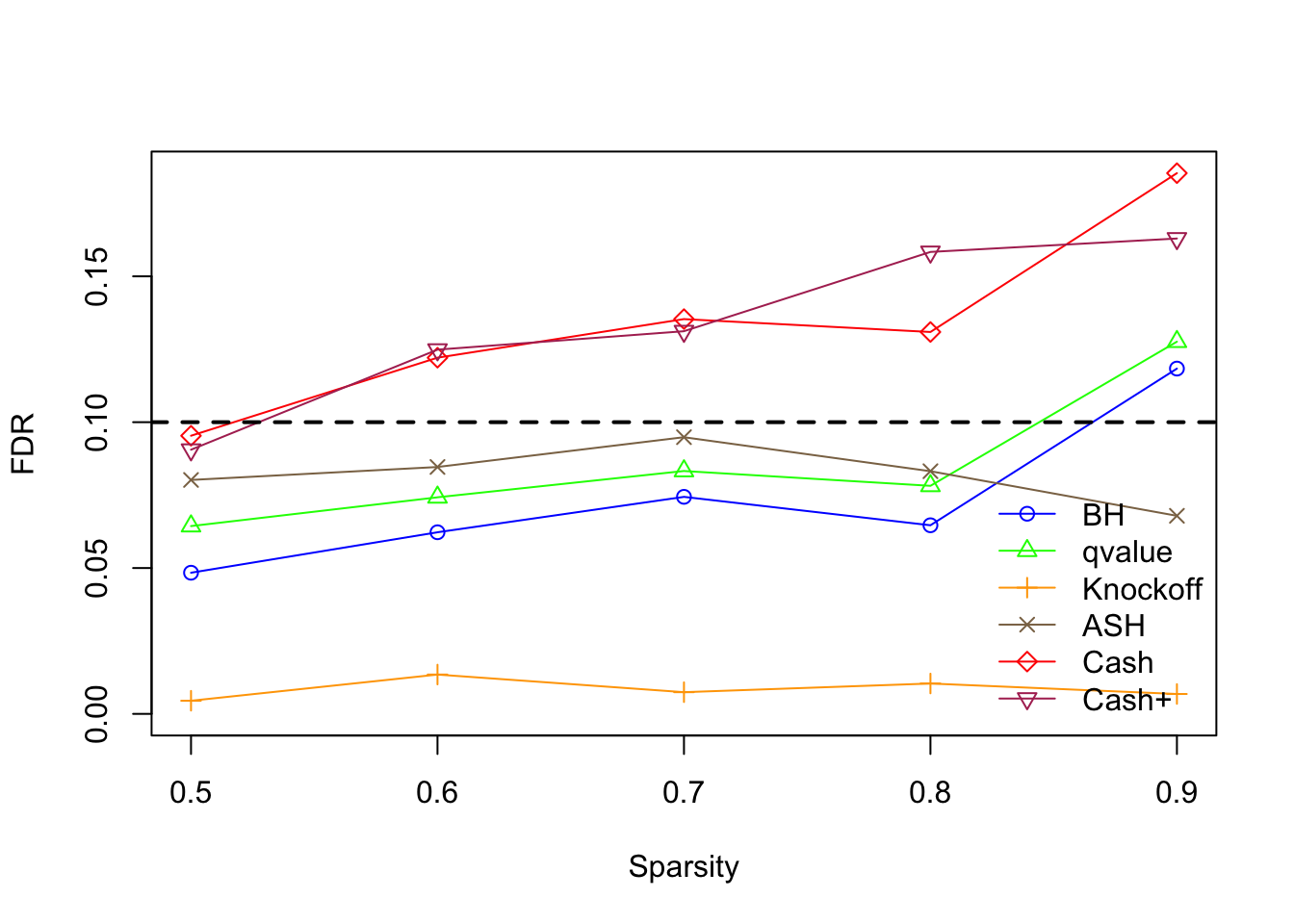
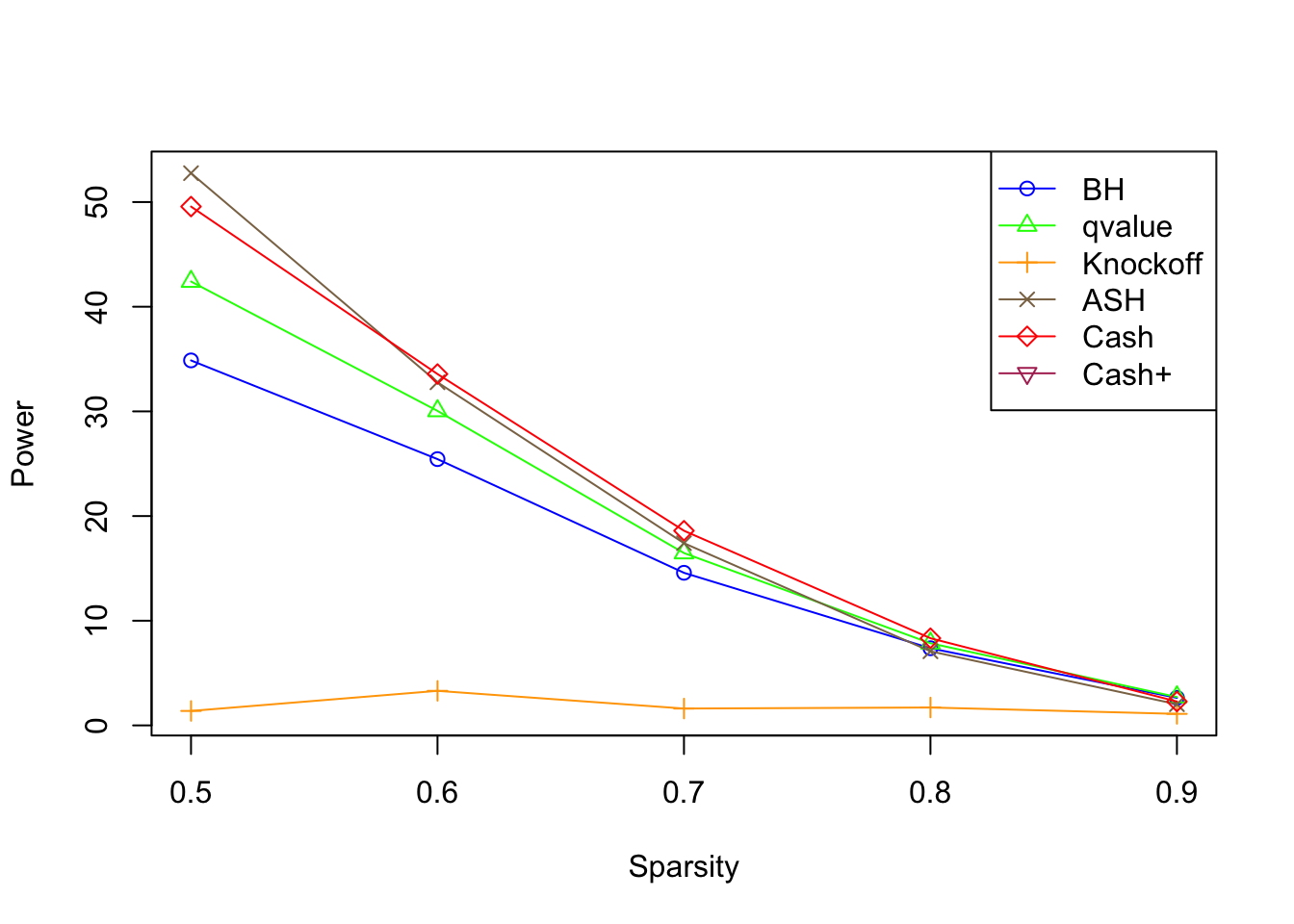
\(\eta \in \left\{0.5, 0.6, 0.7, 0.8, 0.9\right\}\), \(\sigma = 3\), \(\rho = 0.7\)
Overall across all sparsity
\(\eta = 0.5\), \(\sigma = 3\), \(\rho = 0.7\)
No id variables; using all as measure variables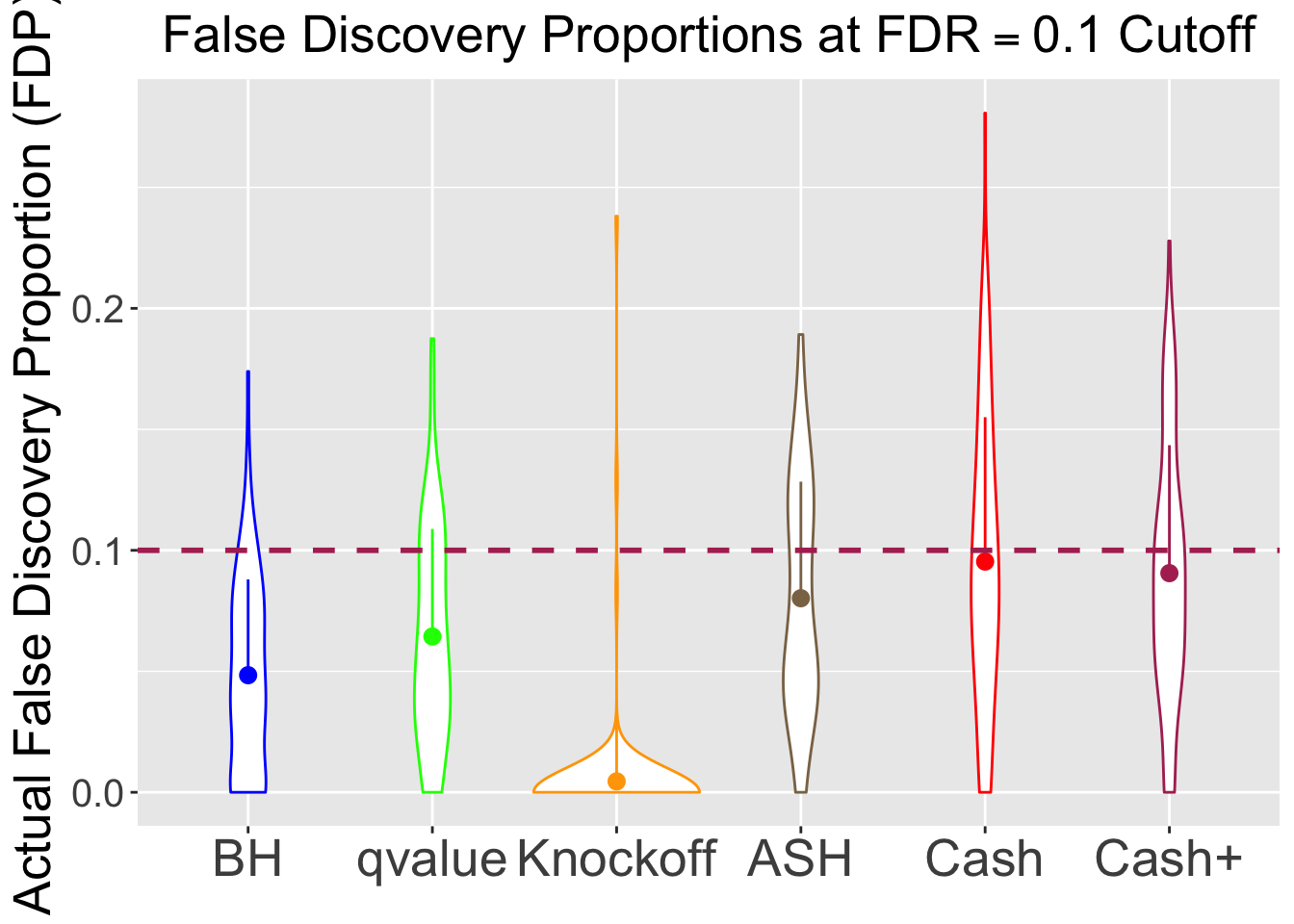
No id variables; using all as measure variables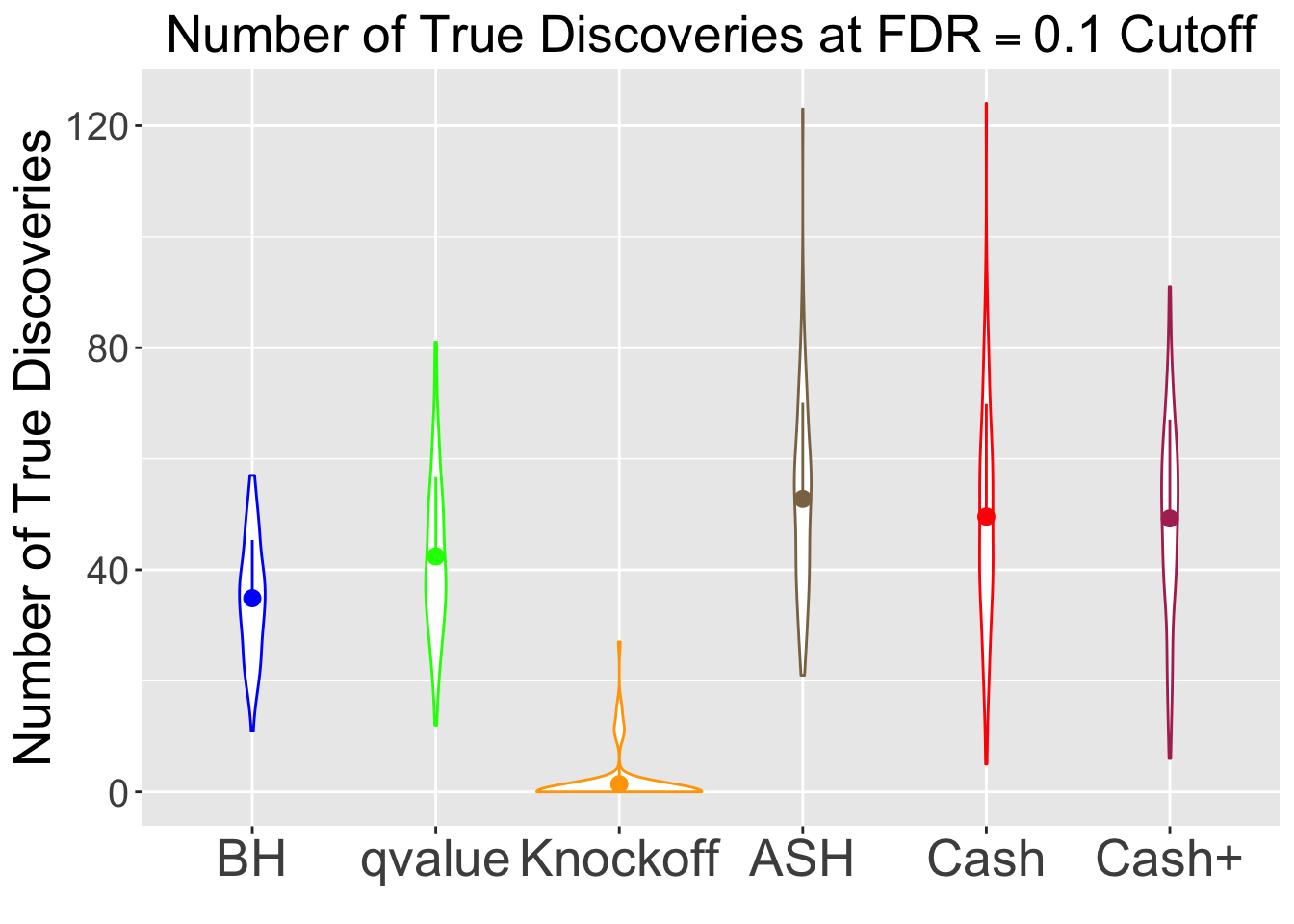
\(\eta = 0.9\), \(\sigma = 3\), \(\rho = 0.7\)
No id variables; using all as measure variables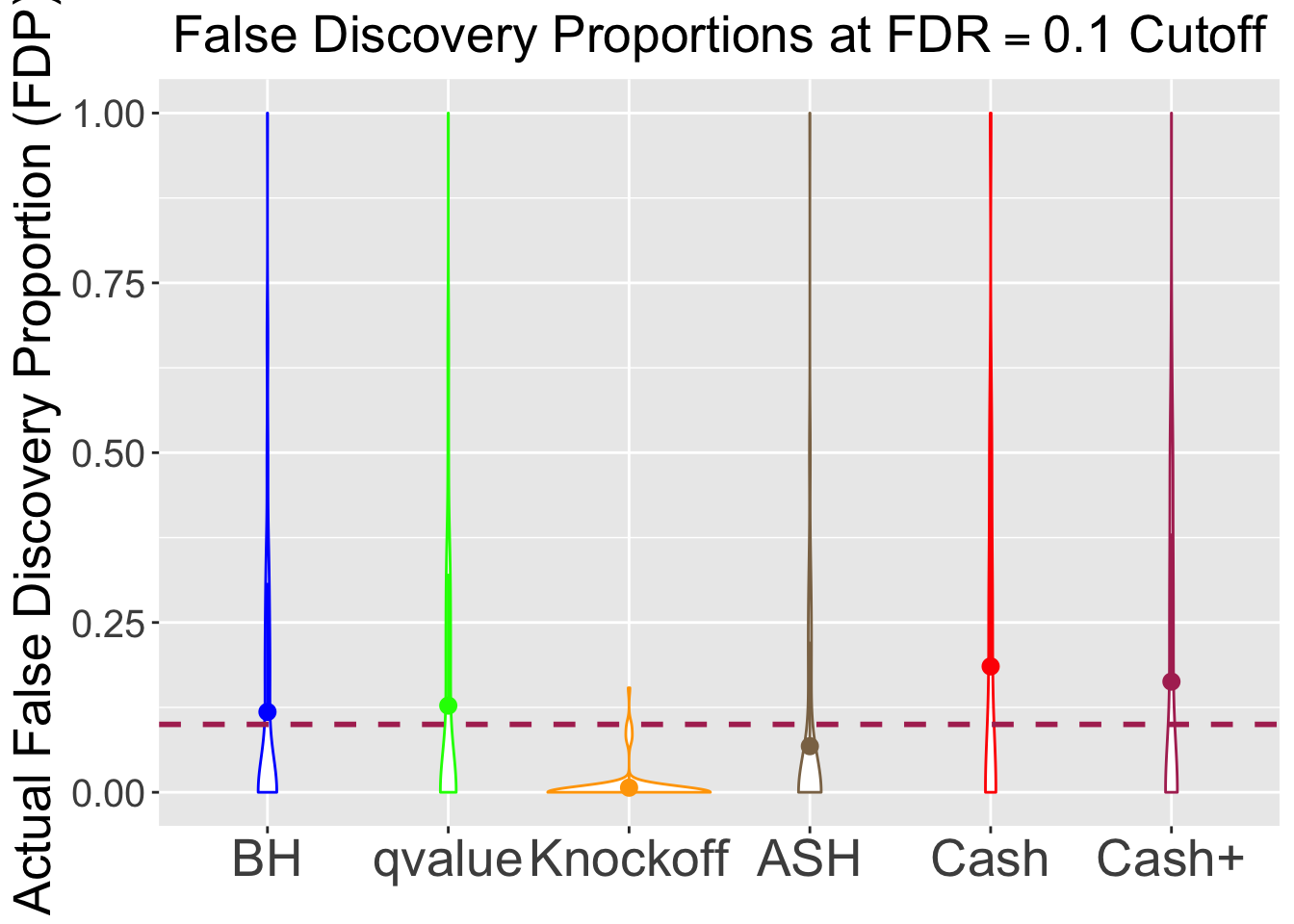
No id variables; using all as measure variables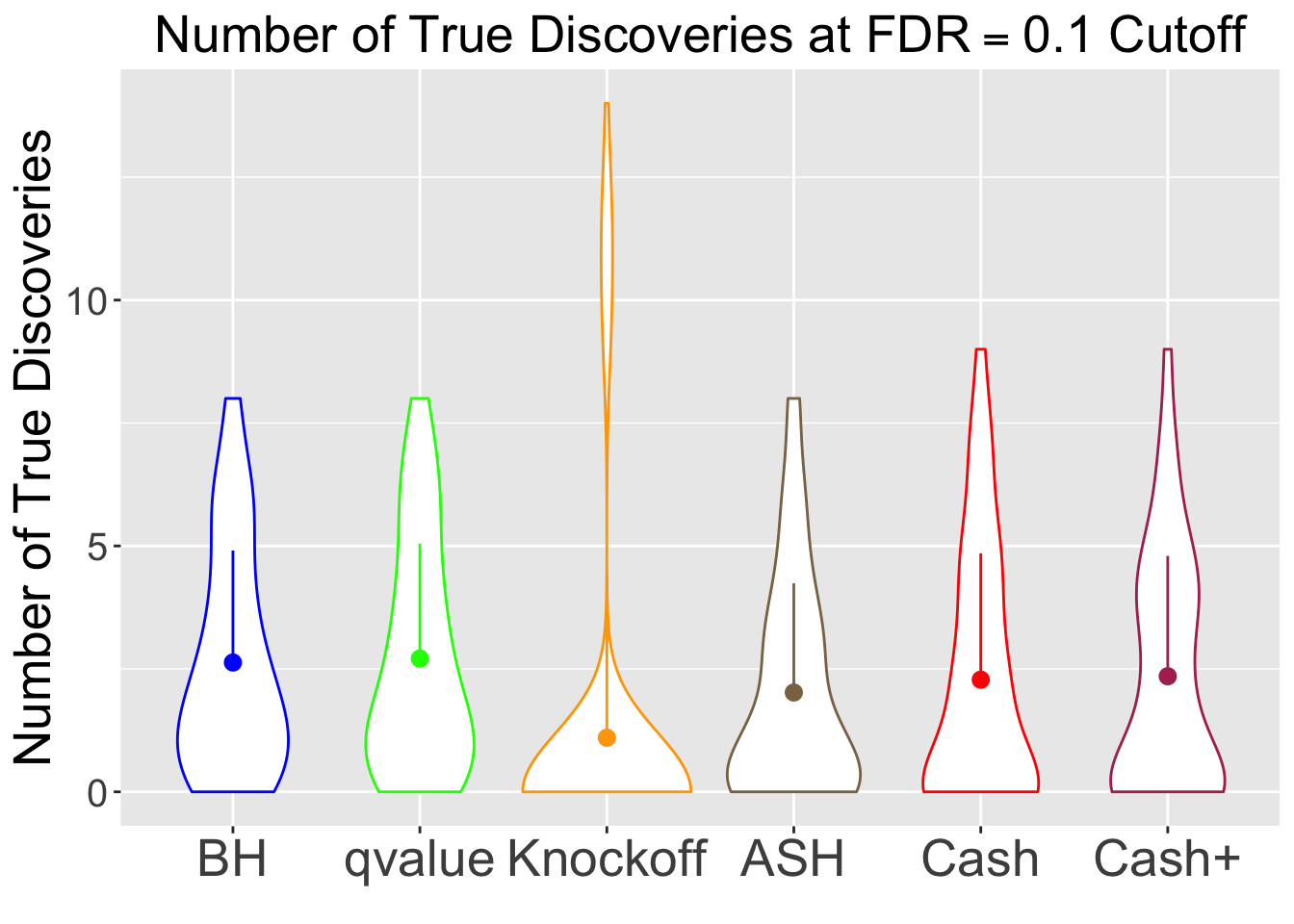
Session information
sessionInfo()R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.2
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] ggplot2_2.2.1 reshape2_1.4.3
loaded via a namespace (and not attached):
[1] Rcpp_0.12.14 knitr_1.18 magrittr_1.5 munsell_0.4.3
[5] colorspace_1.3-2 rlang_0.1.6 stringr_1.2.0 plyr_1.8.4
[9] tools_3.4.3 grid_3.4.3 gtable_0.2.0 git2r_0.21.0
[13] htmltools_0.3.6 yaml_2.1.16 lazyeval_0.2.1 rprojroot_1.3-2
[17] digest_0.6.14 tibble_1.4.1 evaluate_0.10.1 rmarkdown_1.8
[21] labeling_0.3 stringi_1.1.6 compiler_3.4.3 pillar_1.0.1
[25] scales_0.5.0 backports_1.1.2 This R Markdown site was created with workflowr