Factor Model for \(\hat\beta\) and Column Randomization for Knockoff
Lei Sun
2018-02-20
Last updated: 2018-04-05
Code version: 20ea328
Introduction
Knockoff has 3 steps.
Generate knockoff variables, which keep the same correlation structure as original variables but has no effect on the response.
Generate test statistics such that these statistics tend to be large positive number for non-null variables but iid positive or negative for null variables.
Find a cutoff threshold for those test statistics to control the estimated FDR under \(q\).
The default knockoff::knockoff.filter function uses SDP construction in step 1 and LASSO-related statistics in step 2. However, we’ve found that Knockoff coded in this way failed to control FDR in simulations when variables are generated such that \(\hat\beta\) has heavy average absolute pairwise correlation, which seems to contradict Theorem 2 in the Knockoff paper. Now we take a closer look to see what went wrong.
In step 1, we use two construction methods: equi and sdp. sdp is believed to be more powerful. In step 2, we use two statistics: marginal and lasso-related. lasso-related is believed to be more powerful.
n <- 3e3
p <- 1e3
k <- 50
d <- 7
q <- 0.1Fixed \(X\) Knockoffs: 1000 simulation trials
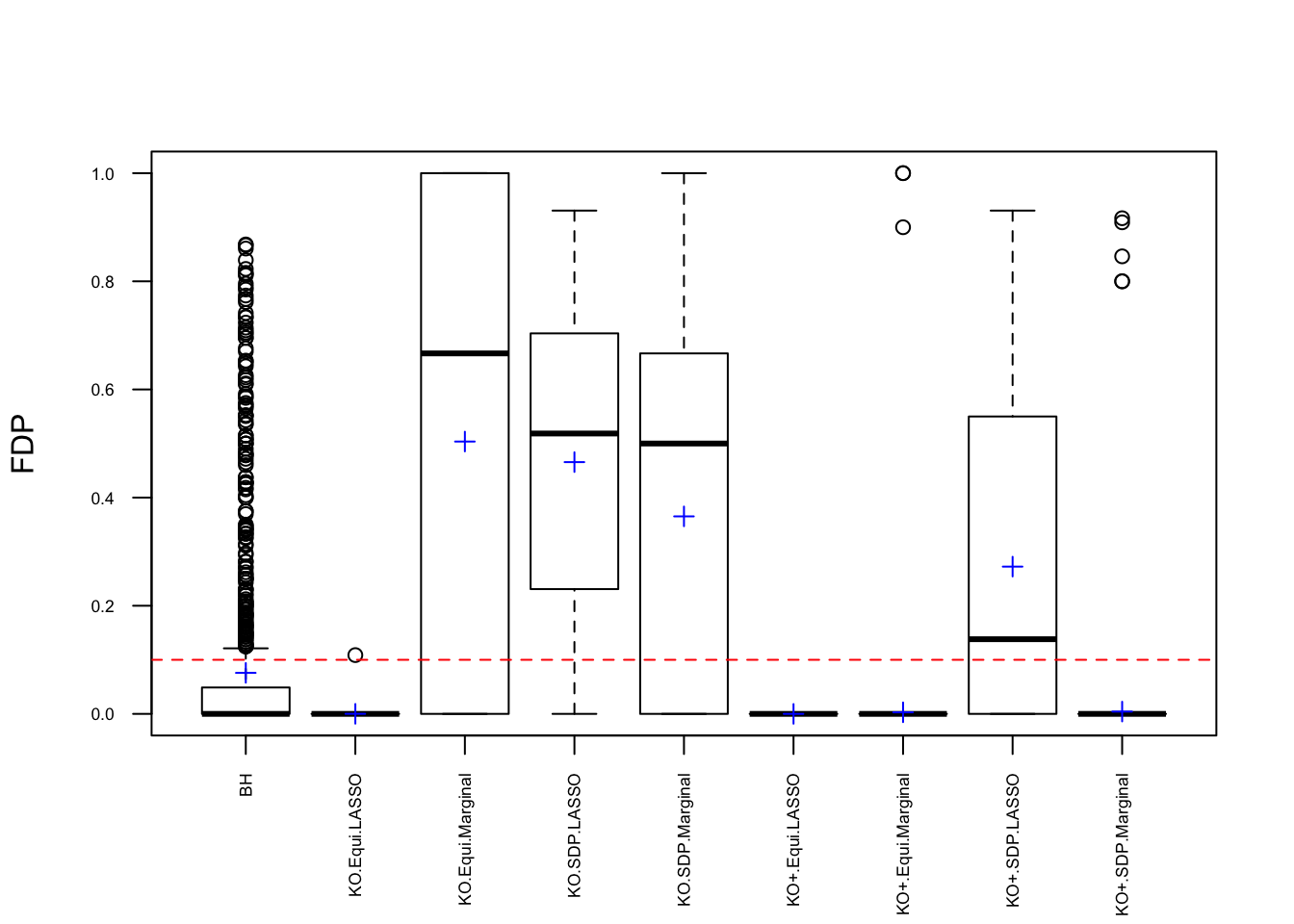

Model \(X\) Knockoffs: 1000 simulation trials
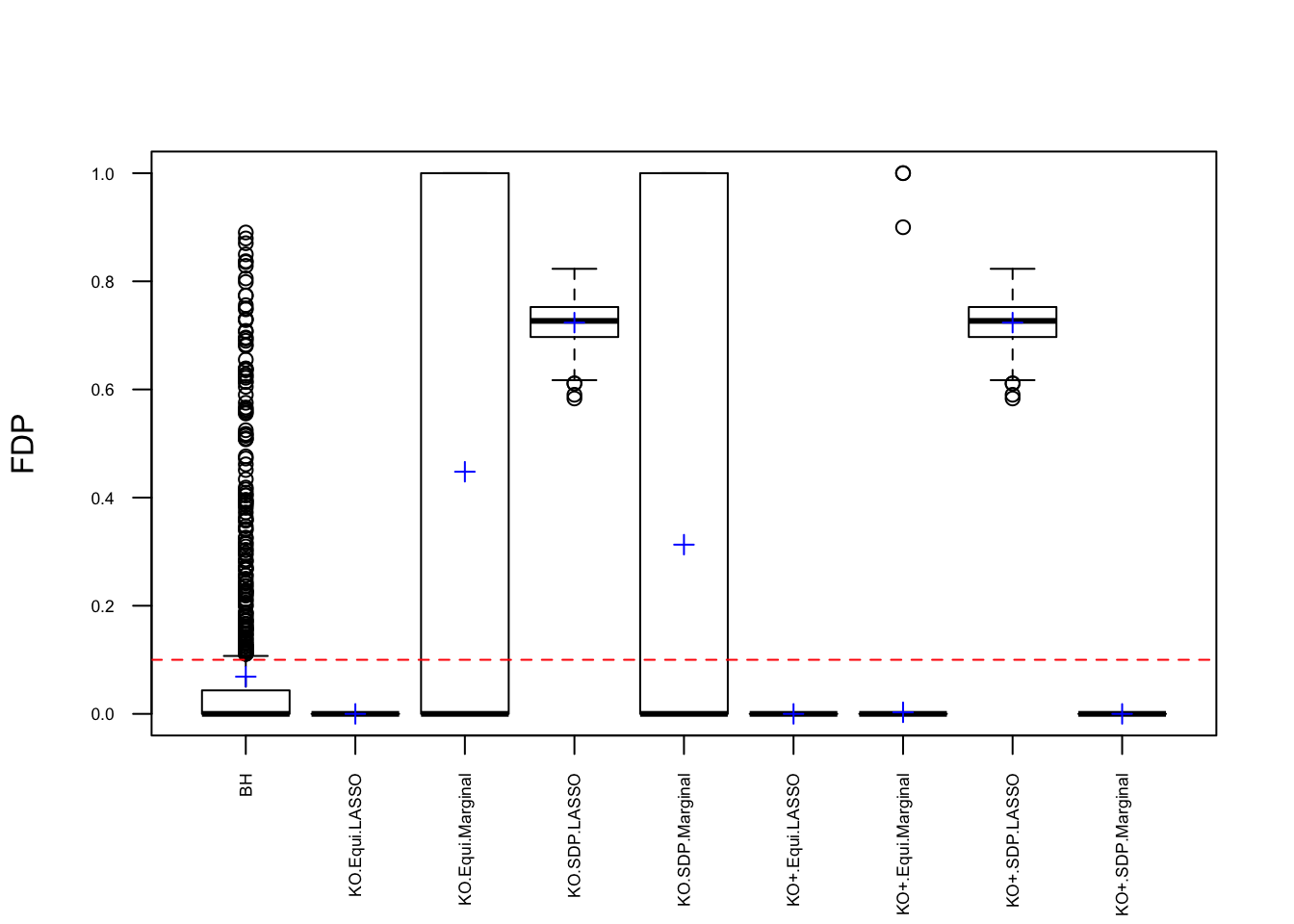
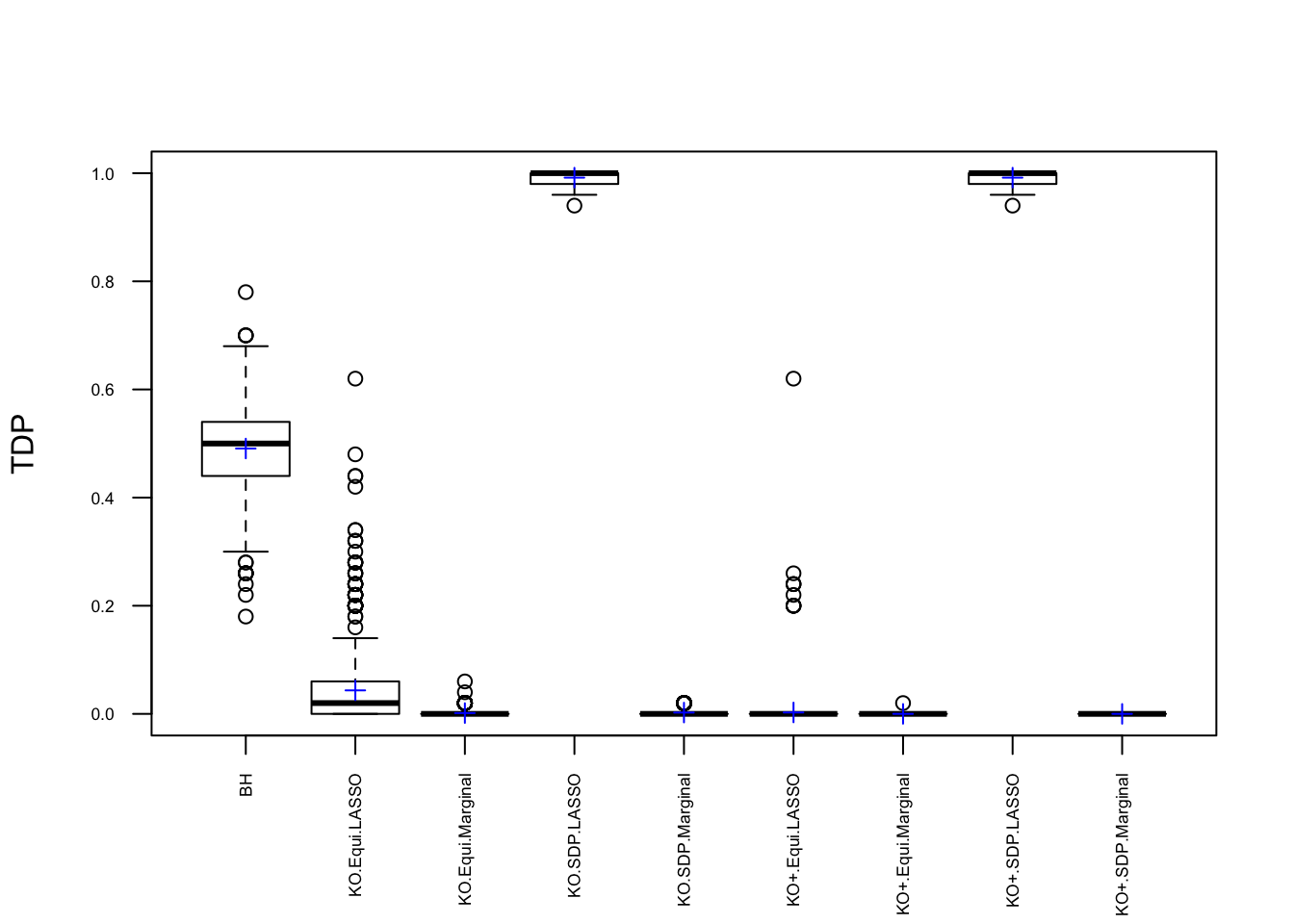
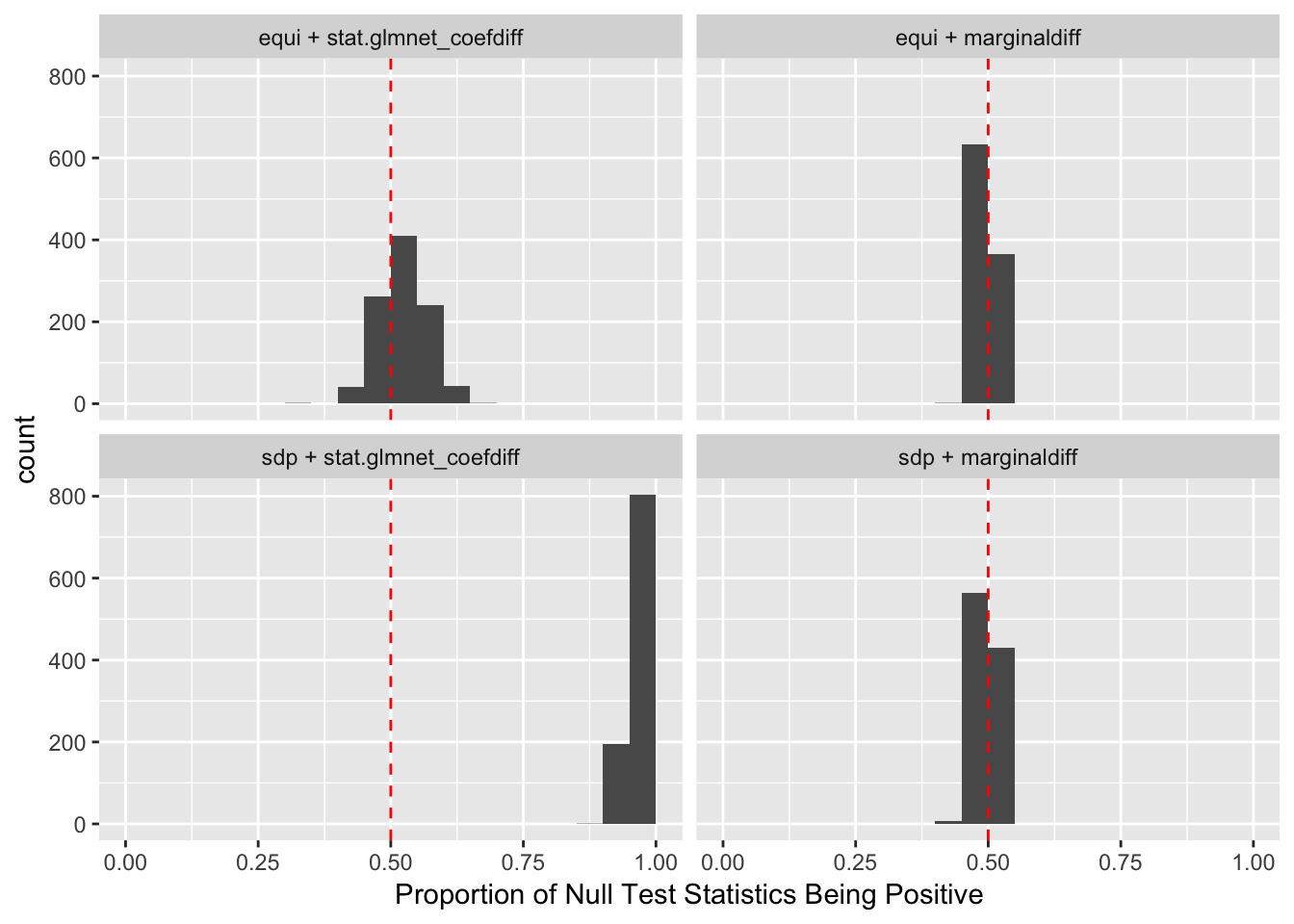
Observation
A set of well-bahaving Knockoff variables \(X^k\) should have the property that \[
\begin{array}{c}
cor(X^k_i, X^k_j) = cor(X_i, X_j)\\
cor(X_i, X^k_j) = cor(X_i, X_j)
\end{array}
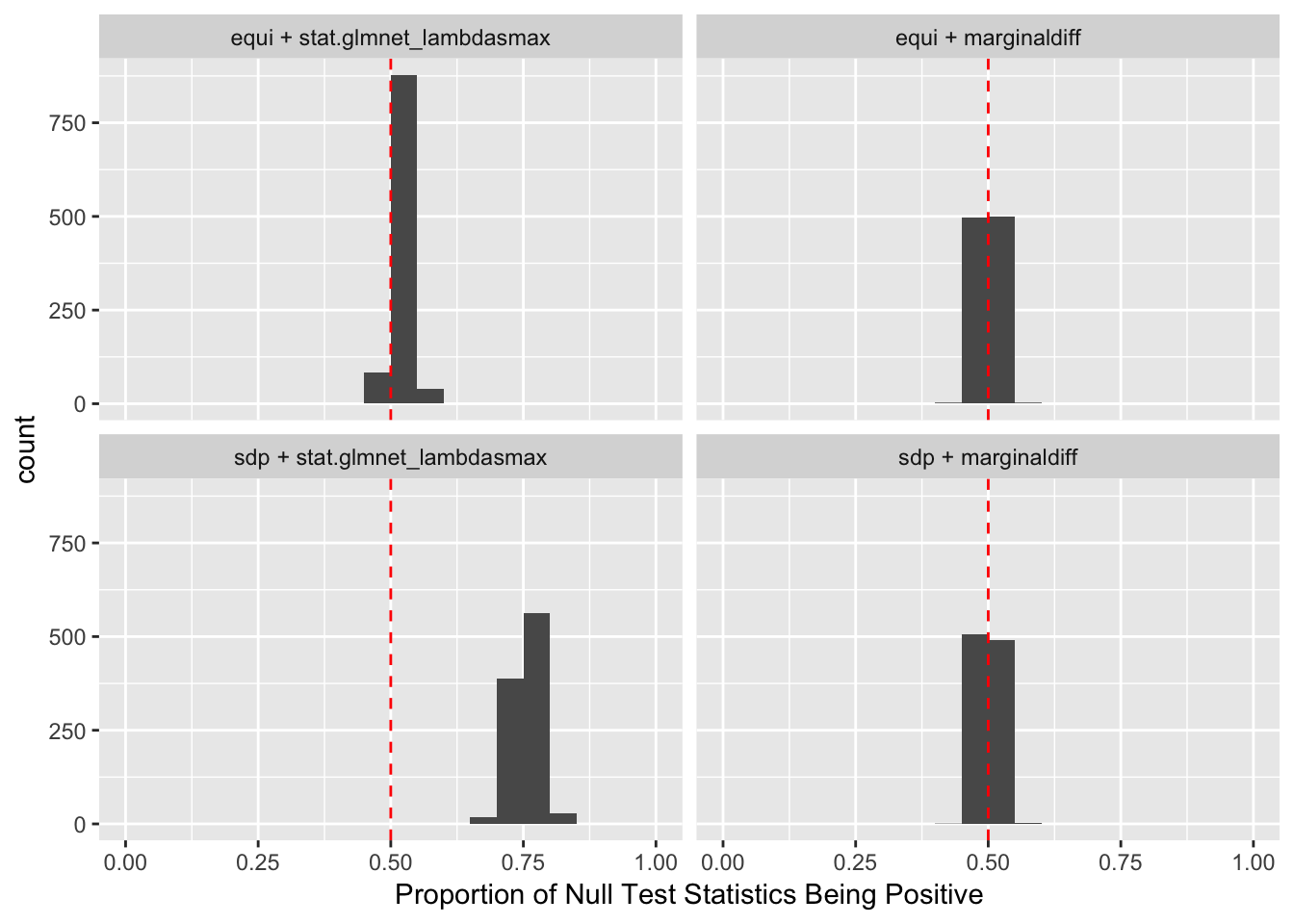
\] while \(cor(X_i, X^k_i)\) should be as small as possible. It turns out it’s just not that easy to generate these well-behaving Knockoff variables when columns in \(X\) are correlated in a certain way. Especially when using SDP optimization, it could generate a lot of knockoffs that are exactly the same as the originals.
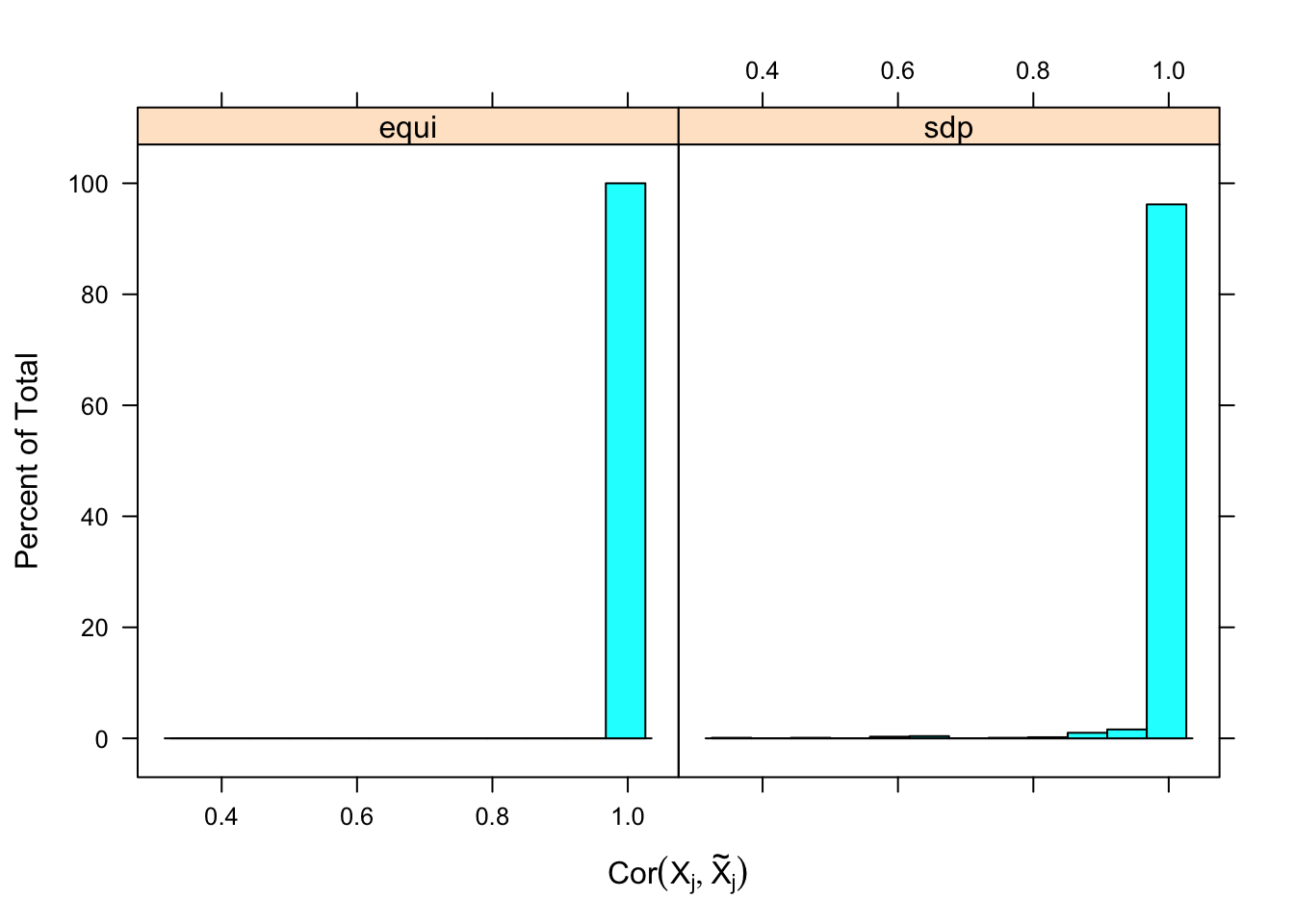
If an original variable and its knockoff are too similar, it essentially makes little difference which one is included in the model, from a goodness of fit point of view.
The problem becomes more severe when we fit models like LASSO using methods like coordinate descent. The result depends in large part on the sequence of variables getting into the model. So if we feed LASSO with cbind(X, Xk), for every iteration, it’s always X[j] being optimized before Xk[j]. That’s a major reason we see asymmetric test statistics as above, and why Knockoff loses FDR control in these circumstances.
One way to fix that is to randomize the order of variables in cbind(X, Xk) before feeding them to LASSO. The following is a simulation.
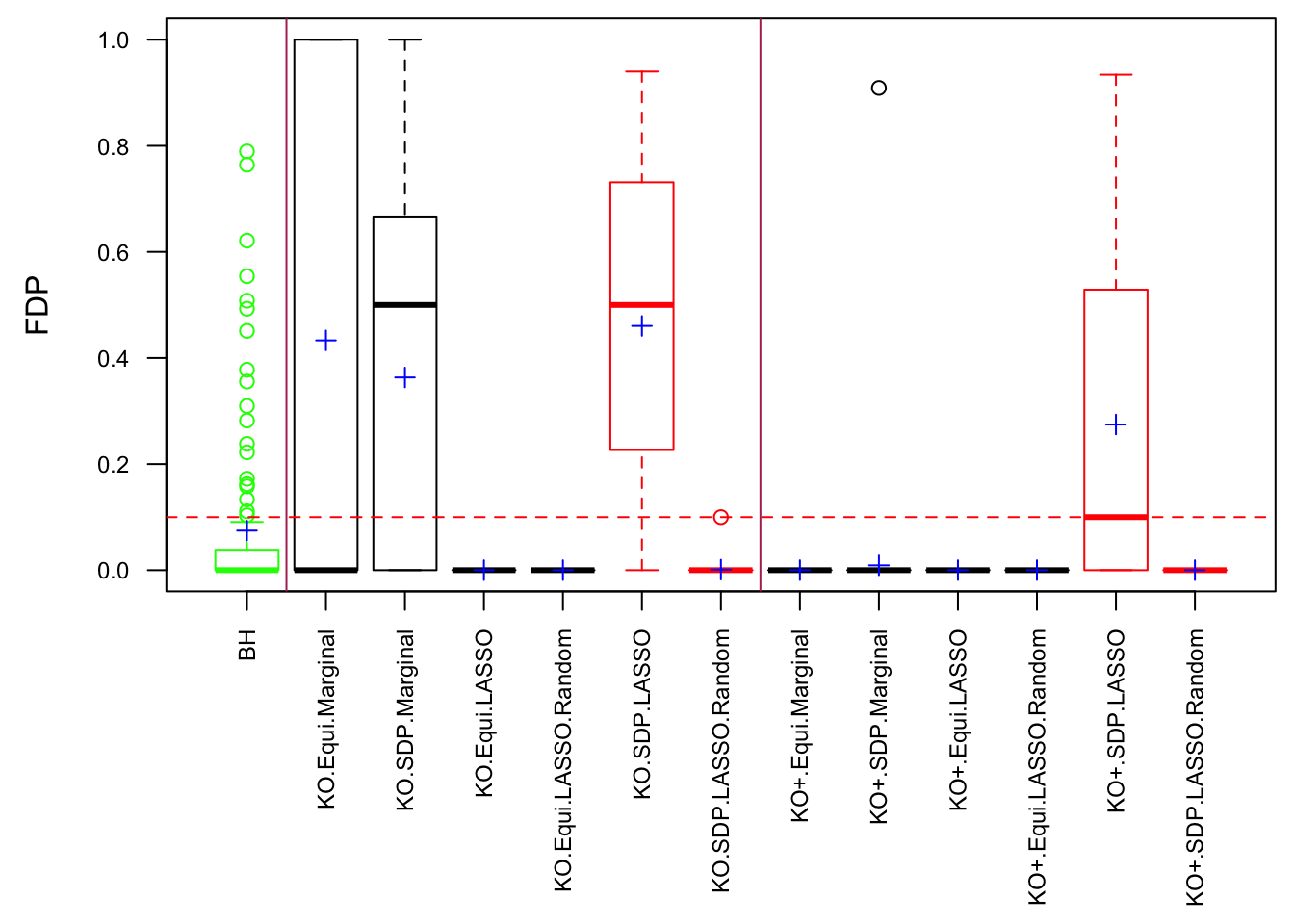
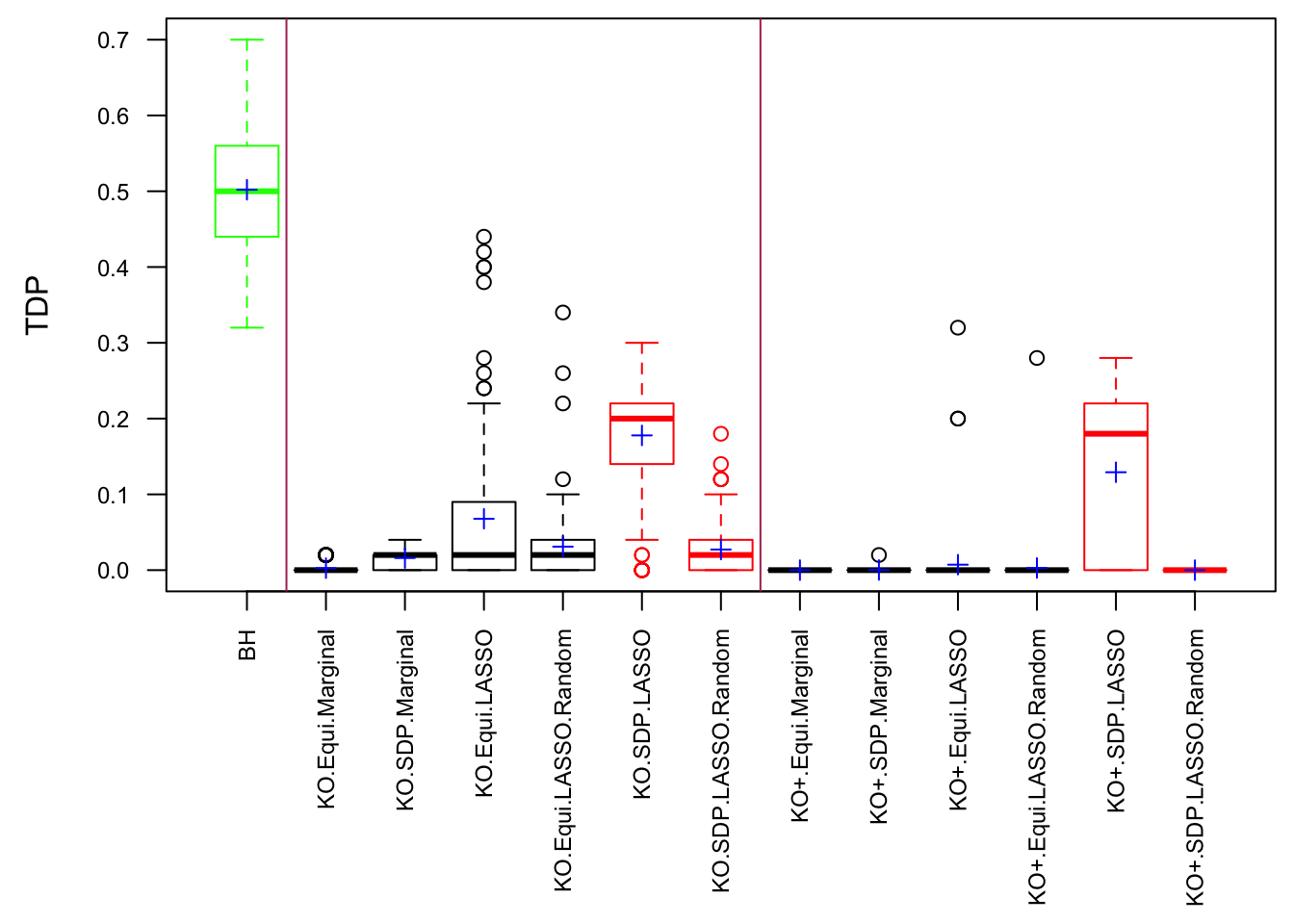
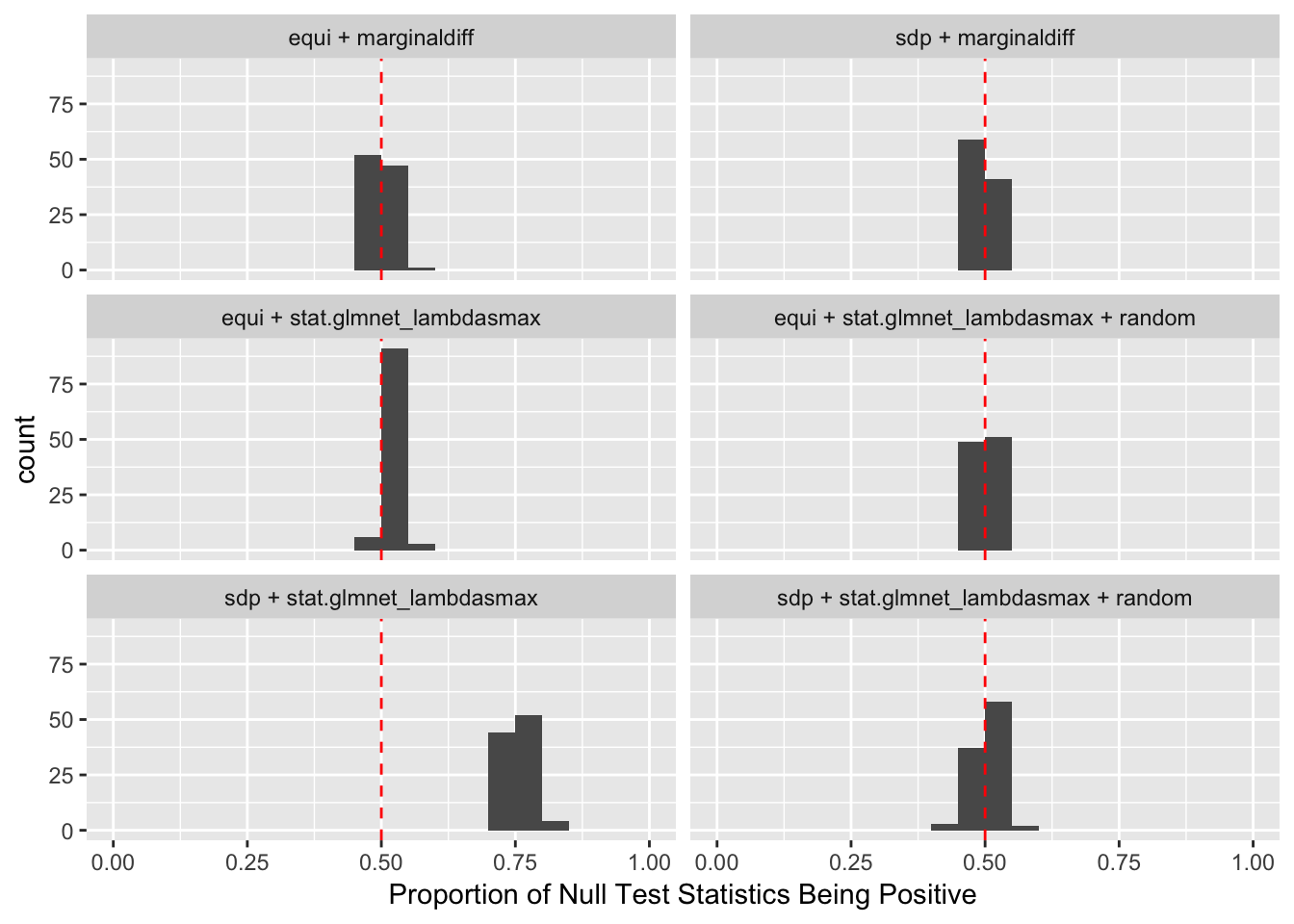
After column randomization, the test statistcs for null variables are back to normal and Knockoff controls FDR again. The low power is another issue.
Session information
sessionInfo()R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.4
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] parallel stats graphics grDevices utils datasets methods
[8] base
other attached packages:
[1] lattice_0.20-35 doMC_1.3.5 iterators_1.0.9 foreach_1.4.4
[5] ggplot2_2.2.1 reshape2_1.4.3 knockoff_0.3.0
loaded via a namespace (and not attached):
[1] Rcpp_0.12.14 knitr_1.20 magrittr_1.5 munsell_0.4.3
[5] colorspace_1.3-2 rlang_0.1.6 stringr_1.3.0 plyr_1.8.4
[9] tools_3.4.3 grid_3.4.3 gtable_0.2.0 RSpectra_0.12-0
[13] git2r_0.21.0 htmltools_0.3.6 yaml_2.1.18 lazyeval_0.2.1
[17] rprojroot_1.3-2 digest_0.6.15 tibble_1.4.1 Rdsdp_1.0.4-2
[21] Matrix_1.2-12 codetools_0.2-15 evaluate_0.10.1 rmarkdown_1.9
[25] labeling_0.3 stringi_1.1.6 pillar_1.0.1 compiler_3.4.3
[29] scales_0.5.0 backports_1.1.2 This R Markdown site was created with workflowr