<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<meta charset="utf-8" />
<meta http-equiv="Content-Type" content="text/html; charset=utf-8" />
<meta name="generator" content="pandoc" />
<meta name="author" content="Lei Sun" />
<meta name="date" content="2016-11-29" />
<title>FWER Procedures on Simulated Correlated Null</title>
<script src="site_libs/jquery-1.11.3/jquery.min.js"></script>
<meta name="viewport" content="width=device-width, initial-scale=1" />
<link href="site_libs/bootstrap-3.3.5/css/cosmo.min.css" rel="stylesheet" />
<script src="site_libs/bootstrap-3.3.5/js/bootstrap.min.js"></script>
<script src="site_libs/bootstrap-3.3.5/shim/html5shiv.min.js"></script>
<script src="site_libs/bootstrap-3.3.5/shim/respond.min.js"></script>
<script src="site_libs/jqueryui-1.11.4/jquery-ui.min.js"></script>
<link href="site_libs/tocify-1.9.1/jquery.tocify.css" rel="stylesheet" />
<script src="site_libs/tocify-1.9.1/jquery.tocify.js"></script>
<script src="site_libs/navigation-1.1/tabsets.js"></script>
<link href="site_libs/highlightjs-1.1/textmate.css" rel="stylesheet" />
<script src="site_libs/highlightjs-1.1/highlight.js"></script>
<link href="site_libs/font-awesome-4.5.0/css/font-awesome.min.css" rel="stylesheet" />
<style type="text/css">code{white-space: pre;}</style>
<style type="text/css">
pre:not([class]) {
background-color: white;
}
</style>
<script type="text/javascript">
if (window.hljs && document.readyState && document.readyState === "complete") {
window.setTimeout(function() {
hljs.initHighlighting();
}, 0);
}
</script>
<style type="text/css">
h1 {
font-size: 34px;
}
h1.title {
font-size: 38px;
}
h2 {
font-size: 30px;
}
h3 {
font-size: 24px;
}
h4 {
font-size: 18px;
}
h5 {
font-size: 16px;
}
h6 {
font-size: 12px;
}
.table th:not([align]) {
text-align: left;
}
</style>
</head>
<body>
<style type = "text/css">
.main-container {
max-width: 940px;
margin-left: auto;
margin-right: auto;
}
code {
color: inherit;
background-color: rgba(0, 0, 0, 0.04);
}
img {
max-width:100%;
height: auto;
}
.tabbed-pane {
padding-top: 12px;
}
button.code-folding-btn:focus {
outline: none;
}
</style>
<style type="text/css">
/* padding for bootstrap navbar */
body {
padding-top: 51px;
padding-bottom: 40px;
}
/* offset scroll position for anchor links (for fixed navbar) */
.section h1 {
padding-top: 56px;
margin-top: -56px;
}
.section h2 {
padding-top: 56px;
margin-top: -56px;
}
.section h3 {
padding-top: 56px;
margin-top: -56px;
}
.section h4 {
padding-top: 56px;
margin-top: -56px;
}
.section h5 {
padding-top: 56px;
margin-top: -56px;
}
.section h6 {
padding-top: 56px;
margin-top: -56px;
}
</style>
<script>
// manage active state of menu based on current page
$(document).ready(function () {
// active menu anchor
href = window.location.pathname
href = href.substr(href.lastIndexOf('/') + 1)
if (href === "")
href = "index.html";
var menuAnchor = $('a[href="' + href + '"]');
// mark it active
menuAnchor.parent().addClass('active');
// if it's got a parent navbar menu mark it active as well
menuAnchor.closest('li.dropdown').addClass('active');
});
</script>
<div class="container-fluid main-container">
<!-- tabsets -->
<script>
$(document).ready(function () {
window.buildTabsets("TOC");
});
</script>
<!-- code folding -->
<script>
$(document).ready(function () {
// move toc-ignore selectors from section div to header
$('div.section.toc-ignore')
.removeClass('toc-ignore')
.children('h1,h2,h3,h4,h5').addClass('toc-ignore');
// establish options
var options = {
selectors: "h1,h2,h3",
theme: "bootstrap3",
context: '.toc-content',
hashGenerator: function (text) {
return text.replace(/[.\\/?&!#<>]/g, '').replace(/\s/g, '_').toLowerCase();
},
ignoreSelector: ".toc-ignore",
scrollTo: 0
};
options.showAndHide = true;
options.smoothScroll = true;
// tocify
var toc = $("#TOC").tocify(options).data("toc-tocify");
});
</script>
<style type="text/css">
#TOC {
margin: 25px 0px 20px 0px;
}
@media (max-width: 768px) {
#TOC {
position: relative;
width: 100%;
}
}
.toc-content {
padding-left: 30px;
padding-right: 40px;
}
div.main-container {
max-width: 1200px;
}
div.tocify {
width: 20%;
max-width: 260px;
max-height: 85%;
}
@media (min-width: 768px) and (max-width: 991px) {
div.tocify {
width: 25%;
}
}
@media (max-width: 767px) {
div.tocify {
width: 100%;
max-width: none;
}
}
.tocify ul, .tocify li {
line-height: 20px;
}
.tocify-subheader .tocify-item {
font-size: 0.90em;
padding-left: 25px;
text-indent: 0;
}
.tocify .list-group-item {
border-radius: 0px;
}
</style>
<!-- setup 3col/9col grid for toc_float and main content -->
<div class="row-fluid">
<div class="col-xs-12 col-sm-4 col-md-3">
<div id="TOC" class="tocify">
</div>
</div>
<div class="toc-content col-xs-12 col-sm-8 col-md-9">
<div class="navbar navbar-default navbar-fixed-top" role="navigation">
<div class="container">
<div class="navbar-header">
<button type="button" class="navbar-toggle collapsed" data-toggle="collapse" data-target="#navbar">
<span class="icon-bar"></span>
<span class="icon-bar"></span>
<span class="icon-bar"></span>
</button>
<a class="navbar-brand" href="index.html">truncash</a>
</div>
<div id="navbar" class="navbar-collapse collapse">
<ul class="nav navbar-nav">
<li>
<a href="index.html">Home</a>
</li>
<li>
<a href="about.html">About</a>
</li>
<li>
<a href="license.html">License</a>
</li>
</ul>
<ul class="nav navbar-nav navbar-right">
<li>
<a href="https://github.com/LSun/truncash">
<span class="fa fa-github"></span>
</a>
</li>
</ul>
</div><!--/.nav-collapse -->
</div><!--/.container -->
</div><!--/.navbar -->
<div class="fluid-row" id="header">
<h1 class="title toc-ignore">FWER Procedures on Simulated Correlated Null</h1>
<h4 class="author"><em>Lei Sun</em></h4>
<h4 class="date"><em>2016-11-29</em></h4>
</div>
<p><strong>Last updated:</strong> 2017-11-07</p>
<p><strong>Code version:</strong> 2c05d59</p>
<div id="introduction" class="section level2">
<h2>Introduction</h2>
<p>In order to understand the behavior of <span class="math inline">\(p\)</span>-values of top expressed, correlated genes under the global null, simulated from GTEx data, we apply two FWER-controlling multiple comparison procedures, Holm’s “step-down” (<a href="http://www.jstor.org/stable/4615733?seq=1#page_scan_tab_contents">Holm 1979</a>) and Hochberg’s “step-up.” (<a href="https://academic.oup.com/biomet/article-abstract/75/4/800/423177/A-sharper-Bonferroni-procedure-for-multiple-tests">Hochberg 1988</a>)</p>
</div>
<div id="holms-step-down-procedure-start-from-the-smallest-p-value" class="section level2">
<h2>Holm’s step-down procedure: start from the smallest <span class="math inline">\(p\)</span>-value</h2>
<p><em>It can be shown that Holm’s procedure conservatively controls the FWER in the strong sense, under arbitrary correlation among <span class="math inline">\(p\)</span>-values.</em></p>
<p>First, order the <span class="math inline">\(p\)</span>-values</p>
<p><span class="math display">\[
p_{(1)} \leq p_{(2)} \leq \cdots \leq p_{(n)}
\]</span></p>
<p>and let <span class="math inline">\(H_{(1)}, H_{(2)}, \ldots, H_{(n)}\)</span> be the corresponding hypotheses. Then examine the <span class="math inline">\(p\)</span>-values in order.</p>
<p>Step 1: If <span class="math inline">\(p_{(1)} \leq \alpha/n\)</span> reject <span class="math inline">\(H_{(1)}\)</span> and go to Step 2. Otherwise, accept <span class="math inline">\(H_{(1)}, H_{(2)}, \ldots, H_{(n)}\)</span> and stop.</p>
<p>……</p>
<p>Step <span class="math inline">\(i\)</span>: If <span class="math inline">\(p_{(i)} \leq \alpha / (n − i + 1)\)</span> reject <span class="math inline">\(H_{(i)}\)</span> and go to step <span class="math inline">\(i + 1\)</span>. Otherwise, accept <span class="math inline">\(H_{(i)}, H_{(i + 1)}, \ldots, H_{(n)}\)</span> and stop.</p>
<p>……</p>
<p>Step <span class="math inline">\(n\)</span>: If <span class="math inline">\(p_{(n)} \leq \alpha\)</span>, reject <span class="math inline">\(H_{(n)}\)</span>. Otherwise, accept <span class="math inline">\(H_{(n)}\)</span>.</p>
<p>Hence the procedure starts with the most extreme (smallest) <span class="math inline">\(p\)</span>-value and stops the first time <span class="math inline">\(p_{(i)}\)</span> exceeds the critical value <span class="math inline">\(\alpha_i = \alpha/(n − i + 1)\)</span>.</p>
<p><strong>It can be shown that Holm’s procedure conservatively controls the FWER in the strong sense, under arbitrary correlation among <span class="math inline">\(p\)</span>-values.</strong></p>
</div>
<div id="hochbergs-step-up-procedure-start-from-the-largest-p-value" class="section level2">
<h2>Hochberg’s step-up procedure: start from the largest <span class="math inline">\(p\)</span>-value</h2>
<p><em>It can be shown that Hochberg’s procedure conservatively controls the FWER in the strong sense, when <span class="math inline">\(p\)</span>-values are independent.</em></p>
<p>First, order the <span class="math inline">\(p\)</span>-values</p>
<p><span class="math display">\[
p_{(1)} \leq p_{(2)} \leq \cdots \leq p_{(n)}
\]</span></p>
<p>and let <span class="math inline">\(H_{(1)}, H_{(2)}, \ldots, H_{(n)}\)</span> be the corresponding hypotheses. Then examine the <span class="math inline">\(p\)</span>-values in order.</p>
<p>Step 1: If <span class="math inline">\(p_{(n)} \leq \alpha\)</span> reject <span class="math inline">\(H_{(1)}, \ldots, H_{(n)}\)</span> and stop. Otherwise, accept <span class="math inline">\(H_{(n)}\)</span> and go to step 2.</p>
<p>……</p>
<p>Step <span class="math inline">\(i\)</span>: If <span class="math inline">\(p_{(n - i + 1)} \leq \alpha / i\)</span> reject <span class="math inline">\(H_{(1)}, \ldots, H_{(n - i + 1)}\)</span> and stop. Otherwise, accept <span class="math inline">\(H_{(n - i + 1)}\)</span> and go to step <span class="math inline">\(i + 1\)</span>.</p>
<p>……</p>
<p>Step <span class="math inline">\(n\)</span>: If <span class="math inline">\(p_{(1)} \leq \alpha / n\)</span>, reject <span class="math inline">\(H_{(1)}\)</span>. Otherwise, accept <span class="math inline">\(H_{(1)}\)</span>.</p>
<p>Hence the procedure starts with the least extreme (largest) <span class="math inline">\(p\)</span>-value and stops the first time <span class="math inline">\(p_{(i)}\)</span> falls below the critical value <span class="math inline">\(\alpha_i = \alpha/(n − i + 1)\)</span>.</p>
<p><strong>It can be shown that Hochberg’s procedure conservatively controls the FWER in the strong sense, when <span class="math inline">\(p\)</span>-values are independent.</strong></p>
<p><strong><a href="https://projecteuclid.org/euclid.aos/1028144846">Sarkar 1998</a> also pointed out that Hochberg’s procedure can control the FWER strongly under certain dependency among the test statistics, such as a multivariate normal with a common marginal distribution and positive correlations.</strong></p>
<p><strong>Holm’s procedure is based on Bonferroni correction, whereas Hochberg’s on Sime’s inequality. Both use exactly the same thresholds, comparing <span class="math inline">\(p_{(i)}\)</span> with <span class="math inline">\(\alpha/(n − i + 1)\)</span>, yet Holm’s starts from the smallest <span class="math inline">\(p\)</span>-value, and Hochberg’s from the largest. Hochberg’s is thus strictly more powerful than Holm’s.</strong></p>
</div>
<div id="result" class="section level2">
<h2>Result</h2>
<p>Now we apply the two procedures to the simulated, correlated null data.</p>
<pre class="r"><code>p1 = read.table("../output/p_null_liver.txt")
p2 = read.table("../output/p_null_liver_777.txt")
p = rbind(p1, p2)
m = nrow(p)
holm = hochberg = matrix(nrow = m, ncol = ncol(p))
for(i in 1:m){
holm[i, ] = p.adjust(p[i, ], method = "holm") # p-values adjusted by Holm (1979)
hochberg[i, ] = p.adjust(p[i, ], method = "hochberg") # p_values adjusted by Hochberg (1988)
}</code></pre>
<pre class="r"><code>## calculate empirical FWER at 100 nominal FWER's
alpha = seq(0, 0.15, length = 100)
fwer_holm = fwer_hochberg = c()
for (i in 1:length(alpha)) {
fwer_holm[i] = mean(apply(holm, 1, function(x) {min(x) <= alpha[i]}))
fwer_hochberg[i] = mean(apply(hochberg, 1, function(x) {min(x) <= alpha[i]}))
}
fwer_holm_se = sqrt(fwer_holm * (1 - fwer_holm) / m)
fwer_hochberg_se = sqrt(fwer_hochberg * (1 - fwer_hochberg) / m)</code></pre>
<p>Here at each nominal FWER from <span class="math inline">\(0\)</span> to <span class="math inline">\(0.15\)</span>, we plot the empirical FWER, calculated from <span class="math inline">\(m = 2000\)</span> independent simulation trials. Dotted lines indicate one standard error computed from binomial model <span class="math inline">\(= \sqrt{\hat{\text{FWER}}(1 - \hat{\text{FWER}}) / m}\)</span>.</p>
<pre class="r"><code>plot(alpha, fwer_holm, pch = 1, xlab = "nominal FWER", ylab = "empirical FWER", xlim = c(0, max(alpha)), ylim = c(0, max(alpha)), cex = 0.75)
points(alpha, fwer_hochberg, col = "blue", pch = 19, cex = 0.25)
lines(alpha, fwer_holm - fwer_holm_se, lty = 3)
lines(alpha, fwer_holm + fwer_holm_se, lty = 3)
lines(alpha, fwer_hochberg + fwer_hochberg_se, lty = 3, col = "blue")
lines(alpha, fwer_hochberg - fwer_hochberg_se, lty = 3, col = "blue")
abline(0, 1, lty = 3, col = "red")
legend("topleft", c("Holm", "Hochberg"), col = c(1, "blue"), pch = c(1, 19))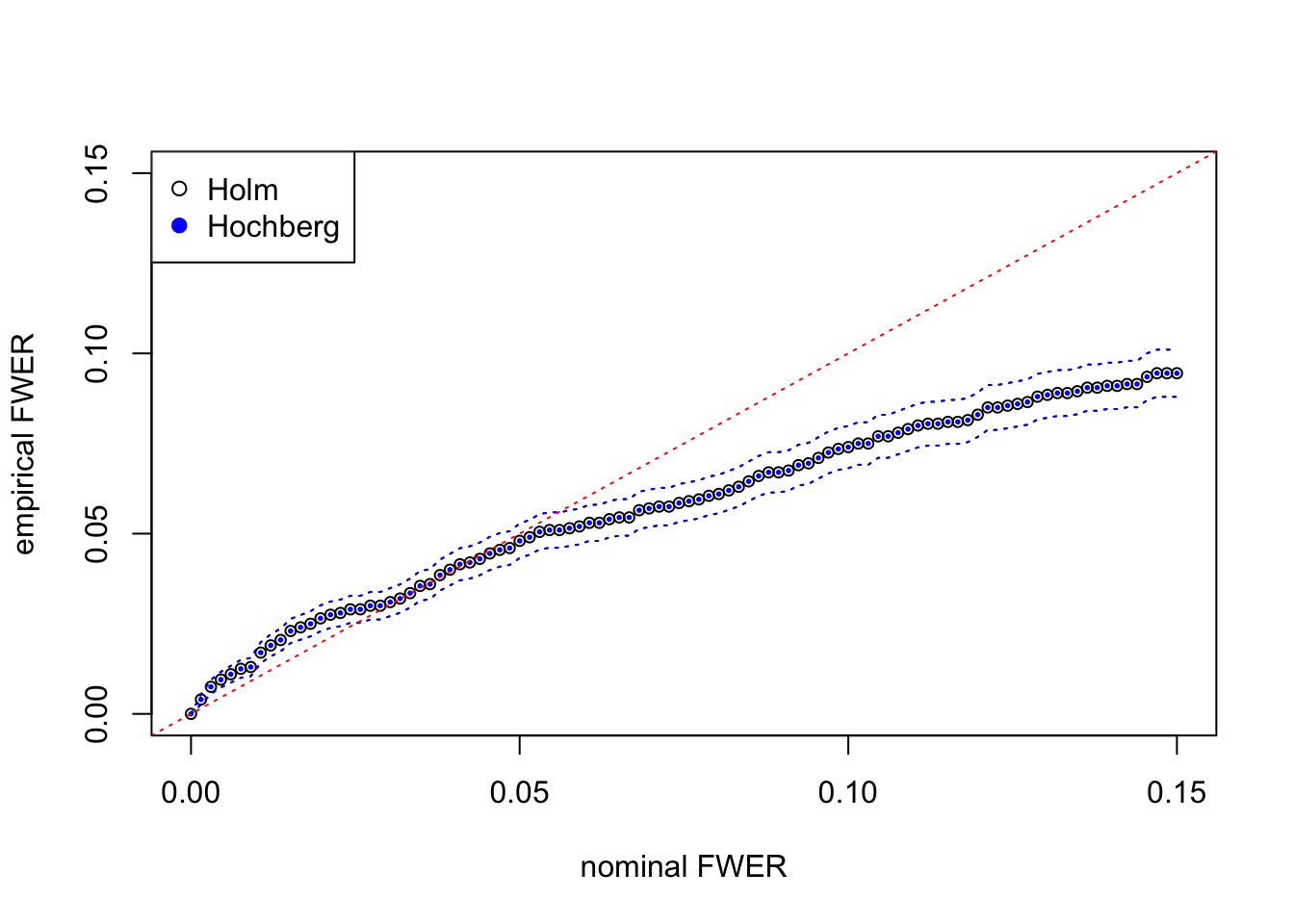</code></pre>
<p><img src="figure/StepDown.Rmd/unnamed-chunk-3-1.png" width="672" style="display: block; margin: auto;" /></p>
<p>The results from Holm’s step-down and Hochberg’s step-up are almost the same for this simulated data set. They both give almost the same discoveries, although in theory Hochberg’s should be strictly more powerful than Holm’s. <em>The agreement of both procedures may indicate that test statistics are indeed inflated for moderate observations but not extreme observations.</em></p>
</div>
<div id="session-information" class="section level2">
<h2>Session Information</h2>
<pre class="r"><code>sessionInfo()</code></pre>
<pre><code>R version 3.4.2 (2017-09-28)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS Sierra 10.12.6
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
loaded via a namespace (and not attached):
[1] compiler_3.4.2 backports_1.1.1 magrittr_1.5 rprojroot_1.2
[5] tools_3.4.2 htmltools_0.3.6 yaml_2.1.14 Rcpp_0.12.13
[9] stringi_1.1.5 rmarkdown_1.6 knitr_1.17 git2r_0.19.0
[13] stringr_1.2.0 digest_0.6.12 workflowr_0.7.0 evaluate_0.10.1</code></pre>
</div>
<hr>
<p>
This <a href="http://rmarkdown.rstudio.com">R Markdown</a> site was created with <a href="https://github.com/jdblischak/workflowr">workflowr</a>
</p>
<hr>
<!-- To enable disqus, uncomment the section below and provide your disqus_shortname -->
<!-- disqus
<div id="disqus_thread"></div>
<script type="text/javascript">
/* * * CONFIGURATION VARIABLES: EDIT BEFORE PASTING INTO YOUR WEBPAGE * * */
var disqus_shortname = 'rmarkdown'; // required: replace example with your forum shortname
/* * * DON'T EDIT BELOW THIS LINE * * */
(function() {
var dsq = document.createElement('script'); dsq.type = 'text/javascript'; dsq.async = true;
dsq.src = '//' + disqus_shortname + '.disqus.com/embed.js';
(document.getElementsByTagName('head')[0] || document.getElementsByTagName('body')[0]).appendChild(dsq);
})();
</script>
<noscript>Please enable JavaScript to view the <a href="http://disqus.com/?ref_noscript">comments powered by Disqus.</a></noscript>
<a href="http://disqus.com" class="dsq-brlink">comments powered by <span class="logo-disqus">Disqus</span></a>
-->
</div>
</div>
</div>
<script>
// add bootstrap table styles to pandoc tables
function bootstrapStylePandocTables() {
$('tr.header').parent('thead').parent('table').addClass('table table-condensed');
}
$(document).ready(function () {
bootstrapStylePandocTables();
});
</script>
<!-- dynamically load mathjax for compatibility with self-contained -->
<script>
(function () {
var script = document.createElement("script");
script.type = "text/javascript";
script.src = "https://mathjax.rstudio.com/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML";
document.getElementsByTagName("head")[0].appendChild(script);
})();
</script>
</body>
</html>