<!DOCTYPE html>
<html>
<head>
<title>Logistic Regression With Regularization</title>
<meta charset="utf-8">
<meta name="description" content="Logistic Regression With Regularization">
<meta name="author" content="Devin Riley">
<meta name="generator" content="slidify" />
<meta name="apple-mobile-web-app-capable" content="yes">
<meta http-equiv="X-UA-Compatible" content="chrome=1">
<link rel="stylesheet" href="libraries/frameworks/io2012/css/default.css" media="all" >
<link rel="stylesheet" href="libraries/frameworks/io2012/css/phone.css"
media="only screen and (max-device-width: 480px)" >
<link rel="stylesheet" href="libraries/frameworks/io2012/css/slidify.css" >
<link rel="stylesheet" href="libraries/highlighters/highlight.js/css/tomorrow.css" />
<base target="_blank"> <!-- This amazingness opens all links in a new tab. --> <link rel=stylesheet href="libraries/widgets/bootstrap/css/bootstrap.css"></link>
<link rel=stylesheet href="./assets/css/ribbons.css"></link>
<!-- Grab CDN jQuery, fall back to local if offline -->
<script src="http://ajax.aspnetcdn.com/ajax/jQuery/jquery-1.7.min.js"></script>
<script>window.jQuery || document.write('<script src="libraries/widgets/quiz/js/jquery.js"><\/script>')</script>
<script data-main="libraries/frameworks/io2012/js/slides"
src="libraries/frameworks/io2012/js/require-1.0.8.min.js">
</script>
</head>
<body style="opacity: 0">
<slides class="layout-widescreen">
<!-- LOGO SLIDE -->
<slide class="title-slide segue nobackground">
<hgroup class="auto-fadein">
<h1>Logistic Regression With Regularization</h1>
<h2>Ann Arbor R User Group, April 2015</h2>
<p>Devin Riley<br/></p>
</hgroup>
<article></article>
</slide>
<!-- SLIDES -->
<slide class="" id="slide-1" style="background:;">
<hgroup>
<h2>Overview</h2>
</hgroup>
<article data-timings="">
<ul>
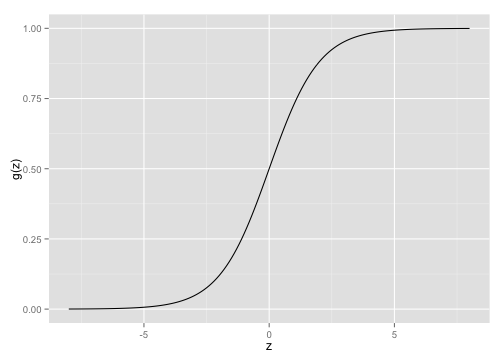
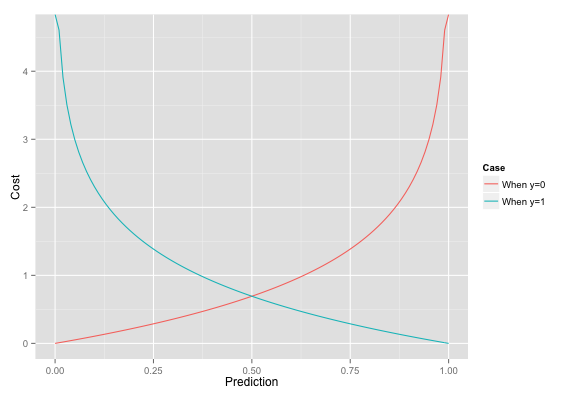
<li>Brief intro to logistic regression</li>
<li>Motivation for regularization techniques</li>
<li>Explanation of the most common regularization techniques:<br>
<ul>
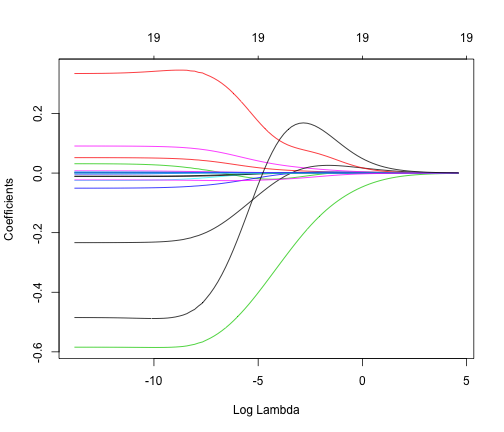
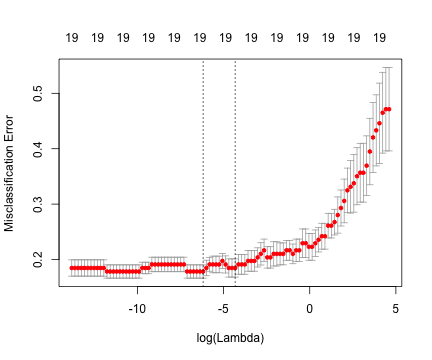
<li>Ridge regression</li>
<li>Lasso regression</li>
</ul></li>
<li>An example of each on a sample dataset</li>
</ul>
<p><br/>
<br/>
R packages to install if you want to follow along:</p>
<pre><code class="r">pkgs <- c('glmnet', 'ISLR')
install.packages(pkgs)
</code></pre>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-2" style="background:;">
<hgroup>
<h2>Logistic Regression</h2>
</hgroup>
<article data-timings="">
<p>Widely utilized <em>classification</em> technique.<br>
Regression for when the response variable is qualitative.<br>
Special case of the general linear model.<br>
For a response \(y\), model the probability that \(y\) belongs to a particular class or category. </p>
<p>\[y \in \{0, 1\}\]</p>
<p>With respect to a simple linear regression, we can think of it as:
\[p^'_\beta(x) = \beta^T x = \beta_0 + \beta_1 x_1 + ... + \beta_p x_p\]</p>
<p>Where we would <em>like</em> \(p^'_\beta(x)\) to represent the probability that x belongs to a particular class<br>
But, this formulation does not fit the definition of probability (i.e. on [0,1]), so need model representation, \(p_\beta(x)\) s.t.: </p>
<p>\[ 0 \le p_\beta \le 1\]</p>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-3" style="background:;">
<hgroup>
<h2>The logistic function</h2>
</hgroup>
<article data-timings="">
<p>AKA Sigmoid function:<br>
\[g(z) = \dfrac{1}{1 + e^{-z}}\]</p>
<p><img src="assets/fig/unnamed-chunk-2.png" title="plot of chunk unnamed-chunk-2" alt="plot of chunk unnamed-chunk-2" style="display: block; margin: auto;" /></p>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-4" style="background:;">
<hgroup>
<h2>Logistic Regression</h2>
</hgroup>
<article data-timings="">
<p>So if our original representation was<br>
\[p^'_\beta(x) = \beta^T x\]
then our representation becomes<br>
\[p_\beta(x) = g(p^'_\beta(x)) = g(\beta^T x)\] </p>
<p>where g(z), again, is
\[g(z) = \dfrac{1}{1 + e^{-z}}\]</p>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-5" style="background:;">
<hgroup>
<h2>Logistic Regression</h2>
</hgroup>
<article data-timings="">
<p>So,
\[p_\beta(x) = \dfrac{1}{1 + e^{-\beta^T x}}\]</p>
<p>After a bit of manipulation, we have<br>
\[ \dfrac{p_\beta(x)}{1-p_\beta(x)} = e^{\beta^T x}\]
which is the "odds" function. And taking the logarithm of both sides, we have
\[\log\Big(\dfrac{p_\beta(x)}{1-p_\beta(x)}\Big) = \beta^T x\]
which is the "log-odds" or <em>logit</em> and gives us the desired property.</p>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-6" style="background:;">
<hgroup>
<h2>The cost function</h2>
</hgroup>
<article data-timings="">
<p>\[Cost(p_\beta(x), y) =
\begin{cases}
-log(p_\beta(x)) & \text{if }y=1 \\
-log(1 - p_\beta(x)) & \text{if }y=0
\end{cases}
\]</p>
<p><img src="assets/fig/unnamed-chunk-3.png" title="plot of chunk unnamed-chunk-3" alt="plot of chunk unnamed-chunk-3" style="display: block; margin: auto;" /></p>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-7" style="background:;">
<hgroup>
<h2>The cost function</h2>
</hgroup>
<article data-timings="">
<p><br/>
We can rewrite the cost function in a simpler form as</p>
<p>\[Cost(p_\beta(x), y) = -ylog(p_\beta(x)) - (1-y)log(1-p_\beta(x))\]</p>
<p>Since when </p>
<ul>
<li>y=1 then \(Cost(p_\beta(x), y) = -log(p_\beta(x))\)<br></li>
<li>y=0 then \(Cost(p_\beta(x), y) = -log(1 - p_\beta(x))\)</li>
</ul>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-8" style="background:;">
<hgroup>
<h2>Motivation For Regularization</h2>
</hgroup>
<article data-timings="">
<p>If our \(\beta_j\)'s are unconstrained: </p>
<ul>
<li>They can explode, become very big</li>
<li>Are subject to high variance</li>
</ul>
<p>To control this variance, we can <strong>regularize</strong> these coefficients.<br>
And so we can think about this regularization in terms of the <strong>bias-variance tradeoff.</strong></p>
<p>If our \(\beta_j\)'s are subject to high variance, then we are <strong>overfitting</strong> our model to the particular quirks or noise in our dataset. So we wish to trade bias, in the form of regularization, to control this variance.</p>
<p>Not obvious that shrinking parameters does this for us.<br>
And, of course, we don't know which ones to shrink a priori!</p>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-9" style="background:;">
<hgroup>
<h2>Ridge regression</h2>
</hgroup>
<article data-timings="">
<ul>
<li><p>Recall our original logistic regression cost function to be:<br>
\[Cost(p_\beta(x), y) = -ylog(p_\beta(x)) - (1-y)log(1-p_\beta(x))\]</p></li>
<li><p>Ridge regression adds a penalty to this cost that is a function of the coefficient sizes:<br>
\[Cost_R(p_\beta(x), y) = -ylog(p_\beta(x)) - (1-y)log(1-p_\beta(x)) + \color{blue}{\lambda\sum_{j=1}^{p} \beta_j^2}\]</p></li>
<li><p>\(\lambda\) is the <strong>shrinkage parameter</strong></p>
<ul>
<li>Controls the regularization</li>
<li>\(\lambda\rightarrow0\) gives us regular logistic regression, \(\lambda\rightarrow\infty\) null model<br></li>
</ul></li>
<li><p>\(||\beta||_2 = \sum_{j=1}^{p} \beta_j^2\) is called <strong>L2 Norm</strong>. </p></li>
</ul>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-10" style="background:;">
<hgroup>
<h2>Hitters dataset from ISLR package</h2>
</hgroup>
<article data-timings="">
<pre><code class="r">Hitters <- ISLR::Hitters
dim(Hitters)
</code></pre>
<pre><code>## [1] 322 20
</code></pre>
<pre><code class="r">Hitters[1, ]
</code></pre>
<pre><code>## AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun
## -Andy Allanson 293 66 1 30 29 14 1 293 66 1
## CRuns CRBI CWalks League Division PutOuts Assists Errors
## -Andy Allanson 30 29 14 A E 446 33 20
## Salary NewLeague
## -Andy Allanson NA A
</code></pre>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-11" style="background:;">
<hgroup>
<h2>Prep data for model building</h2>
</hgroup>
<article data-timings="">
<pre><code class="r">library(ISLR)
# Remove NA
Hitters <- na.omit(ISLR::Hitters)
dim(Hitters)
</code></pre>
<pre><code>## [1] 263 20
</code></pre>
<pre><code class="r">set.seed(42)
train<-sample(1:nrow(Hitters), .6*nrow(Hitters))
test<-(-train)
# Convert Salary to a binary factor variable
Hitters$Salary <- factor(as.numeric(Hitters$Salary > 500))
</code></pre>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-12" style="background:;">
<hgroup>
<h2>Ridge regression example</h2>
</hgroup>
<article data-timings="">
<pre><code class="r">library(ISLR)
library(glmnet)
x <- model.matrix(Salary~., Hitters)[,-1]
y <- Hitters$Salary
grid=10^seq(-6,2,length=100)
ridge.mod <- glmnet(x[train,], y[train], family="binomial", alpha=0, lambda=grid)
# family="binomial" => classification, same as glm
# alpha=0 gives us the ridge regularization
# lambda is the regularization parameter
</code></pre>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-13" style="background:;">
<hgroup>
<h2>Ridge regression example</h2>
</hgroup>
<article data-timings="">
<pre><code class="r">class(ridge.mod)
</code></pre>
<pre><code>## [1] "lognet" "glmnet"
</code></pre>
<pre><code class="r">dim(coef(ridge.mod))
</code></pre>
<pre><code>## [1] 20 100
</code></pre>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-14" style="background:;">
<hgroup>
<h2>Ridge regression example</h2>
</hgroup>
<article data-timings="">
<pre><code class="r">plot(ridge.mod, xvar="lambda")
</code></pre>
<p><img src="assets/fig/unnamed-chunk-9.png" title="plot of chunk unnamed-chunk-9" alt="plot of chunk unnamed-chunk-9" style="display: block; margin: auto;" /></p>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-15" style="background:;">
<hgroup>
<h2>Choosing regularization parameter \(\lambda\)</h2>
</hgroup>
<article data-timings="">
<p>Use <strong>cross-validation</strong> to determine the appropriate \(\lambda\)</p>
<pre><code class="r">cv.ridgemod <- cv.glmnet(x[train, ], y[train], family="binomial",
alpha=0, type.measure="class", lambda=grid)
plot(cv.ridgemod)
</code></pre>
<p><img src="assets/fig/unnamed-chunk-10.png" title="plot of chunk unnamed-chunk-10" alt="plot of chunk unnamed-chunk-10" style="display: block; margin: auto;" /></p>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-16" style="background:;">
<hgroup>
<h2>Improvement over basic logistic regression?</h2>
</hgroup>
<article data-timings="">
<pre><code class="r">best_lambda <- cv.ridgemod$lambda.min
ridge.pred <- predict(ridge.mod, s=best_lambda, newx=x[test, ], type="response")
table(round(ridge.pred), y[test])
</code></pre>
<pre><code>##
## 0 1
## 0 51 19
## 1 9 27
</code></pre>
<p>for an accuracy of 0.7358. Running a plain-old logistic regression using <em>glm()</em> gives us an accuracy of 0.7264, and so the ridge regularization provides a moderate improvement in accuracy.</p>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-17" style="background:;">
<hgroup>
<h2>Lasso regression</h2>
</hgroup>
<article data-timings="">
<p><strong>L</strong>east <strong>A</strong>bsolute <strong>S</strong>hrinkage and <strong>S</strong>election <strong>O</strong>perator<br>
Coefficients can be set exactly to 0, and so it performs <em>variable selection</em><br>
This can help with interpretability, especially when # of predictors is large </p>
<p>\[Cost_L(p_\beta(x), y) = -ylog(p_\beta(x)) - (1-y)log(1-p_\beta(x)) + \color{blue}{\lambda\sum_{j=1}^{p} \left|\beta_j\right|}\]</p>
<p>\(||\beta||_1 = \sum_{j=1}^{p} \left|\beta_j\right|\) is the <strong>L1 Norm</strong><br>
Similar to ridge: </p>
<ul>
<li>\(\lambda\rightarrow0\) gives us regular logistic regression </li>
<li>\(\lambda\rightarrow\infty\) gives us null model</li>
<li>But, behavior inbetween is quite different </li>
</ul>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-18" style="background:;">
<hgroup>
<h2>Lasso regression example</h2>
</hgroup>
<article data-timings="">
<pre><code class="r">lasso.mod <- glmnet(x[train, ], y[train], lambda=grid,
family="binomial", alpha=1)
plot(lasso.mod, xvar="lambda")
</code></pre>
<p><img src="assets/fig/unnamed-chunk-13.png" title="plot of chunk unnamed-chunk-13" alt="plot of chunk unnamed-chunk-13" style="display: block; margin: auto;" /></p>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-19" style="background:;">
<hgroup>
<h2>Lasso regression example</h2>
</hgroup>
<article data-timings="">
<pre><code class="r">cv.lassomod <- cv.glmnet(x[train, ], y[train], lambda=grid,
family="binomial", alpha=1, type.measure="class")
plot(cv.lassomod)
</code></pre>
<p><img src="assets/fig/unnamed-chunk-14.png" title="plot of chunk unnamed-chunk-14" alt="plot of chunk unnamed-chunk-14" style="display: block; margin: auto;" /></p>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-20" style="background:;">
<hgroup>
<h2>Lasso performance</h2>
</hgroup>
<article data-timings="">
<pre><code class="r">lbest_lambda <- cv.lassomod$lambda.min
new.prob <- predict(lasso.mod, newx=x[test, ], s=lbest_lambda, type="response")
new.class <- round(new.prob)
table(factor(new.class), y[test])
</code></pre>
<pre><code>##
## 0 1
## 0 54 18
## 1 6 28
</code></pre>
<p>Which gives us an accuracy of 0.7736, which out-performs both the performance of the original logistic regression and the ridge regression (with accuracies of 0.7264 and 0.7358, respectively).</p>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-21" style="background:;">
<hgroup>
<h2>Model selection!</h2>
</hgroup>
<article data-timings="">
<pre><code>## 19 x 1 sparse Matrix of class "dgCMatrix"
## s0
## AtBat 0.0022191
## Hits 0.0102524
## HmRun .
## Runs .
## RBI .
## Walks 0.0195095
## Years .
## CAtBat .
## CHits 0.0018991
## CHmRun .
## CRuns .
## CRBI .
## CWalks .
## LeagueN 0.3675261
## DivisionW -0.6408992
## PutOuts 0.0007079
## Assists -0.0003869
## Errors -0.0396275
## NewLeagueN 0.2537524
</code></pre>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="" id="slide-22" style="background:;">
<hgroup>
<h2>Resources</h2>
</hgroup>
<article data-timings="">
<p><a href="http://www-bcf.usc.edu/%7Egareth/ISL/">Introduction to Statistical Learning, with applications in R</a><br>
<a href="http://web.stanford.edu/%7Ehastie/local.ftp/Springer/OLD/ESLII_print4.pdf">The Elements of Statistical Learning</a><br>
<a href="http://en.wikipedia.org/wiki/Logistic_regression">Logistic Regression</a><br>
<a href="http://statweb.stanford.edu/%7Etibs/lasso.html">The Lasso Page</a><br>
<a href="http://ss.sysu.edu.cn/%7Epy/.%5CDM%5CLecture6.pdf">Andrew Ng's Lecture Slides</a> </p>
</article>
<!-- Presenter Notes -->
</slide>
<slide class="backdrop"></slide>
</slides>
<div class="pagination pagination-small" id='io2012-ptoc' style="display:none;">
<ul>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=1 title='Overview'>
1
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=2 title='Logistic Regression'>
2
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=3 title='The logistic function'>
3
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=4 title='Logistic Regression'>
4
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=5 title='Logistic Regression'>
5
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=6 title='The cost function'>
6
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=7 title='The cost function'>
7
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=8 title='Motivation For Regularization'>
8
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=9 title='Ridge regression'>
9
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=10 title='Hitters dataset from ISLR package'>
10
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=11 title='Prep data for model building'>
11
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=12 title='Ridge regression example'>
12
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=13 title='Ridge regression example'>
13
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=14 title='Ridge regression example'>
14
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=15 title='Choosing regularization parameter \(\lambda\)'>
15
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=16 title='Improvement over basic logistic regression?'>
16
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=17 title='Lasso regression'>
17
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=18 title='Lasso regression example'>
18
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=19 title='Lasso regression example'>
19
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=20 title='Lasso performance'>
20
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=21 title='Model selection!'>
21
</a>
</li>
<li>
<a href="#" target="_self" rel='tooltip'
data-slide=22 title='Resources'>
22
</a>
</li>
</ul>
</div> <!--[if IE]>
<script
src="http://ajax.googleapis.com/ajax/libs/chrome-frame/1/CFInstall.min.js">
</script>
<script>CFInstall.check({mode: 'overlay'});</script>
<![endif]-->
</body>
<!-- Load Javascripts for Widgets -->
<script src="libraries/widgets/bootstrap/js/bootstrap.min.js"></script>
<script src="libraries/widgets/bootstrap/js/bootbox.min.js"></script>
<!-- MathJax: Fall back to local if CDN offline but local image fonts are not supported (saves >100MB) -->
<script type="text/x-mathjax-config">
MathJax.Hub.Config({
tex2jax: {
inlineMath: [['$','$'], ['\\(','\\)']],
processEscapes: true
}
});
</script>
<script type="text/javascript" src="http://cdn.mathjax.org/mathjax/2.0-latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script>
<!-- <script src="https://c328740.ssl.cf1.rackcdn.com/mathjax/2.0-latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML">
</script> -->
<script>window.MathJax || document.write('<script type="text/x-mathjax-config">MathJax.Hub.Config({"HTML-CSS":{imageFont:null}});<\/script><script src="libraries/widgets/mathjax/MathJax.js?config=TeX-AMS-MML_HTMLorMML"><\/script>')
</script>
<script>
$(function (){
$("#example").popover();
$("[rel='tooltip']").tooltip();
});
</script>
<!-- LOAD HIGHLIGHTER JS FILES -->
<script src="libraries/highlighters/highlight.js/highlight.pack.js"></script>
<script>hljs.initHighlightingOnLoad();</script>
<!-- DONE LOADING HIGHLIGHTER JS FILES -->
</html>